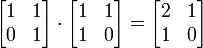Anneau commutatif

En la théorie des anneaux, une branche de l'algèbre abstraite , un anneau commutatif est un anneau dans lequel l'opération de multiplication obéit à la loi commutative . Cela signifie que si a et b sont des éléments de l'anneau, puis a × b = b × a.

L'étude des anneaux commutatifs est appelé algèbre commutative.

Exemples

• L'exemple le plus important est l' anneau des entiers avec les deux opérations d'addition et la multiplication. La multiplication ordinaire d'entiers est commutative. Cet anneau est généralement notée Z dans la littérature pour signifier le mot allemand Zahlen (numéros).
• Les rationnels , réels et complexes numéros forment anneaux commutatifs; en fait, ils sont même domaines.
• Plus généralement, tous les domaines est un anneau commutatif, donc la classe des champs est une sous-classe de la classe des anneaux commutatifs.
• Un exemple simple d'un noyau non-commutative est la ensemble de tous les deux-par-deux matrices dont les entrées sont des nombres réels. Par exemple, la multiplication matricielle

ne est pas égal à la multiplication effectuée dans l'ordre inverse:

• Si n est un entier positif, alors l'ensemble Z des entiers modulo _n n forme un anneau commutatif à n éléments (voir arithmétique modulaire ).
• Si R est un anneau commutatif donné, alors l'ensemble de tous les polynômes de la variable X dont les coefficients sont dans la R forme un nouveau anneau commutatif, noté R [X].
• De même, l'ensemble de séries formelles R [[X _1, ..., X _n]] sur un anneau commutatif R est un anneau commutatif. Si R est un champ, l'anneau de séries formelles de puissance est un type spécial d'anneau commutatif, appelé complet anneau local.
• L'ensemble des nombres rationnels ordinaires dont le dénominateur est formes bizarres un anneau commutatif, en fait un anneau local. Cet anneau contient l'anneau des entiers correctement, et est lui-même un sous-ensemble du champ rationnel.
• Si p est tout nombre premier , l'ensemble des p entiers -adiques forme un anneau commutatif.
• Un ensemble de matrices qui peuvent être diagonalisée avec le même transformation similitude forme un anneau commutatif. Un exemple est l'ensemble des matrices de différences divisées par rapport à un ensemble fixe de nœuds.

Construire anneaux commutatifs

Étant donné un anneau commutatif, on peut l'utiliser pour construire de nouveaux anneaux, comme décrit ci-dessous.

• anneau de Factor: Étant donné un anneau commutatif R et une idéal I de R, le anneau de facteur R / I est l'ensemble des classes à de I avec les opérations (A + i) + (B + I) = (a + b) + I et (a + I) (b + I) = ab + I .
• Localisation: Si S est un partie multiplicative d'un anneau commutatif R alors nous pouvons définir la localisation de R à S, ou un anneau de fractions avec des dénominateurs dans S, généralement notée S ^-1 R. L'exemple ci-dessus avant-dernier est la localisation de l'anneau des entiers à la partie multiplicative des nombres impairs. Le corps des rationnels est la localisation de l'anneau commutatif d'entiers à l'ensemble multiplicatif des entiers non nuls.
• Achèvement: Si I est un idéal d'un anneau commutatif R, les pouvoirs de I forment des quartiers topologiques de 0 qui permettent R pour être considéré comme un anneau topologique. Cette topologie est appelée la topologie I-adique. R peut alors être complété par rapport à cette topologie. Formellement, l'achèvement -adique I est le limite projective des anneaux R / I ^n. Par exemple, si k est un corps, k [[X]], le formelle anneau de série de puissances d'une variable sur k, est l'achèvement -adique I de k [X] où I est l'idéal principal engendré par X. De manière analogue, l'anneau des entiers de p -adiques est l'achèvement -adique I de Z où I est l'idéal principal engendré par p.
• Si R est un anneau commutatif donné, l'ensemble de tous les polynômes R [X _1, ..., X _n] sur R forme un nouveau anneau commutatif, appelé anneau de polynômes en n variables sur R.
• Si R est un anneau commutatif donné, alors l'ensemble de tous séries formelles R [[X _1, ..., X _n]] sur un anneau commutatif R est un anneau commutatif, appelé l'anneau de série de puissances de n variables sur R.

Propriétés

• Tous sous-anneaux et anneaux quotients des anneaux commutatifs sont également commutative.
• Si f: R → S est un injective homomorphisme d'anneaux (ce est un monomorphism) entre les anneaux R et S, et si S est commutatif, alors R doit également être commutative, puisque f (a · b) = f (a) · f (b) = f (b) · f (a) = f (b · a).
• De même, si f: R → S est un homomorphisme d'anneaux entre les anneaux R et S, et si R est commutatif, le sous-anneau f (R) S est également commutative; en particulier, si f est surjective (et donc un épimorphisme), S doit être commutative.
• Chaque finie Corps est commutative ( Le théorème de Wedderburn). N. Jacobson a montré que la condition suivante est suffisante: si R est un cycle tel que, pour chaque élément x de R, il existe un nombre entier n> 1 de telle sorte que x = x ^n, alors R est commutatif. Des conditions beaucoup plus générales qui garantissent la commutativité d'un anneau ont ensuite été découvert par EN Herstein et autres.

Discussion générale

La structure interne d'un anneau commutatif est déterminée en considérant ses idéaux. Tous les idéaux dans un anneau commutatif sont recto-verso, ce qui simplifie considérablement la situation.

La structure extérieure d'un anneau commutatif est déterminée en considérant l'algèbre linéaire sur cet anneau, ce est à dire, en enquêtant sur la théorie de son modules. Ce sujet est beaucoup plus difficile lorsque l'anneau commutatif ne est pas un champ et est généralement appelé algèbre homologique. L'ensemble des idéaux dans un anneau commutatif R peut être caractérisée exactement comme l'ensemble des -modules R qui sont sous-modules de R.

Un élément a d'un anneau commutatif (l'identité) est appelé unité si elle possède un inverse multiplicatif, ce est à dire, se il existe un autre élément b de l'anneau (avec b pas nécessairement distincte d'une) de sorte que ab = 1. Chaque élément non nul d'un champ est une unité. Chaque élément d'un anneau commutatif locale ne figure pas dans l'idéal maximal est une unité.

Un élément non nul a d'un anneau commutatif est dit être un Diviseur de zéro se il existe un élément non nul b de l'anneau de telle sorte que ab = 0. Un anneau commutatif avec l'identité qui possède pas de diviseurs zéro est appelé domaine intégrante car elle ressemble étroitement les entiers à certains égards.

Certains des types spécifiques d'anneaux commutatifs sont donnés avec la chaîne d'inclusions suivantes:

anneaux commutatifs ⊃ intègres ⊃ domaines de factorisation uniques ⊃ principaux domaines idéales ⊃ Domaines euclidiens ⊃ champs

Une autre chaîne possible (ce qui est plus géométrique) est la chaîne d'inclusions suivantes:

Cohen-Macaulay anneaux ⊃ Anneaux Gorenstein ⊃ Anneaux réguliers ⊃ Anneaux locaux réguliers