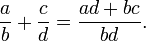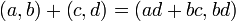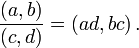Nombre rationnel

À propos de ce écoles sélection Wikipedia

Cette sélection écoles a été choisi par SOS Enfants pour les écoles dans le monde en développement ne ont pas accès à Internet. Il est disponible en téléchargement intranet. Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

En mathématiques , un nombre rationnel est un nombre qui peut être exprimé en tant que rapport de deux nombres entiers . Non entières des nombres rationnels (communément appelés des fractions ) sont généralement écrits comme fraction vulgaire 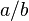$a / b$ , Où b ne est pas zéro . un est appelé le numérateur , et B du dénominateur .

Chaque nombre rationnel peut être écrit en une infinité de formes, telles que 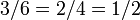$3/6 = 2/4 = 1/2$ , Mais il est dit d'être en forme la plus simple lorsque A et B ne ont pas communs diviseurs sauf 1 (ce est à dire, ils sont premiers entre eux). Chaque nombre rationnel non nul a exactement une forme la plus simple de ce type avec un dénominateur positif. Une fraction de cette forme la plus simple est dit être un fraction irréductible, ou d'une fraction sous forme réduite.

Le développement décimal d'un nombre rationnel est éventuellement périodique (dans le cas d'une extension finie les zéros qui suivent implicitement forment la partie périodique). Le même est vrai pour toute autre base intégrale ci-dessus un, et ce est également vrai lorsque des nombres rationnels sont considérés comme nombres p-adiques plutôt que des nombres réels . En revanche, si l'expansion d'un nombre de base est une périodiquement, il est périodique à toutes les bases et le nombre est rationnel. Un nombre réel qui ne est pas un nombre rationnel est appelé un nombre irrationnel .

Quarters

Le ensemble de tous les nombres rationnels, qui constitue une terrain, est notée 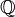$\ Mathbb {Q}$ . En utilisant le notation set-constructeur, 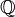$\ Mathbb {Q}$ est défini comme étant

$\ Mathbb {Q} = \ \ left {\ frac {m} {n}: m \ in \ mathbb {Z}, n \ in \ mathbb {Z}, n \ ne 0 \ right \},$

où $\ Mathbb {Z}$ désigne l'ensemble des entiers.

Le terme rationnelle

Dans le monde mathématique, l'adjectif rationnelle signifie souvent que le sous-jacent domaine considéré est le champ 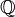$\ Mathbb {Q}$ numéros de rationnels. Par exemple, un nombre entier rationnel est un algébrique entier qui est également un nombre rationnel, ce est-à-dire un nombre entier ordinaire, et un rationnelle matrice est une matrice dont les coefficients sont des nombres rationnels. Polynomiale rationnelle habituellement, et le plus correctement, signifie un polynôme à coefficients rationnels, également appelé "polynomiale sur les rationnels". Cependant, fonction rationnelle ne signifie pas que le champ sous-jacent est les nombres rationnels, et un courbe algébrique rationnelle ne est pas une courbe algébrique à coefficients rationnels.

Arithmétique

Deux nombres rationnels 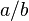$a / b$ et $c / d$ sont égaux si et seulement si $ad = bc$ .

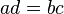Deux fractions sont ajoutés comme suit

$\ Frac {a} {b} + \ frac {c} {d} = \ frac {ad + bc} {} bd.$

La règle pour la multiplication est

$\ Frac {a} {b} \ cdot \ frac {c} {d} = \ frac {} {ac bd}.$

Additif et inverses multiplicatifs existent dans les nombres rationnels

$- \ Left (\ frac {a} {b} \ right) = \ frac {-a} {b} = \ frac {a} {- b} \ quad \ mbox {et} \ quad \ gauche (\ frac { a} {b} \ right) ^ {- 1} = \ frac {b} {a} \ mbox {if} a \ neq 0.$

Il en résulte que le quotient de deux fractions est donnée par

$\ Frac {a} {b} \ div \ frac {c} {d} = \ frac {} {ad bc}.$

Fractions égyptiennes

Ne importe quel nombre rationnel positif peut être exprimée comme une somme de distincte inverses des nombres entiers positifs, tels que

$\ Frac {5} {7} = \ frac {1} {2} + \ frac {1} {6} + \ frac {1} {21}.$

Pour tout nombre rationnel positif, il ya une infinité de telles représentations différentes, appelées Fractions égyptiennes, car ils ont été utilisés par l'ancienne Égyptiens. Les Egyptiens avaient également une notation différente pour fractions dyadique.

Construction formelle

Mathématiquement, nous pouvons construire les nombres rationnels comme classes d'équivalence de paires ordonnées de nombres entiers 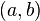$\ Left (a, b \ right)$ Avec $b$ pas égal à zéro. Nous pouvons définir addition et la multiplication de ces paires avec les règles suivantes:

$\ Left (a, b \ right) + \ left (c, d \ right) = \ left (ad + bc, bd \ right)$

$\ Left (a, b \ droite) \ times \ left (c, d \ right) = \ left (AC, BD \ right)$

et si c ≠ 0, la division par

$\ Frac {\ left (a, b \ right)} {\ left (c, d \ right)} = \ left (AD, BC \ right).$

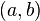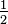L'intuition est que $\ Left (a, b \ right)$ représente le nombre désigné par la fraction $\ Frac {a} {b}.$ Pour se conformer à notre attente que $\ Frac {2} {4}$ et $\ Frac {1} {2}$ désigner le même nombre, nous définissons une relation d'équivalence $\ Sim$ sur ces paires avec la règle suivante:

$\ Left (a, b \ right) \ sim \ left (c, d \ right) \ mbox {si et seulement si} ad = bc.$

Cette relation d'équivalence est une relation de congruence: il est compatible avec l'addition et la multiplication défini ci-dessus, et l'on peut définir comme la Q ensemble de ~ du quotient, ce est à dire nous identifions deux paires (a, b) et (c, d) si elles sont équivalentes au sens ci-dessus. (Cette construction peut être réalisée dans ne importe quel domaine intégrante: voir corps des fractions.)

Nous pouvons également définir une ordre total sur Q par écrit

$\ Left (a, b \ right) \ le \ left (c, d \ right) \ mbox {if} (bd> 0 \ mbox {et} ad \ le bc) \ mbox {ou} (bd <0 \ mbox {et} ad \ ge bc).$

Les entiers peuvent être considérés comme des nombres rationnels de la intégration que les cartes $p \,$ à $[(P, 1)], \,$ où $[(A, b)] \,$ désigne la classe d'équivalence ayant $(A, b) \,$ en tant que membre.

Propriétés

un schéma illustrant le countabililty des rationnels

L'ensemble 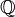$\ Mathbb {Q}$ , Ainsi que les opérations d'addition et de multiplication ci-dessus, forme un domaine, la domaine de fractions des nombres entiers $\ Mathbb {Z}$ .

Les rationnels sont le plus petit champ avec caractéristique nulle: tous les autres corps de caractéristique nulle contient une copie du 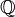$\ Mathbb {Q}$ . Les nombres rationnels sont donc le terrain de choix pour caractéristique zéro.

Le clôture algébrique de 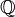$\ Mathbb {Q}$ , Ce est à dire le domaine de racines de polynômes rationnels, ce est le nombres algébriques.

L'ensemble des nombres rationnels est dénombrable. Depuis l'ensemble des nombres réels est incalculable, nous disons que presque tous les nombres réels sont irrationnels, dans le sens de Mesure de Lebesgue, ce est à dire l'ensemble des nombres rationnels est un ensemble vide.

Les rationnels sont un densément commandé jeu: entre deux rationnels, il est assis un de l'autre, en fait une infinité de autres. Tout totalement ordonné ensemble qui est dénombrable, dense (au sens ci-dessus), et ne comporte aucun élément moins ou plus est isomorphe à commander les nombres rationnels.

Nombres réels et les propriétés topologiques des rationnels

Les rationnels sont un sous-ensemble dense des nombres réels: tout nombre réel a nombres rationnels arbitraire qui lui sont proches. Une propriété connexe est que des nombres rationnels sont les seuls numéros avec expansions finis que fractions continues régulières.

En vertu de leur ordre, les rationnels portent une Afin topologie. Les nombres rationnels portent également une Topologie induite. Les nombres rationnels forment un espace métrique en utilisant la distance d (x, y) = | x - y |, et on obtient une troisième topologie sur 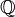$\ Mathbb {Q}$ . Tous les trois topologies coïncident et tourner les rationnels dans un champ topologique. Les nombres rationnels sont un exemple important d'un espace qui ne est pas localement compact. Les rationnels se caractérisent topologiquement comme uniques dénombrable espace métrisable sans points isolés. L'espace est également totalement déconnecté. 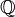Les nombres rationnels ne forment pas un compléter espace métrique; les nombres réels sont l'achèvement de $\ Mathbb {Q}$ .

p numéros -adiques

En plus de la mesure absolue de la valeur mentionnée ci-dessus, il existe d'autres paramètres qui tournent 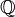$\ Mathbb {Q}$ dans un champ topologique:

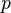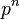Laisser $p$ être un nombre premier , et pour tout entier non nul $une$ laisser $| A | _p = p ^ {- n}$ Où $p ^ n$ est la plus grande puissance de 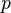$p$ partage $une$ ;

En outre écriture 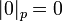$| 0 | _p = 0$ . Pour tout nombre rationnel $\ Frac {a} {b}$ , Nous avons mis en $\ Left | \ frac {a} {b} \ right | _p = \ frac {| a | _p} {| b | _p}$ .

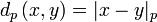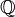Puis $D_P \ left (x, y \ right) = | x - y | _p$ définit un sur métrique $\ Mathbb {Q}$ .

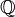L'espace métrique $\ Left (\ mathbb {Q}, D_P \ right)$ ne est pas complète, et son achèvement est le p champ de numéro -adique $\ Mathbb {Q} _p$ . Théorème d'Ostrowski stipule que toute non-trivial valeur absolue sur les nombres rationnels $\ Mathbb {Q}$ est équivalente à la valeur absolue soit réel ou habituel un p-adique valeur absolue.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Rational_number&oldid=199219044 "

Privacy Policy and Contacts (IT)