
Curl (mathématiques)
À propos de ce écoles sélection Wikipedia
SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . Avec enfants SOS vous pouvez choisir de parrainer des enfants dans plus de cent pays
Dans le calcul vectoriel , boucle (ou: rotor) est un opérateur vectoriel qui montre un «Le taux de de champ de vecteurs rotation », ce est-à la direction de l'axe de rotation et la amplitude de la rotation. Il peut également être décrit comme le la densité de la circulation.
"Rotation" et "circulation" sont utilisés ici pour propriétés d'une fonction de vecteur de la position, indépendamment de leur éventuel changement dans le temps.
Un champ de vecteurs qui a courbure nulle partout est appelé irrotationnel.
Le rotor de la terminologie alternatif et autre notation (utilisé dans de nombreux pays européens) est  sont souvent utilisés pour friser et
sont souvent utilisés pour friser et  .
.
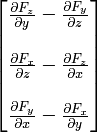
Coordonner-invariant Définition comme une densité de circulation
Le composant de  dans la direction du vecteur unitaire
dans la direction du vecteur unitaire  est la limite d'une intégrale de ligne par unité de surface de
est la limite d'une intégrale de ligne par unité de surface de  , À savoir l'intégrale ci-après la courbe fermée
, À savoir l'intégrale ci-après la courbe fermée 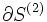 . Cette courbe fermée est dans un plan normal à
. Cette courbe fermée est dans un plan normal à  :
:
Maintenant pour calculer les composants de  par exemple en coordonnées cartésiennes , remplacer
par exemple en coordonnées cartésiennes , remplacer  avec des vecteurs unitaires i, j et k.
avec des vecteurs unitaires i, j et k.
Ceci définit non seulement la courbure d'une manière libre de tout coordonnées, mais rend également visible que ce est une densité de circulation.
Le théorème de Stokes (voir ci-dessous) peut être directement dérivée de celle-ci et de la représentation en coordonnées spéciaux peut être explicitement obtenu.
Usage
En mathématiques la boucle est défini comme:
où F est le champ de vecteurs de la boucle qui est appliquée. Bien que la version sur la droite est strictement un abus de notation, il est toujours utile en tant que mnemonic si nous prenons  comme vecteur opérateur différentiel del ou nabla. Cette notation impliquant opérateurs est courante dans la physique et l'algèbre .
comme vecteur opérateur différentiel del ou nabla. Cette notation impliquant opérateurs est courante dans la physique et l'algèbre .
Élargi en coordonnées cartésiennes , 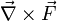 est, par F composé de [F x, F y, F z]:
est, par F composé de [F x, F y, F z]:
Bien exprimée en termes de coordonnées, le résultat est invariante par rotation appropriée des axes de coordonnées, mais le résultat inverse en réflexion.
Un simple représentation de la forme élargie de la boucle est:
ce est-del transversale F, ou que le déterminant de la matrice suivante:
où i, j, et k sont le vecteurs unitaires pour la x -, y et z - -axes, respectivement.
En Notation Einstein, avec le Symbole de Levi-Civita il est écrit que:
ou en tant que:
pour les vecteurs unitaires:  , K = 1,2,3 correspondant à
, K = 1,2,3 correspondant à  Et
Et  respectivement.
respectivement.
En utilisant le dérivée extérieure, il est écrit simplement:
En prenant la dérivée extérieur d'un champ de vecteurs ne aboutit pas à un autre champ vectoriel, mais un 2-forme ou champ bivecteur, bien écrit 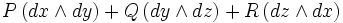 .
.
Depuis bivecteurs sont généralement considérés comme moins intuitive que vecteurs ordinaires, le R ³- double:  est couramment utilisé à la place (où
est couramment utilisé à la place (où  désigne le Hodge opérateur étoiles). C'est un chiral fonctionnement, produisant un pseudovector qui prend des valeurs opposées dans la main gauche et la main droite les systèmes de coordonnées.
désigne le Hodge opérateur étoiles). C'est un chiral fonctionnement, produisant un pseudovector qui prend des valeurs opposées dans la main gauche et la main droite les systèmes de coordonnées.
Interprétation de la boucle
La boucle du champ de vecteurs nous parle de la rotation, le champ a à tout moment. L'ampleur de la boucle nous dit combien il est rotation. La direction nous dit, par le Règle de la main droite (quatre doigts de la main droite sont bouclés dans le sens de la motion et le pouce dans la direction de la rotation) dont l'axe le domaine est en rotation.
Un dispositif couramment utilisé pour penser à friser est la roue à aubes. Si nous devions placer une très petite roue à aubes à un point dans le champ de vecteurs en question et de traiter les vecteurs dessinés et leurs longueurs que les courants dans une rivière avec grandeur et la direction, de quelque côté que la roue à aubes aurait tendance à tourner est la direction de la boucle à ce point. Par exemple, si deux courants tentent de faire tourner la roue dans des directions opposées, l'une plus forte (le vecteur plus) va gagner.
Exemples
Un champ de vecteurs simples
Prenez le champ de vecteurs construit en utilisant vecteurs unitaires
 .
.
Son intrigue ressemble à ceci:

Simplement en inspection visuelle, nous pouvons voir que le domaine est en rotation. Si nous nous en tenons une roue à aubes ne importe où, on voit immédiatement sa tendance à tourner vers la droite. En utilisant le Règle de la main droite, nous nous attendons à la boucle soit dans la page. Si nous voulons garder un droitier système de coordonnées, dans la page sera dans la direction z négative.
Si nous faisons le calcul et trouvons la boucle:
Ce est en effet dans la direction z négative, comme prévu. Dans ce cas, la boucle est en fait une constante, indépendamment de la position. La «quantité» de rotation dans le champ de vecteurs ci-dessus est la même en tout point (x, y). Tracé de la boucle de F ne est pas très intéressant:

Un exemple plus complet
Supposons que nous considérons maintenant un champ de vecteurs légèrement plus compliquée:
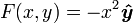 .
.
Son intrigue:
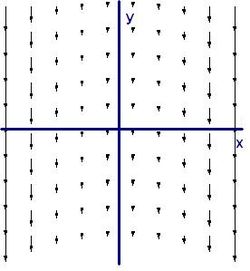
Nous pourrions ne pas voir toute rotation au départ, mais si nous regardons de près le droit, nous voyons un champ plus large, disons, x = 4 qu'à x = 3. Intuitivement, si nous avons placé une petite roue à aubes là, le plus grand "courant" sur le côté droit causerait la roue à aubes de tourner dans le sens horaire, ce qui correspond à une boucle dans le sens de z négative. En revanche, si nous regardons un point sur la gauche et a placé une petite roue à aubes là, le plus grand "courant" sur le côté gauche causerait la roue à aubes de tourner dans le sens antihoraire, ce qui correspond à une boucle dans le sens de z positif. Nous allons vérifier notre hypothèse en faisant le calcul:
En effet, la boucle se trouve dans la direction z pour x positif et négatif dans la direction z négative pour x positifs, comme prévu. Depuis cette boucle ne est pas le même à chaque point, son intrigue est un peu plus intéressant:

Nous notons que l'intrigue de cette boucle n'a pas de dépendance sur y ou z (comme il ne devrait pas) et est dans la direction z négative pour x positives et dans la direction z positive pour x négatif.
Trois exemples courants
Prenons l'exemple ∇ × [v × F]. Utilisation de coordonnées cartésiennes, on peut montrer que
Dans le cas où le v de champ de vecteur et ∇ sont interchangeables:
qui introduit la notation de l'Feynman ∇ F, ce qui signifie le gradient indicé fonctionne uniquement sur le facteur F.
Un autre exemple est ∇ × [∇ × F]. En coordonnées cartésiennes, il peut être démontré que:
qui, avec un peu de casse-tête, peut être interprété comme un cas particulier du premier exemple avec la substitution v → ∇.
Exemples descriptives
- Dans une tornade les vents tournant autour de l'œil, et un champ de vecteurs montrant des vitesses de vent auraient une boucle non-zéro à l'œil, et peut-être ailleurs (voir tourbillon).
- Dans un champ de vecteurs, qui décrit les vitesses linéaires de chaque partie individuelle d'un disque tournant, la boucle aura une valeur constante sur toutes les parties du disque.
- Si les vitesses de voitures sur une autoroute ont été décrit avec un champ de vecteurs et les voies eu des limitations de vitesse différentes, la boucle sur les frontières entre les voies serait non nulle.
- La loi de Faraday de l'induction, l'une des équations de Maxwell , peut être exprimée très simplement en utilisant boucle. Il indique que la boucle d'un champ électrique est égal à l'inverse du taux de temps de changement du champ magnétique.
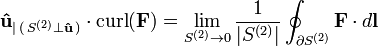

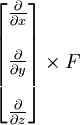


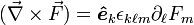

![\ Vec {\ nabla} \ times \ vec {F} = 0 \ boldsymbol {\ hat {x}} + 0 \ boldsymbol {\ hat {y}} + [{\ frac {\ partial} {\ x partielle}} (-x) - {\ frac {\ partial} {\ y partielle}} y] \ boldsymbol {\ hat {z}} = - 2 \ boldsymbol {\ hat {z}}](../../images/203/20399.png)

![\ Mathbf {\ nabla \ fois} \ left (\ mathbf {v \ times F} \ right) = \ left [\ left (\ mathbf {\ nabla \ cdot F} \ right) + \ mathbf {F \ cdot \ nabla } \ right] \ mathbf {v} - \ left [\ left (\ mathbf {\ nabla \ cdot c} \ right) + \ mathbf {v \ cdot \ nabla} \ right] \ mathbf {F} \.](../../images/204/20414.png)


