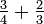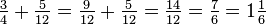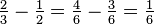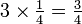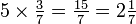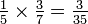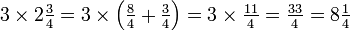Fraction (mathématiques)
À propos de ce écoles sélection Wikipedia
SOS Enfants, qui se déroule près de 200 sos écoles dans le monde en développement, a organisé cette sélection. SOS Enfants a regardé des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?

En mathématiques , une fraction (du latin fractus, cassé) est un concept d'une proportionnelle relation entre une partie de l'objet et l'objet entier. Chaque fraction est constituée d'un dénominateur (en bas) et un numérateur (en haut), soit (respectivement) le nombre de parties égales que l'objet est divisé en, et le nombre de ces pièces indiquées pour la fraction particulière.
Pour exemple, la fraction ¾ pourrait être utilisé pour représenter trois parties égales d'un objet entier, si elle était divisée en quatre parties égales. Parce qu'il est impossible de diviser quelque chose dans zéro parties égales, nulle ne peut jamais être le dénominateur d'une fraction (voir division par zéro). Une fraction avec une égale numérateur et le dénominateur est égale à une (par exemple 5/5 = 1) et la forme de fraction est rarement, sinon jamais, donné comme résultat final.
Une fraction est un exemple d'un type spécifique de rapport, dans lequel les deux nombres sont liées dans une relation partie à tout, plutôt que comme un rapport comparatif entre deux quantités séparées. Une fraction est un quotient de nombres , la quantité obtenue lorsque le numérateur est divisé par le dénominateur. Ainsi ¾ représente trois divisé par quatre, en décimales 0,75, un pourcentage de 75%. Les trois parties égales du gâteau sont 75% de l'ensemble du gâteau.
En mathématiques supérieures, une fraction est considérée comme un élément d'une corps des fractions.
Historiquement, un certain nombre qui ne représente pas l'ensemble a été appelé un "fraction". Les chiffres que nous appelons aujourd'hui «décimales» ont été à l'origine appelé "les fractions décimales"; les chiffres que nous appelons aujourd'hui «fractions» étaient appelés «fractions vulgaires», le mot «vulgaire» signifie «monnaie courante».
Le numérateur et le dénominateur d'une fraction peuvent être séparés par une ligne oblique appelée solidus ou slash, par exemple ¾, ou peut être écrit ci-dessus et au-dessous d'une ligne horizontale appelé vinculum, ainsi:  .
.
Le solidus peut être omise dans le style inclinée (par exemple de 3 4) où l'espace est courte et le sens est évident à partir du contexte, par exemple dans panneaux de signalisation dans certains pays.
Les fractions sont utilisés le plus souvent lorsque le dénominateur est relativement faible. Il est plus facile de multiplier par 32 3/16 que de faire le même calcul en utilisant équivalent décimal de la fraction (0,1875). Il est également plus précise de multiplier par 15 ⅓, par exemple, que ce est à multiplier par 15 une approximation décimale d'un tiers. Pour changer une fraction d'un nombre décimal, il faut diviser le numérateur par le dénominateur, et arrondir à la précision souhaitée.
Les fractions sont également des nombres rationnels, en ce qui signifie que le dénominateur et le numérateur sont des nombres entiers.
Le mot est aussi utilisé dans les expressions connexes, tels que fraction continue et algébrique fraction voir Cas particuliers ci-dessous.
Les formes de fractions
Vulgaire, bonne, et des fractions impropres
Une fraction vulgaire (ou fraction libre) est un nombre rationnel écrit comme une nombre entier (numérateur) divisé par un nombre entier non nul (dénominateur), par exemple, 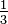 ,
,  et
et  .
.
Une fraction vulgaire est dit être une fraction appropriée si la valeur absolue du numérateur est inférieure à la valeur absolue du dénominateur qui est, si la valeur absolue de la totalité de la fraction est inférieure à 1 (par exemple,  ), Mais une fraction impropre (US, britannique ou australien) ou top-heavy fraction (Colombie uniquement) si la valeur absolue du numérateur est supérieur ou égal à la valeur absolue du dénominateur (par exemple,
), Mais une fraction impropre (US, britannique ou australien) ou top-heavy fraction (Colombie uniquement) si la valeur absolue du numérateur est supérieur ou égal à la valeur absolue du dénominateur (par exemple,  ).
).
Nombres fractionnaires
Un nombre fractionnaire est la somme d'un nombre entier et d'une fraction correspondant. Par exemple, en se référant à deux galettes entières et les trois quarts d'un autre gâteau, l'ensemble et des parties fractionnaires de nombre sont écrites côté de l'autre: 2 + 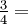 2
2  .
.
Une fraction impropre peut être considéré comme une autre façon d'écrire un nombre mixte; dans le "2  "Exemple ci-dessus, imaginez que les deux gâteaux entiers sont chacun divisés en quarts. Chacun contribue à gâteaux entiers
"Exemple ci-dessus, imaginez que les deux gâteaux entiers sont chacun divisés en quarts. Chacun contribue à gâteaux entiers 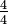 au total, de sorte
au total, de sorte 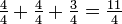 est une autre façon d'écrire 2
est une autre façon d'écrire 2  .
.
Un certain nombre mixte peut être converti en une fraction impropre en trois étapes:
- Multiplier la partie entière par le dénominateur de la partie fractionnaire.
- Ajouter le numérateur de la fraction à ce produit.
- La somme résultante est le numérateur de la nouvelle (incorrect) fraction, et le nouveau dénominateur est le même que celui de la partie fractionnaire du nombre fractionnaire.
De même, une fraction impropre peut être convertie en un nombre mixte:
- Diviser le numérateur par le dénominateur.
- Le quotient (sans reste) devient toute la partie et le reste devient le numérateur de la fraction.
- Le nouveau dénominateur est la même que celle de l'expression fractionnaire d'origine.
Fractions équivalentes
Multipliant le numérateur et le dénominateur d'une fraction par les mêmes résultats (non nulle) Numéro dans une nouvelle fraction qui est dit être équivalent à la fraction originale. Le mot équivalent signifie que les deux fractions ont la même valeur. Ce est vrai parce que pour ne importe quel nombre 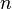 , En multipliant par
, En multipliant par  est vraiment en multipliant par un, et ne importe quel nombre multiplié par une a la même valeur que le numéro d'origine. Par exemple, considérons la fraction
est vraiment en multipliant par un, et ne importe quel nombre multiplié par une a la même valeur que le numéro d'origine. Par exemple, considérons la fraction 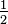 : Lorsque le numérateur et le dénominateur sont multipliées par deux à la fois, le résultat est
: Lorsque le numérateur et le dénominateur sont multipliées par deux à la fois, le résultat est  , Qui a la même valeur (0,5) en tant que
, Qui a la même valeur (0,5) en tant que 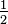 . Pour cette image visuelle, imaginez coupe l'exemple gâteau en quatre morceaux; deux des pièces ensemble (
. Pour cette image visuelle, imaginez coupe l'exemple gâteau en quatre morceaux; deux des pièces ensemble (  ) Représentent la moitié du gâteau (
) Représentent la moitié du gâteau ( 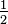 ).
).
Par exemple: 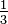 ,
, 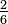 ,
, 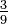 et
et 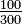 sont tous des fractions équivalentes.
sont tous des fractions équivalentes.
Divisant le numérateur et le dénominateur d'une fraction par le même nombre non nul permettra également d'obtenir une fraction équivalente. ce est ce qu'on appelle la réduction ou la simplification de la fraction. Une fraction dont le numérateur et le dénominateur ne ont pas de facteurs en commun (sauf une) est dit irréductible ou dans ses termes les plus faibles ou les plus simples. Par exemple, 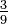 ne est pas en termes plus bas parce que les deux 3 et 9 peuvent être exactement divisé par 3. En revanche,
ne est pas en termes plus bas parce que les deux 3 et 9 peuvent être exactement divisé par 3. En revanche, 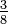 est plus faible en termes, le seul nombre qui est à la fois un facteur de 3 et la figure 8 est une.
est plus faible en termes, le seul nombre qui est à la fois un facteur de 3 et la figure 8 est une.
Inverses et le «dénominateur invisible"
Le réciproque d'une fraction est une autre fraction avec le numérateur et le dénominateur inverse. L'inverse de 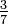 , Par exemple, est
, Par exemple, est 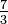 .
.
Étant donné que ne importe quel nombre divisé par une résultats dans le même numéro, il est possible d'écrire ne importe quel nombre entier en tant que fraction en utilisant comme dénominateur 1: 17 =  (1 est parfois appelé le «dénominateur invisible»). Par conséquent, sauf pour le zéro, chaque fraction ou nombre entier a une réciproque. L'inverse de 17 serait
(1 est parfois appelé le «dénominateur invisible»). Par conséquent, sauf pour le zéro, chaque fraction ou nombre entier a une réciproque. L'inverse de 17 serait  .
.
Fractions complexes
Une fraction complexe (ou fraction de composé) est une fraction dont le numérateur et le dénominateur comprend une fraction. Par exemple, 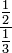 est une fraction complexe. Pour simplifier une fraction complexe, divisez le numérateur par le dénominateur, comme dans toute autre fraction:
est une fraction complexe. Pour simplifier une fraction complexe, divisez le numérateur par le dénominateur, comme dans toute autre fraction:  .
.
Arithmétique avec des fractions
Fractions, comme des nombres entiers, obéissent à la commutative , associative , et lois de distribution, et la règle contre la division par zéro.
Comparant des fractions
Comparant des fractions ayant le même dénominateur ne nécessite comparant les numérateurs.
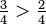 comme
comme  .
.
Afin de comparer des fractions avec des dénominateurs différents, ceux-ci sont convertis à un dénominateur commun: pour comparer  et
et 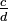 , Ceux-ci sont convertis en
, Ceux-ci sont convertis en 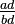 et
et 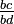 Où bd est le produit des dénominateurs, puis l'numérateurs AD et BC sont comparées.
Où bd est le produit des dénominateurs, puis l'numérateurs AD et BC sont comparées.
 ?
? 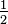 donne
donne 
Ce procédé est également connu comme le procédé "cross-multiply" qui se explique en multipliant le nombre supérieure et inférieure opposées. Le produit des dénominateurs est utilisé comme (le moins fréquent, mais pas nécessaire) dénominateur commun.
 ?
? 
Multipliez 17 par 5 et 18 par 4. Placer les produits des équations sur le dessus des dénominateurs. Le plus grand nombre identifie la fraction la plus importante. Donc 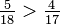 que 17 × 5 = 85 est supérieur à 18 × 4 = 72.
que 17 × 5 = 85 est supérieur à 18 × 4 = 72.
Afin de travailler avec de plus petits nombres, le dénominateur commun est utilisé à la place du produit. Les fractions sont convertis en fractions avec le plus petit dénominateur commun, et alors les numérateurs sont comparées.
 ?
?  donne
donne 
Certains textes basés sur des normes de mathématiques tels que Mathématiques connectés omettre l'instruction de dénominateurs communs les moins entièrement. Ce texte présente l'utilisation des «bandes» (une fraction de la bande de papier pliée en fractions fractions) ou "de référence", tels que la moitié contre laquelle une fraction telle que les deux cinquièmes peuvent être comparés. Bien que ces méthodes peuvent être utiles pour renforcer la compréhension conceptuelle, ils sont controversées car elles ne sont pas efficaces au-delà du niveau de l'école élémentaire, et ces textes sont souvent complétés par des enseignants à la méthode standard.
Addition
La première règle de l'addition est que seulement comme quantités peuvent être ajoutées; par exemple, diverses quantités de quarts. Contrairement quantités, telles que l'ajout tiers aux trimestres, doit d'abord être converti en voulez quantités comme décrit ci-dessous:
Ajout comme quantités
Imaginez une poche contenant deux trimestres, et une autre poche contenant trois quarts; au total, il ya cinq trimestres. Depuis quatre quarts est équivalente à une (dollar), ce qui peut être représentée comme suit:
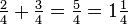 .
.

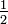 d'un gâteau, doit être ajouté à
d'un gâteau, doit être ajouté à  d'un gâteau, les pièces doivent être convertis en quantités comparables, tels que gâteaux huitièmes ou gâteau quarts.
d'un gâteau, les pièces doivent être convertis en quantités comparables, tels que gâteaux huitièmes ou gâteau quarts. Ajout contrairement quantités
Pour ajouter fractions contenant contrairement quantités (par exemple, les quarts et les tiers), il est nécessaire de convertir tous les montants à aimer quantités. Il est facile de travailler sur le type de fraction convertir; il suffit de multiplier ainsi les deux dénominateurs (nombre en bas) de chaque fraction.
Pour ajouter des quarts de tiers, les deux types de fraction sont convertis en  (douzièmes).
(douzièmes).
Pensez à ajouter les deux quantités suivantes:
Premièrement, convertir  en douzièmes en multipliant le numérateur et le dénominateur par trois:
en douzièmes en multipliant le numérateur et le dénominateur par trois: 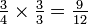 . Notez que
. Notez que  est équivalent à 1, ce qui montre que
est équivalent à 1, ce qui montre que  est équivalente à la résultants
est équivalente à la résultants 
Deuxièmement, convertir 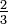 en douzièmes en multipliant le numérateur et le dénominateur par quatre:
en douzièmes en multipliant le numérateur et le dénominateur par quatre:  . Notez que
. Notez que 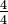 est équivalent à 1, ce qui montre que
est équivalent à 1, ce qui montre que 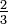 est équivalente à la résultants
est équivalente à la résultants 
Maintenant, on peut voir que:
est équivalent à:
Cette méthode fonctionne toujours, mais parfois il ya un dénominateur plus petit qui peut être utilisé (un dénominateur commun moins). Par exemple, pour ajouter  et
et  le dénominateur 48 peut être utilisé (le produit de 4 à 12), mais le plus petit dénominateur 12 peut également être utilisé, étant le moins commun multiple de 4 et 12.
le dénominateur 48 peut être utilisé (le produit de 4 à 12), mais le plus petit dénominateur 12 peut également être utilisé, étant le moins commun multiple de 4 et 12.
Soustraction
Le processus de soustraction de fractions est, en substance, la même que celle de les ajouter: trouver un dénominateur commun, et de changer chaque fraction d'une fraction équivalente avec le dénominateur commun choisi. La fraction résultante aura que dénominateur et au numérateur sera le résultat de la soustraction des numérateurs des fractions initiales. Par exemple,
Multiplication
Lorsque multipliant ou en divisant, il peut être possible de choisir d'annuler le bas transversalement multiples qui partagent un facteur commun. Par exemple:
1/ 2 1 X 1/ 7 1 = 1/1 X 1/1. Ce qui suit explique comment remplir cette équation.
La multiplication par un nombre entier
Considérant l'exemple ci-dessus du gâteau, si vous avez un quart du gâteau et vous multipliez le montant par trois, puis vous vous retrouvez avec trois quarts. Nous pouvons écrire cette numériquement comme suit:
Comme autre exemple, supposons que cinq personnes travaillent pendant trois heures sur une journée de sept heures (ie. Pour trois septièmes de la journée de travail). Au total, ils ont travaillé pendant 15 heures (5 x 3 heures chacun), ou 15/7 d'un jour. Depuis 7/7 d'une journée est une journée entière et 14/7 est de deux jours, puis au total, ils ont travaillé pendant deux jours et septième d'une journée. Numériquement:
La multiplication par fractions
Considérant l'exemple ci-dessus du gâteau, si vous avez un quart du gâteau et vous multipliez le montant par un troisième, puis vous vous retrouvez avec un douzième du gâteau. En d'autres termes, un tiers du quart (ou un tiers fois quart) est douzième. Pourquoi? Parce que nous répartissons chaque trimestre en trois morceaux, et quatre quarts fois trois rend 12 parties (ou douzièmes). Nous pouvons écrire cette numériquement comme suit:
Comme autre exemple, supposons que cinq personnes font un travail de montant égal qui totalise trois heures sur une journée de sept heures. Chaque personne aura fait un cinquième du travail, de sorte qu'ils ont travaillé pour un cinquième des trois septièmes d'un jour. Numériquement:
Règle générale
Vous avez peut-être remarqué que lorsque nous multiplions fractions, nous multiplions les deux numérateurs (les numéros en haut) pour que le nouveau numérateur, et multiplient les deux dénominateurs (les numéros en bas) pour rendre le nouveau dénominateur. Par exemple:
Multiplication par nombres fractionnaires
Lors de la multiplication de nombres fractionnaires, il est préférable de convertir toute la partie du nombre mixte en une fraction. Par exemple:
Autrement dit,  est le même que
est le même que  , Faisant 11/4 au total (parce que deux gâteaux, chacun divisé en quarts rend 8/4 total) et 33/4 quels
, Faisant 11/4 au total (parce que deux gâteaux, chacun divisé en quarts rend 8/4 total) et 33/4 quels 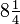 , Depuis huit gâteaux, chacun en quarts, est 32/4 au total.
, Depuis huit gâteaux, chacun en quarts, est 32/4 au total.
Division
Pour diviser par une fraction, il suffit de multiplier par l'inverse de la fraction.
Pour comprendre comment cela fonctionne, considérez ce qui suit:
- Question, ne
- Compte tenu / Accepté
- I. Ne importe quel nombre divisé par lui-même est une (par exemple
 )
) - JE JE. Lorsqu'un nombre est multiplié par une elle ne change pas (par exemple,
 )
) - III. Si deux fractions ont des dénominateurs communs, les numérateurs peuvent être divisée pour trouver le quotient (par exemple
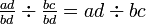 )
)
- I. Ne importe quel nombre divisé par lui-même est une (par exemple
- Preuve
- 1.
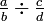 , Problème
, Problème - 2.
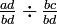 , Multiplié par la première fraction
, Multiplié par la première fraction 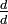 et la seconde fraction par
et la seconde fraction par  , Qui est le même que la multiplication par un, et comme acceptée ci-dessus (I & II) ne change pas la valeur de la fraction
, Qui est le même que la multiplication par un, et comme acceptée ci-dessus (I & II) ne change pas la valeur de la fraction
- 1.
- Remarque: Ces valeurs d'un ont été choisis de sorte que les fractions auraient un dénominateur commun; bd est le dénominateur commun.
- 3.
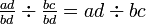 , De ce qui était donné dans (III)
, De ce qui était donné dans (III) - 4.
 , La notation Changé
, La notation Changé - 5.
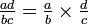 , Peut être vu
, Peut être vu - 6.
 Solution
Solution
- 3.
Il ya environ 4000 ans Egyptiens divisés en fractions en utilisant des méthodes légèrement différentes, l'utilisation de multiples communes avec moins fractions de parts.
Conversion de nombres décimaux périodiques aux fractions
Les nombres décimaux, alors que sans doute plus utile de travailler avec lors de calculs, ne ont pas le même genre de précision que les fractions régulières (comme elles sont expliquées dans cet article) ont. Parfois, un nombre infini de décimales est nécessaire pour transmettre le même genre de précision. Ainsi, il est souvent utile pour convertir des nombres décimaux en fractions de répétition.
Pour modèles les plus répétitifs, une simple division du motif par le même nombre de neufs que les numéros qu'elle a suffira. Par exemple (le motif est souligné en gras):
- 0. 5 ... 55 = 5/9
- 0. 264 264 264 = 264/999 ...
- 0. 6291 62916291 ... = 6291/9999
En cas zéros précèdent le modèle, quatre épingles sont suffixés par le même nombre de zéros:
- 0,0 5 ... 55 = 5/90
- 0,000 392 392 392 ... = 392/999000
- 0,00 12 1212 ... = 12/9900
Dans le cas d'un ensemble non-répétition de décimales précéder le modèle (comme 0,1523 987 987 987 ...), nous devons assimiler comme la somme des parties non-répétition et répétition:
- 0,1523 + ,0000987987987 ...
Ensuite, convertissez ces deux fractions. Étant donné que la première partie ne est pas répéter, il ne est pas converti selon le schéma donné ci-dessus:
- 1523/10000 987/9990000 +
Nous ajoutons ces fractions en exprimant à la fois avec un diviseur commun ...
- 1521477/9990000 + 987/9990000
Et les ajouter.
- 1522464/9990000
Enfin, nous simplifions il:
- 31718/208125
Cas particuliers
Une fraction d'unité est une fraction avec un numérateur vulgaire de 1, par exemple, 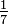 .
.
Une Fraction égyptienne est la somme des fractions de parts distinctes, par exemple  .
.
Un fraction dyadique est une fraction vulgaire dans lequel le dénominateur est un puissance de deux, par exemple,  .
.
Une expression qui a la forme d'une fraction, mais représente en fait une division par ou dans un nombre irrationnel est parfois appelé «fraction irrationnelle». Un exemple courant est 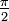 , La mesure radian d'un angle droit.
, La mesure radian d'un angle droit.
Les nombres rationnels sont les champ de quotient de nombre entiers. Fonctions rationnelles sont fonctions évaluées sous la forme d'une fraction, où le numérateur et le dénominateur sont des polynômes. Ces expressions rationnelles sont le domaine des quotient polynômes (sur certaines domaine intégrante).
Un fraction continue est une expression telle que  Où les a i sont des nombres entiers. Ce ne est pas un élément d'un champ de quotient.
Où les a i sont des nombres entiers. Ce ne est pas un élément d'un champ de quotient.
Le terme fraction partielle est utilisée en algèbre, lors de la décomposition des expressions rationnelles (une fraction avec une expression algébrique dans le dénominateur). Le but est d'écrire l'expression rationnelle comme la somme des autres expressions rationnelles avec des dénominateurs de moindre degré. Par exemple, l'expression rationnelle  peut être réécrite comme la somme de deux fractions:
peut être réécrite comme la somme de deux fractions: 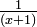 et
et  .
.
Outils pédagogiques
En écoles primaires, des fractions ont été démontrées par Réglettes Cuisenaire.
Les parents d'enfants fractions d'apprentissage doivent également être conscients que l'arithmétique est souvent enseigné très différemment avec mathématiques de réforme. De nombreux textes ne donnent pas instruction de méthodes normalisées qui peuvent utiliser le plus petit dénominateur commun, de comparer ou ajouter des fractions. Certains introduire des concepts nouvellement développés comme "les bandes de fractions» et fractions de référence (1/2, 1/4, 3/4 et 1/10) qui ne sont pas familiers aux parents ou aux mathématiciens. Certains craignent que de telles méthodes ne seront pas préparer les étudiants pour les mathématiques au collège ou au lycée. Si ce est le cas, les parents peuvent demander leurs écoles pour compléter l'apprentissage de leurs enfants avec des méthodes standard ou passer à des textes qui donnent l'enseignement des méthodes traditionnelles. Fraction arithmétique est normalement enseigné et maîtrisé de la fin de l'élémentaire au secondaire intermédiaire ou junior. Cependant, certains textes tels que les mathématiques connectés ne discutent pas de division de fractions du tout, même à la 8e année en CMP
Voir aussi les liens externes ci-dessous.
Histoire
La première utilisation connue de fractions décimales est ca. 2800 BC comme ancienne vallée de l'Indus unités de mesure . Le Egyptiens utilisaient fractions égyptienne ca. 1000 av. Les Grecs utilisé fractions de parts et plus tard a continué fractions et les adeptes du philosophe grec Pythagore , ca. 530 BC, a découvert que le racine carrée de deux ne peut être exprimée comme une fraction. En 150 BC Mathématiciens Jain en Inde a écrit le «Sthananga Sutra", qui contient les travaux sur la théorie des nombres, des opérations arithmétiques, les opérations avec les fractions .