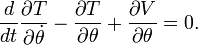Joseph Louis Lagrange

Joseph Louis, comte de Lagrange
Joseph Louis Lagrange
Né	(25/01/1736) Janvier 25, 1736 Turin , Sardaigne
Mort	10 avril 1813 (10/04/1813) (77 ans) Paris , France
Résidence	Sardaigne France Prusse
Nationalité	Sardaigne Français
Les champs	Mathématiques Physique mathématique
Institutions	École Polytechnique
Conseiller de doctorat	Leonhard Euler
Doctorants	Joseph Fourier Giovanni Plana Siméon Poisson
Connu pour	Mécanique analytique La mécanique céleste Analyse mathématique La théorie des nombres
Remarques Remarque il ne avait pas un conseiller de doctorat, mais les autorités académiques de la généalogie lier son patrimoine intellectuel de Leonhard Euler , qui a joué le rôle équivalent.

Joseph-Louis Lagrange, né Giuseppe Lodovico Lagrangia ( 25 janvier 1736 - 10 avril 1813 ) était un Italienne mathématicien et astronome, qui a vécu la plupart de sa vie en France , faisant une contribution exceptionnelle à tous les domaines de l'analyse , à la théorie des nombres , et de classique et la mécanique céleste. Sur la recommandation de Euler et D'Alembert, en 1766 Lagrange Euler réussi en tant que directeur de mathématiques à la Prussienne Académie des sciences de Berlin , où il est resté pendant plus de vingt ans, la production d'un grand nombre de travaux et de gagner plusieurs prix de la Académie française des sciences. Le traité de Lagrange sur mécanique analytique (Mécanique Analytique, 4. ed, 2 vol Paris:.. Gauthier-Villars et fils, de 1888 à 1889), écrit à Berlin et d'abord publié en 1788, a offert le traitement le plus complet de la mécanique classique depuis Newton et formé une base pour le développement de la physique mathématique au XIXe siècle.

Né Giuseppe Lodovico Lagrangia à Turin de parents italiens, Lagrange avait des ancêtres français du côté de son père. En 1787, il est devenu membre de l'Académie française, et il est resté en France jusqu'à la fin de sa vie. Par conséquent, Lagrange est encore considéré comme un Français et un Italien scientifique. Lagrange a survécu à la Révolution française et est devenu le premier professeur d'analyse au École Polytechnique lors de son ouverture en 1794. Napoléon nommé Lagrange à la Légion d'honneur et fait de lui un Le comte de l'Empire en 1808. Il est enterré dans le Panthéon.

Contribution scientifique

Lagrange a été l'un des créateurs du calcul des variations , dériver le Euler-Lagrange équations pour extrema de fonctionnelles. Il a également étendu la méthode à prendre en compte les contraintes possibles, en arrivant à la méthode de Des multiplicateurs de Lagrange. Lagrange a inventé la méthode de résolution des équations différentielles appelées variation de paramètres, appliqué calcul différentiel à la théorie des probabilités et a atteint le travail notable sur la solution de équations. Il a prouvé que chaque nombre naturel est une somme de quatre carrés. Son traité Theorie des fonctions Analytiques mis certains des fondements de la théorie des groupes , anticipant Galois. Dans le calcul , Lagrange a développé une nouvelle approche interpolation et série de Taylor . Il a étudié la problème des trois corps de la Terre, le Soleil et la Lune ( 1764 ) et le mouvement des satellites de Jupiter ( 1766 ), et 1772 a trouvé les solutions spéciale-cas à ce problème qui sont maintenant connus comme Points de Lagrange. Mais surtout il a impressionné sur la mécanique, avoir transformé la mécanique newtonienne dans une branche de l'analyse, Équations de Lagrange comme on dit aujourd'hui, et exposées les «principes» dits mécaniques simples que les résultats du calcul des variations.

Biographie

Les premières années

Lagrange est né, d'origine française et italienne (un grand grand-père paternel était un officier de l'armée française qui a ensuite déménagé à Turin), Giuseppe Lodovico Lagrangia dans Turin . Son père, qui avait la charge de la Royaume de caisse militaire de la Sardaigne, était de bonne position sociale et riche, mais avant que son fils a grandi, il avait perdu la plupart de ses biens dans des spéculations, et le jeune Lagrange a dû compter sur ses propres capacités pour sa position. Il a étudié à l'université de Turin, mais il ne était pas jusqu'à ce qu'il était dix-sept ans qu'il a montré tout goût pour les mathématiques - son intérêt pour le sujet étant d'abord excité par un document par Edmund Halley dont il est tombé par accident. Seul et sans aide, il se jeta dans les études mathématiques; à la fin de incessant labeur de un an, il était déjà un mathématicien accompli, et a été fait d'un professeur de l'école d'artillerie.

Variational calcul

Lagrange est l'un des fondateurs de calcul des variations . À partir de 1754, il a travaillé sur le problème de la tautochrone, en découvrant un procédé de maximisation fonctionnelles et de minimiser d'une manière similaire à la recherche des extremums des fonctions. Lagrange a écrit plusieurs lettres à Leonhard Euler entre 1754 et 1756 décrivant ses résultats. Il a souligné son "δ-algorithme", conduisant à la Euler-Lagrange équations de calcul des variations et de simplifier considérablement analyse antérieure d'Euler. Lagrange également appliqué ses idées aux problèmes de la mécanique classique, la généralisation des résultats d'Euler et Maupertuis.

Euler été très impressionné par les résultats de Lagrange. Il a parfois été déclaré que "avec courtoisie caractéristique qu'il retenu un document qu'il avait déjà écrit, qui couvrait une partie du même terrain, afin que le jeune Italien pourrait avoir le temps de terminer son travail, et de revendiquer l'invention incontesté du nouveau calcul "Cependant, ce point de vue chevaleresque est venu à être contestée. Lagrange a publié sa méthode dans deux mémoires de la Société de Turin en 1762 et 1773.

Miscellanées Taurinensia

En 1758 , avec l'aide de ses élèves, Lagrange créé une société, qui a ensuite été incorporé comme Turin Académie des sciences, et la plupart de ses premiers écrits se trouvent dans les cinq volumes de ses opérations, généralement connu sous le nom Miscellanea Taurinensia. Beaucoup de ces documents sont élaborés. Le premier volume contient un article sur la théorie de la propagation du son; en cela, il indique une erreur commise par Newton , obtient le grand équation différentielle pour le mouvement, et l'intègre pour un mouvement en ligne droite. Ce volume contient également la solution complète du problème d'une corde vibrante transversalement; dans cet article, il souligne un manque de généralité dans les solutions précédemment donnés par Brook Taylor, D'Alembert, Euler et, et arrive à la conclusion que la forme de la courbe à tout moment t est donnée par l'équation . L'article conclut par une discussion magistrale d'échos, beats et des sons composés. Autres articles dans ce volume sont sur récurrent série, probabilités et le calcul des variations .

Le second volume contient un long document reprenant les résultats de plusieurs articles dans le premier volume sur la théorie et la notation du calcul des variations; et il illustre son utilisation par déduire la principe de moindre action, et par des solutions de divers problèmes dans la dynamique.

Le troisième volume comprend la solution de plusieurs problèmes dynamiques au moyen du calcul des variations; quelques papiers sur le calcul intégral ; une solution de Fermat problème s 'mentionné ci-dessus, pour trouver un nombre x qui fera (x ² n + 1) un carré où n est un entier donné qui ne est pas un carré; et les équations différentielles générales de Proposition de trois corps en mouvement sous leurs attractions mutuelles.

Le prochain travail qu'il produit était en 1764 sur le libration de la Lune , et une explication des raisons pour lesquelles le même visage a toujours été tourné vers la terre, un problème dont il traite à l'aide de travail virtuel. Sa solution est particulièrement intéressante comme contenant le germe de l'idée d'équations généralisées de mouvement, équations qui il a d'abord formellement prouvé en 1780 .

Berlin Académie

Déjà en 1756 Euler, avec le soutien de Maupertuis, fait une tentative de mettre Lagrange à l'Académie de Berlin. Plus tard, D'Alembert intervenu au nom de Lagrange avec Frédéric de Prusse et écrivit à Lagrange lui demandant de quitter Turin pour une position beaucoup plus prestigieuse à Berlin. Lagrange a refusé les deux offres, répondant en 1765 que

Il me semble que Berlin ne serait pas du tout adapté pour moi tout M.Euler est là.

En 1766 Euler a quitté Berlin pour Saint-Pétersbourg , et Frédéric de Lagrange écrit exprimant le souhait de «le plus grand roi en Europe" d'avoir "le plus grand mathématicien en Europe« résident à sa cour. Lagrange a finalement été convaincu et il a passé les vingt prochaines années Prusse, où il a produit non seulement la longue série d'articles publiés dans les opérations de Berlin et Turin, mais son œuvre monumentale, l'analytique Mécanique. Sa résidence à Berlin a commencé par une erreur malheureuse. Trouver la plupart de ses collègues mariés, et assurée par leurs femmes que ce était le seul moyen d'être heureux, il se est marié; sa femme mourut bientôt, mais le syndicat ne était pas heureuse.

Lagrange était un favori du roi, qui a utilisé fréquemment au discours lui sur les avantages de la parfaite régularité de la vie. La leçon est rentré chez lui, et dès lors Lagrange étudia son esprit et le corps comme se ils étaient des machines, et a constaté par expérience, le montant exact de travail qu'il était capable de faire, sans tomber en panne. Chaque nuit, il se est fixé une tâche définie pour le lendemain, et sur l'achèvement de ne importe quelle branche d'un sujet, il a écrit une brève analyse pour voir quels sont les points dans les manifestations ou dans l'objet était susceptible d'amélioration. Il a toujours pensé le sujet de ses papiers avant de commencer à les composer, et généralement les écrivit emblée sans une seule rature ni surcharge.

France

En 1786 , Frédéric est mort, et Lagrange, qui avait trouvé le climat de Berlin essayer, a accepté avec plaisir l'offre de Louis XVI à migrer vers Paris. Il a reçu des invitations similaires de l'Espagne et Naples. En France, il a été reçu avec toutes les marques de distinction et spéciaux appartements du Louvre ont été préparé pour sa réception, et il est devenu un membre de la Académie française des sciences, qui devint plus tard une partie de la Institut national. Au début de son séjour à Paris, il fut pris d'une attaque de la mélancolie, et même la copie imprimée de son Mécanique sur lequel il avait travaillé pendant un quart de siècle resta plus de deux ans non ouverts sur son bureau. Curiosité quant aux résultats de la Révolution française l'ai agité de sa léthargie, une curiosité qui est vite transformée en alarme la révolution développé.

Il était environ le même temps, 1792 , que la tristesse inexplicable de sa vie et sa timidité déplacée de la compassion d'une jeune fille qui a insisté pour se marier avec lui, et se est avéré une femme dévouée à qui il se est vivement attaché. Bien que le décret du Octobre 1793 qui a ordonné à tous les étrangers de quitter la France qui lui est expressément dispensé par son nom, il se apprêtait à se échapper quand on lui a offert la présidence de la commission pour la réforme des poids et mesures. Le choix des unités finalement retenus était en grande partie grâce à lui, et il a été principalement dû à son influence que la décimale a été accepté par la commission de 1799 . En 1795, Lagrange fut l'un des membres fondateurs de la Bureau des Longitudes.

Bien que Lagrange avait déterminé à se échapper de la France alors qu'il était encore temps, il n'a jamais été en danger; et les différents gouvernements révolutionnaires (et à un moment plus tard, Napoléon ) lui chargés d'honneurs et distinctions. Un témoignage frappant au respect dans laquelle il a été détenu a été montré dans 1796 lorsque le commissaire français en Italie a été condamnée à assister en pleine État sur le père de Lagrange, et tendre les félicitations de la république sur les réalisations de son fils, qui «avait fait honneur à l'humanité tout entière par son génie, et que ce était la gloire spéciale de Piémont avoir produit. " On peut ajouter que Napoléon, quand il atteint le pouvoir, chaleureusement encouragé études scientifiques en France, et a été un bienfaiteur libérale d'entre eux.

École normale

En 1795 , Lagrange a été nommé à une chaire mathématique au nouvellement créé École normale, qui ne bénéficiait que d'une brève existence de quatre mois. Ses conférences étaient ici tout à fait élémentaire, et contiennent rien de toute importance particulière, mais ils ont été publiés parce que les professeurs devaient "se engager à les représentants du peuple et de l'autre ni à lire ni à répéter de mémoire,» et les discours ont été condamnés à être prises en sténographie afin de permettre aux députés de voir comment les professeurs se acquittèrent.

École Polytechnique

Lagrange a été nommé professeur de la École Polytechnique en 1794; et ses conférences, il sont décrits par les mathématiciens qui ont eu la chance de pouvoir y assister, comme presque parfaite tant dans la forme et la matière. En commençant par les éléments Mer, il a mené ses auditeurs jusqu'à, presque à leur insu, ils se étaient étendant les limites de l'objet: avant tout il a impressionné sur ses élèves l'avantage de toujours utiliser des méthodes générales exprimées dans une notation symétrique.

D'autre part, Fourier, qui a assisté à ses conférences en 1795, a écrit:

Sa voix est très faible, au moins en ce qu'il ne devienne pas chauffée; il a un accent italien très prononcé et prononce les s comme z ... Les étudiants, dont la majorité sont incapables de l'apprécier, lui donner peu les bienvenus, mais les professeurs de faire amende honorable pour elle.

Ans de retard

La tombe de Lagrange dans la crypte de la Panthéon.

En 1810 , Lagrange a entamé une révision approfondie de la Mécanique analytique, mais il a pu terminer seulement environ les deux tiers de celui-ci avant sa mort en 1813. Il a été enterré la même année dans le Panthéon à Paris. Le texte français sur sa tombe il lit:

Joseph Louis Lagrange. Le sénateur. Comte de l'Empire. Grand Officier de la Légion d'honneur. Grand-Croix de l'Ordre impérial de la Réunion. Membre de l'Institut et le Bureau des longitudes. Né à Turin le 25 Janvier 1736. Décédé à Paris le 10 Avril 1813.

Travail à Berlin

Lagrange était scientifiquement très actif pendant vingt années qu'il a passées à Berlin. Non seulement at-il produire sa splendide analytique Mécanique, mais il a contribué entre un et deux cents documents à l'Académie de Turin, l'Académie de Berlin, et de l'Académie française. Certains d'entre eux sont vraiment traités, et tous sans exception sont d'un ordre élevé de l'excellence. Sauf pour un court laps de temps quand il était malade, il a produit en moyenne environ un papier d'un mois. Parmi ceux-ci, noter ce qui suit comme parmi les plus importants.

Tout d'abord, ses contributions aux quatrième et cinquième volumes, 1766 - 1,773 , de la Miscellanea Taurinensia; dont le plus important était celui de 1771 , dans lequel il a discuté de la façon dont de nombreux astronomiques observations devraient être combinées de manière à donner le résultat le plus probable. Et plus tard, ses contributions aux deux premiers volumes, 1784 - 1785 , des opérations de l'Académie de Turin; à la première dont il a présenté un document sur la pression exercée par les fluides en mouvement, et à la seconde un article sur l'intégration par série infinie, et du genre de problèmes pour lesquels il est adapté.

La plupart des documents envoyés à Paris étaient sur les questions astronomiques, et parmi ceux-ci on doit mentionner en particulier son article sur la Système jovien en 1766, son essai sur le problème des trois corps dans 1772 , son travail sur le équation séculaire de la Lune dans 1773 , et son traité sur les perturbations cométaires en 1778. Ceux-ci ont tous été écrits sur des sujets proposés par le Académie française, et dans chaque cas le prix lui a été décerné.

Équations de Lagrange

Entre 1772 et 1788, Lagrange reformulé la mécanique newtonienne classique / de simplifier les formules et la facilité des calculs. Ces mécaniciens sont appelés Équations de Lagrange.

Algèbre

Le plus grand nombre de ses papiers au cours de cette époque étaient, cependant, contribué à la Académie des sciences de Prusse. Plusieurs d'entre eux traitent de questions dans l'algèbre .

• Sa discussion de représentations de nombres entiers par formes quadratiques (1769) et par des formes algébriques plus générales (1770).
• Son tube sur la Théorie de l'élimination, 1770.
• Le théorème de Lagrange que l'ordre d'un sous-groupe H d'un groupe G doit diviser l'ordre de G.
• Ses papiers de 1770 et 1771 sur le processus général pour résoudre un équation algébrique de tout degré via les résolvantes de Lagrange. Cette méthode ne donne pas une formule générale pour les solutions d'une équation de degré cinq ans et plus, car il l'équation auxiliaire a participé degré plus élevé que celui d'origine. L'importance de cette méthode est qu'il présente les formules déjà connus pour résoudre les équations de deuxième, troisième, et quatrième degrés comme maniferstations d'un principe unique. La solution complète d'une équation binôme de tout degré est également traitée dans ces documents.
• En 1773, Lagrange considéré comme un déterminant fonctionnel d'ordre 3, un cas particulier d'un Jacobienne. Il se est avéré également l'expression de la volumique d'un tétraèdre avec l'un des sommets à l'origine comme le sixième de la valeur absolue du déterminant formée par les coordonnées des trois autres sommets.

Théorie des nombres

Plusieurs de ses premiers articles traitent aussi de questions de la théorie des nombres.

• Lagrange (1766-1769) fut le premier à prouver que L'équation de Pell 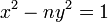a une solution non triviale dans les nombres entiers pour tout non-carré nombre naturel n.
• Il a prouvé le théorème, a déclaré par Bachet sans justification, que tout entier positif est la somme de quatre carrés, 1770.
• Il a prouvé Théorème de Wilson que si n est un nombre premier, alors (n - 1)! + 1 est toujours un multiple de n, 1771.
• Ses papiers de 1773, 1775 et 1777 ont fait des démonstrations de plusieurs résultats énoncés par Fermat, et non prouvé précédemment.
• Il a donné une méthode pour déterminer les facteurs de nombres de la forme

Autres travaux mathématiques

Il ya aussi de nombreux articles sur divers points de la géométrie analytique . Dans deux d'entre eux, écrit et non plus tard, en 1792 et 1793 , il a réduit le équations des quadriques (ou) à leur conicoids formes canoniques.

Pendant les années de 1772 à 1785 , il a contribué une longue série de documents qui ont créé la science des équations aux dérivées partielles . Une grande partie de ces résultats ont été recueillies dans la deuxième édition du calcul intégral d'Euler qui a été publié en 1794 .

Il a apporté des contributions à la théorie des fractions continues.

Astronomie

Enfin, il existe de nombreux articles sur les problèmes de l'astronomie . Parmi ceux-ci le plus important sont les suivants:

• Tenter de résoudre le problème des trois corps résultant dans la découverte de Points de Lagrange, 1772
• Sur l'attraction des ellipsoïdes, 1773: ce est fondée sur Le travail de Maclaurin.
• Sur l'équation séculaire de la Lune, 1773; également notable pour la première introduction de l'idée du potentiel. Le potentiel d'un corps en un point quelconque est la somme de la masse de chaque élément du corps lorsqu'elle est divisée par la distance du point. Lagrange a montré que si le potentiel d'un corps à un point extérieur était connue, l'attraction dans toutes les directions à la fois pourrait être trouvé. La théorie du potentiel a été élaborée dans un document envoyé à Berlin en 1777.
• Sur le mouvement des nœuds d'une planète de orbite, 1774.
• Sur la stabilité des orbites planétaires, 1776.
• Deux papiers dans lesquels la méthode de détermination de l'orbite d'une comète à partir de trois observations est complètement élaboré, 1778 et 1783: ce est en effet pas prouvé pratiquement disponibles, mais son système de calcul des perturbations au moyen de quadratures mécaniques a formé la base de la plupart des recherches ultérieures sur le sujet.
• Sa détermination des variations séculaires et périodiques de la éléments des planètes, 1781-1784: les limites supérieures attribuées à celles-ci acceptent en étroite collaboration avec ceux obtenus plus tard par Le Verrier et Lagrange ont procédé dans la mesure où la connaissance possédait alors des masses des planètes autorisées.
• Trois documents sur la méthode d'interpolation, 1783, 1792 et 1793: la part des différences finies traitant celui-ci est maintenant dans le même stade que celui dans lequel Lagrange laissé.

Mécanique analytique

Au-delà de ces divers documents, il composa son grand traité, l'analytique Mécanique. En cela, il fait la loi du travail virtuel, et à partir de ce principe fondamental une, à l'aide du calcul des variations, en déduit l'ensemble de la mécanique, à la fois des solides et des fluides.

L'objet de ce livre est de montrer que le sujet est implicitement inclus dans un seul principe, et à donner formules générales à partir de laquelle un résultat particulier peut être obtenue. La méthode de coordonnées généralisées par lequel il a obtenu ce résultat est peut-être le résultat le plus brillant de son analyse. Au lieu de suivre le mouvement de chaque partie d'un système matériel, que D'Alembert et Euler avaient fait, il a montré que, si nous déterminons sa configuration par un nombre suffisant de variables dont le nombre est le même que celui des degrés de liberté possédé par le système, alors les énergies cinétiques et potentielles du système peuvent être exprimés en termes de ces variables et les équations différentielles du mouvement de là, déduit par simple différenciation. Par exemple, dans la dynamique d'un système rigide, il remplace l'examen du problème particulier par l'équation générale, qui est maintenant généralement écrite sous la forme

T pour l'énergie cinétique et V pour l'énergie potentielle. Parmi d'autres théorèmes mineures ici donnés, il peut parler de la proposition que l'énergie cinétique communiquée par les impulsions données à un système matériel sous contraintes données est un maximum, et principe de moindre action. Toutes les analyses est si élégant que Sir William Rowan Hamilton dit que le travail ne peut être décrit comme un poème scientifique. Il peut être intéressant de noter que Lagrange a fait remarquer que la mécanique était vraiment une branche des mathématiques pures analogues à une géométrie à quatre dimensions, à savoir, le temps et les trois coordonnées du point dans l'espace; et il est dit qu'il se vantait que du début à la fin du travail, il ne était pas un seul diagramme. Au début, aucune imprimante ne pourrait être trouvée qui publie le livre; mais Legendre enfin persuadé une firme de Paris à l'entreprendre, et il a été publié sous sa supervision en 1788.

Une contribution importante à la mécanique des fluides est le concept de "flux potentiel», souvent associé, à tort, avec la notion de, fluide parfait idéal. Le développement initial de Joseph-Louis Lagrange (1781) présente le potentiel de vitesse pour le fluide se écoule réels, à condition que la résultante des forces dérive d'un potentiel. Dans le même article, Lagrange a également présenté le concept de fonction de courant et l'équation de la célérité d'une petite perturbation dans l'eau peu profonde. La contribution de Lagrange en 1781 était exceptionnel et était vraiment en avance sur son temps.

Travail en France

Le calcul différentiel et calcul des variations

Les conférences de Lagrange sur le calcul différentiel à l'École Polytechnique forment la base de son traité Théorie des Fonctions Analytiques, qui a été publié en 1797. Cet ouvrage est le prolongement d'une idée contenue dans un document qu'il avait envoyé aux journaux de Berlin en 1772, et son objet est de substituer pour le calcul différentiel un groupe de théorèmes basés sur le développement de fonctions algébriques en série. Une méthode un peu similaire avait été utilisé précédemment par John Landen dans l'analyse résiduelle, publié à Londres en 1758. Lagrange croyait qu'il pourrait ainsi se débarrasser de ces difficultés, liées à l'utilisation de l'infiniment grand et infiniment petites quantités, à laquelle les philosophes opposé dans le traitement habituel du calcul différentiel. Le livre est divisé en trois parties: de ceux-ci, la première traite de la théorie générale des fonctions, et donne une preuve algébrique du théorème de Taylor , dont la validité est cependant ouverte à la question; le second porte sur les applications à la géométrie; et le troisième avec des applications à la mécanique. Un autre traité sur les mêmes lignes était ses Leçons sur le calcul des fonctions, publié en 1804 , avec la deuxième édition en 1806. Ce est dans ce livre que Lagrange a formulé sa célèbre méthode de Multiplicateurs de Lagrange, dans le contexte des problèmes de calcul des variations des contraintes intégrales. Ces ouvrages consacrés au calcul différentiel et calcul des variations peuvent être considérés comme le point de départ pour les recherches de Cauchy, Jacobi, et Weierstrass.

Infinitesimals

Plus tard Lagrange revient à l'utilisation de infinitésimales dans les préférences de fonder le calcul différentiel sur l'étude des formes algébriques; et dans la préface à la deuxième édition de la Mécanique, qui a été publié en 1811 , il justifie l'emploi des infinitésimaux, et conclut en disant que:

Lorsque nous avons saisi l'esprit de la méthode infinitésimale, et nous avons vérifié l'exactitude de ses résultats soit par la méthode géométrique des ratios premiers et ultimes, ou par la méthode d'analyse des fonctions dérivées, on peut employer des quantités infiniment petites comme sûr et précieux les moyens de raccourcir et de simplifier nos preuves.

Fractions continues

Sa résolution des équations Numériques, publié en 1798 , était aussi le fruit de ses conférences à l'École polytechnique. Là, il donne la méthode d'approximation aux véritables racines d'une équation au moyen de fractions continues, et énonce plusieurs autres théorèmes. Dans une note à la fin il montre comment Le petit théorème de Fermat qui

un ^{p -1-1} ≡ 0 (mod p)

où p est un nombre premier et un est premier à p, peuvent être appliqués pour donner une solution complète de toute équation algébrique binomiale. Il explique également comment ici l'équation dont les racines sont les carrés des différences des racines de l'équation d'origine peuvent être utilisés de manière à donner des informations considérables quant à la position et la nature de ces racines.

La théorie de la mouvements planétaires avaient fait l'objet d'une partie de la plus remarquable des journaux de Berlin de Lagrange. En 1806 le sujet a été rouverte par Poisson, qui, dans un document lu devant l'Académie française, ont montré que les formules de Lagrange ont conduit à certaines limites pour la stabilité des orbites. Lagrange, qui était présent, maintenant l'ensemble du sujet discuté à nouveau, et dans une lettre communiquée à l'Académie en 1808 a expliqué comment, par la variation des constantes arbitraires, la revue et les inégalités séculaires de tout système d'organismes qui interagissent mutuellement pu être déterminées.

Prix et distinctions

Euler Lagrange proposé à l'élection à l'Académie de Berlin et il a été élu le 2 Septembre, 1756. Il a été élu Fellow de la Royal Society of Edinburgh en 1790, et un membre de la Royal Society en 1791. En 1808 , Napoléon fait Lagrange Grand Officier de la Légion d'honneur et un Comte de l'Empire. Il a reçu le Grand Croix de la Ordre Impérial de la Réunion en 1813 , une semaine avant sa mort à Paris.

Lagrange a reçu le prix 1764 de la Académie française des sciences pour son mémoire sur la libration de la Lune. En 1766, l'Académie a proposé un problème du mouvement de la satellites de Jupiter, et le prix a été décerné à nouveau Lagrange. Il a également remporté les prix de 1772, 1774 et 1778.

Lagrange est l'un des 72 éminents scientifiques français qui ont été commémorée sur des plaques à la première étape de la Tour Eiffel lors de son ouverture. Rue Lagrange dans le 5ème arrondissement de Paris est nommé d'après lui. À Turin, la rue où la maison de sa naissance est toujours debout est nommé par Lagrange. Cratère lunaire Lagrange porte également son nom.

Apocryphes

• Il était de taille moyenne et un peu formée, avec des yeux bleus et le teint pâle incolore. Il était nerveux et timide, il détestait la controverse, et, pour l'éviter, volontairement permis aux autres de prendre le crédit pour ce qu'il avait fait.

• Il est dit qu'il était capable d'écrire ses papiers complet sans une seule correction nécessaire.