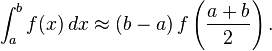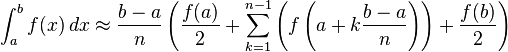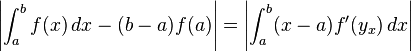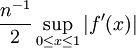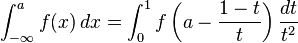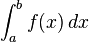L'intégration numérique
Renseignements généraux
Cette sélection Wikipedia est déconnecté disponibles à partir enfants SOS pour la distribution dans le monde en développement. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
En analyse numérique, intégration numérique constitue une large famille d'algorithmes de calcul de la valeur numérique d'une certaine intégrante , et par extension, le terme est parfois utilisé pour décrire la solution numérique des équations différentielles. Cet article se concentre sur le calcul des intégrales définies. La quadrature numérique terme (souvent abrégé en quadrature) est plus ou moins un synonyme pour l'intégration numérique, en particulier telle qu'elle est appliquée à des intégrales unidimensionnelles. L'intégration numérique sur plus d'une dimension est parfois décrit comme cubage, bien que le sens de quadrature est entendu pour l'intégration de plus grande dimension ainsi.
Le problème de base considéré par intégration numérique est de calculer une solution approchée d'une intégrale définie:
Si f (x) est une fonction lisse bien comportés, intégré sur un petit nombre de dimensions et les limites de l'intégration sont limitées, il existe de nombreuses méthodes d'approximation de l'intégrale avec une précision arbitraire.
Raisons de l'intégration numérique
Il existe plusieurs raisons pour effectuer une intégration numérique. Le f intégrand (x) peut être connu seulement à certains points, comme obtenu par échantillonnage . Certains systèmes embarqués et d'autres applications informatiques peuvent avoir besoin d'intégration numérique pour cette raison.
Une formule pour l'intégrale peut être connu, mais il peut être difficile ou impossible de trouver un primitive qui est une fonction élémentaire. Un exemple d'une telle fonction à intégrer est f (x) = exp (- x 2), dont la primitive (la fonction d'erreur, une fois constants) ne peuvent pas être écrites dans forme élémentaire.
Il peut être possible de trouver une primitive symboliquement, mais il peut être plus facile à calculer une approximation numérique que de calculer la primitive. Ce est peut-être le cas si la primitive est donnée comme une série infinie ou d'un produit, ou si son évaluation nécessite une fonction spéciale qui ne est pas disponible.
Méthodes pour intégrales unidimensionnelles
Méthodes d'intégration numérique peut généralement être décrit comme une combinaison des évaluations de l'intégrale pour obtenir une approximation de l'intégrale. L'intégrale est évaluée à un ensemble fini de points appelés points d'intégration et une somme pondérée de ces valeurs est utilisée pour calculer l'intégrale. Les points d'intégration et de poids dépendent de la méthode utilisée et la précision requise de l'approximation.
Une partie importante de l'analyse d'une méthode d'intégration numérique est d'étudier le comportement de l'erreur d'approximation en fonction du nombre d'évaluations de intégrand. Un procédé qui produit une petite erreur pour un petit nombre d'évaluations est généralement considéré comme supérieur. Réduire le nombre d'évaluations de la fonction à intégrer réduit le nombre d'opérations arithmétiques en cause, et donc réduit le total erreur d'arrondi. En outre, chaque évaluation prend du temps, et l'intégrale peut être arbitrairement compliquée.
Un «force brute» type d'intégration numérique peut être fait, si l'intégrale est raisonnablement bien comporté (c.-à- par morceaux continu et de variation bornée), en évaluant l'intégrant avec de très petits incréments.
Quadrature règles de base sur les fonctions d'interpolation
Une large classe de règles en quadrature peut être dérivée par la construction d'interpolation des fonctions qui sont faciles à intégrer. Généralement, ces fonctions d'interpolation sont des polynômes .
La méthode la plus simple de ce type est de laisser la fonction d'interpolation une fonction constante (un polynôme de degré zéro) qui passe par le point ((a + b) / 2, f ((a + b) / 2)). Ce est ce qu'on appelle la règle milieu ou règle rectangle.
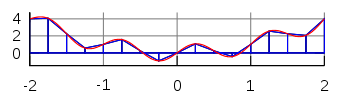
La fonction d'interpolation peut être un fonction affine (un polynôme de degré 1) qui passe par les points (a, f (a)) et (b, f (b)). Ceci est appelé le règle trapézoïdale.
Pour l'une de ces règles, nous pouvons faire une approximation plus précise en brisant l'intervalle [a, b] en un nombre n de sous-intervalles, le calcul d'un rapprochement pour chaque sous-intervalle, puis en ajoutant jusqu'à tous les résultats. Cela se appelle une règle composite, règle étendue, ou la règle itérative. Par exemple, la règle trapézoïdale composite peut être déclaré que
où les sous-intervalles sont de la forme [k h, (k + 1) h], avec h = (b - a) / n et k = 0, 1, 2, ..., n-1.
Interpolation avec polynômes évalués à points également espacés dans [a, b] donne le Formules de Newton-Cotes, dont la règle de rectangle et la règle trapézoïdale sont des exemples. La règle de Simpson, qui est basé sur un polynôme d'ordre 2, est également une formule de Newton-Cotes.
règles de quadrature avec points également espacés ont la propriété très pratique de la nidification. La règle correspondant à chaque intervalle subdivisé comprend tous les points actuels, de sorte que ces valeurs intégrand peut être réutilisé.
Si on laisse les intervalles entre les points d'interpolation pour faire varier, nous trouvons un autre groupe de formules de quadrature, tels que la Formules de quadrature de Gauss. Une règle de quadrature de Gauss est généralement plus précise que la règle de Newton-Cotes qui exige le même nombre d'évaluations de fonctions, si l'intégrale est lisse (ce est à dire, si elle est suffisamment différentiables). Autres méthodes de quadrature avec des intervalles variables comprennent Clenshaw-Curtis quadrature (également appelé quadrature Fejér) méthodes, qui font nid.
Règles de quadrature de Gauss ne nichent pas, mais le connexes Gauss-Kronrod formules de quadrature font.
Algorithmes adaptatifs
Si f (x) n'a pas beaucoup de dérivés en tous points, ou si les dérivés deviennent grand, alors la quadrature de Gauss est souvent insuffisant. Dans ce cas, un algorithme similaire à la suivante sera plus performant:
def calculate_definite_integral_of_f (f, initial_step_size): '' 'Cet algorithme calcule l'intégrale définie d'une fonction 0-1, adaptative, en choisissant petites étapes près des points problématiques. '' 'X = 0,0 h = initial_step_size accumulateur = 0,0 tandis x <1.0: si x + h> 1.0: h = 1,0 - x = quad_this_step si error_too_big_in_quadrature_of_over_range (f, [x, x + h]): h = make_h_smaller (h ) else: accumulateur + = quadrature_of_f_over_range (f, [x, x + h]) x + = h si error_too_small_in_quadrature_of_over_range (f, [x, x + h]): h = make_h_larger (h) # Éviter de perdre du temps sur de minuscules étapes. retour accumulateur
Certains détails de l'algorithme demandent une réflexion sérieuse. Pour de nombreux cas, l'estimation de l'erreur de quadrature sur un intervalle d'une fonction f (x) ne est pas évidente. Une solution populaire est d'utiliser deux règles différentes de quadrature, et d'utiliser leur différence comme une estimation de l'erreur de quadrature. L'autre problème est de décider ce que «trop grande» ou «très faible» signifient. Un critère local pour "trop grand" est que l'erreur de quadrature ne devrait pas être plus grand que t · h où t, un nombre réel, est la tolérance que nous souhaitons mettre à l'erreur globale. Et puis, si h est déjà petit, il peut ne pas être intéressant pour le rendre encore plus petit, même si l'erreur de quadrature est apparemment importante. Un critère global est que la somme des erreurs sur tous les intervalles doit être inférieure à t. Ce type d'analyse d'erreur est généralement appelé "a posteriori" puisque nous calculons l'erreur après avoir calculé le rapprochement.
Heuristiques pour quadrature adaptative sont discutés par Forsythe et al. (Section 5.4).
méthodes d'extrapolation
La précision d'une règle de quadrature du type Newton-Cotes est généralement fonction du nombre de points d'évaluation. Le résultat est généralement plus précise que le nombre de points d'évaluation augmente, ou, de manière équivalente, que la largeur de la taille de pas entre les points diminue. Il est naturel de se demander ce que serait le résultat si la taille de l'étape ont été autorisés à approcher de zéro. Cela peut être répondu en extrapolant le résultat de deux ou plusieurs tailles de pas non nulles, en utilisant méthodes d'accélération de série tels que Extrapolation Richardson. La fonction d'extrapolation peut être un polynôme ou fonction rationnelle. méthodes d'extrapolation sont décrites plus en détail par Stoer et Bulirsch (section 3.4) et sont mises en œuvre dans la plupart des routines de la Bibliothèque QUADPACK.
Conservateur (a priori) estimation de l'erreur
Soit f ont une première dérivée bornée sur [a, b]. Le valeur moyenne théorème pour f, où x <b, donne
pour certains y x dans [a, x] en fonction de x. Si nous intégrons dans x de a à b des deux côtés et prendre les valeurs absolues, nous obtenons
Nous pouvons continuer à rapprocher l'intégrale sur le côté droit en apportant la valeur absolue en l'intégrant et en remplaçant le terme dans f 'par une borne supérieure:
(**)
(Voir supremum) Par conséquent, si on approche l'intégrale ∫ a b f (x) d x par la règle de quadrature (b -. a) f (a) notre erreur ne est plus grand que le côté droit de (**). On peut convertir en une analyse des erreurs de la somme de Riemann (*), ce qui donne une borne supérieure de
pour le terme d'erreur de ce rapprochement particulier. (Notez que ce est précisément l'erreur, nous avons calculé pour l'exemple 
.) Utilisation de plusieurs dérivés, et en ajustant la quadrature, nous pouvons faire une analyse d'erreur similaire utilisant une série de Taylor (en utilisant une somme partielle pour une durée de reste) pour f. Cette analyse d'erreur donne une stricte limite supérieure sur l'erreur, si les dérivés de f sont disponibles.
Cette méthode d'intégration peut être combiné avec arithmétique d'intervalle pour produire des preuves informatiques et calculs vérifiés.
Intégrales sur des intervalles infinis
Intervalles infinis
Une façon de calculer une intégrale sur l'intervalle infini,
est le transformer en une intégrale sur un intervalle fini par l'un de plusieurs changements possibles de variables, par exemple:
L'intégrale sur intervalle fini peut ensuite être évaluée par des méthodes d'intégration ordinaires.
Intervalles d'une demi-infinis
Une intégrale sur un intervalle de demi-infini peut également être transformé en une intégrale sur un intervalle fini par l'un de plusieurs changements possibles de variables, par exemple:
De même,
Intégrales multidimensionnelles
Les règles en quadrature examinés jusqu'ici sont tous conçus pour calculer des intégrales unidimensionnelles. Pour calculer des intégrales dans de multiples dimensions, une approche consiste à expression multiple entier comme répétées intégrales unidimensionnelles en faisant appel à Théorème de Fubini. Cette approche nécessite des évaluations de la fonction à croître de façon exponentielle le nombre de dimensions augmente. Deux procédés sont connus pour résoudre ce que l'on appelle malédiction de la dimension.
Monte Carlo
Méthodes de Monte Carlo et méthodes quasi-Monte Carlo sont faciles à appliquer à des intégrales multidimensionnelles, et peuvent donner une plus grande précision pour le même nombre d'évaluations de la fonction que intégrations répétées en utilisant des méthodes unidimensionnelles.
Une grande classe de méthodes de Monte Carlo utiles sont les soi-disant Chaînes de Markov algorithmes de Monte Carlo, qui incluent le Algorithme de Metropolis-Hastings et Échantillonnage de Gibbs.
Grilles Sparse
Sparse grilles ont été initialement développés par Smolyak pour la quadrature des fonctions de haute dimension. La méthode est toujours basé sur un unidimensionnel règle de quadrature, mais effectue une combinaison plus sophistiquée des résultats univariés.
Connexion avec équations différentielles
Le problème de l'évaluation de l'intégrale
peut être réduite à un problème de valeur initiale pour une équation différentielle ordinaire . Si l'intégrale ci-dessus est désigné par I (b), alors la fonction I satisfait
Les méthodes développées pour les équations différentielles ordinaires, tels que Méthodes de Runge-Kutta, peuvent être appliquées au problème retraitées et ainsi être utilisés pour évaluer l'intégrale. Par exemple, le quatrième ordre méthode de Runge-Kutta norme appliquée à l'équation différentielle donne la règle de Simpson d'en haut.
L'équation différentielle I '(x) = f (x) a une forme particulière: la droite ne contient que la variable dépendante (ici x) et non la variable indépendante (ici I). Cela simplifie la théorie et les algorithmes considérablement. Le problème de l'évaluation des intégrales est donc mieux étudié dans son propre droit.
