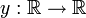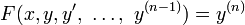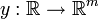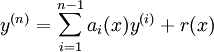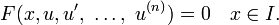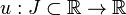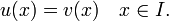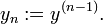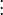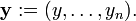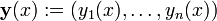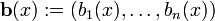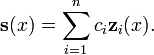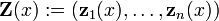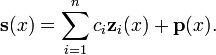Vérifié contenu

Équation différentielle ordinaire

Sujets connexes: Mathématiques

À propos de ce écoles sélection Wikipedia

Ce contenu de Wikipedia a été sélectionné par SOS Enfants d'aptitude dans les écoles à travers le monde. Parrainer un enfant de faire une réelle différence.

En mathématiques , une équation différentielle ordinaire (ou ODE) est une relation qui contient des fonctions d'un seul variable indépendante, et une ou plusieurs de ses dérivés par rapport à cette variable.

Un exemple simple est la deuxième loi de Newton de mouvement, ce qui conduit à l'équation différentielle

m \ frac {d ^ 2 x (t) dt} {^ 2} = F (x (t)), \,

pour le mouvement d'une particule de masse m. En général, la force F dépend de la position de la particule x (t) au temps t, et par conséquent la fonction inconnue x (t) apparaît sur les deux côtés de l'équation différentielle, comme cela est indiqué dans la notation F (x (t )).

Équations différentielles ordinaires sont à distinguer des équations aux dérivées partielles où il ya plusieurs variables indépendantes impliquant dérivées partielles.

Équations différentielles ordinaires se posent dans de nombreux contextes différents, y compris la géométrie, la mécanique, l'astronomie et la modélisation de la population. Beaucoup de mathématiciens célèbres ont étudié équations différentielles et a contribué sur le terrain, y compris Newton , Leibniz , le Famille Bernoulli, Riccati, Clairaut, d'Alembert et Euler .

Beaucoup d'étude a été consacrée à la solution d'équations différentielles ordinaires. Dans le cas où l'équation est linéaire, il peut être résolu par des méthodes analytiques. Malheureusement, la plupart des équations différentielles sont intéressants non linéaire et, à quelques exceptions près, ne peut être résolu exactement. Solutions approximatives sont arrivés à l'aide d'approximations de l'ordinateur (voir équations différentielles ordinaires numériques).

Le une trajectoire de projectile lancé à partir d'un canon suit une courbe déterminée par une équation différentielle ordinaire qui est dérivée de la seconde loi de Newton.

Définitions

Équation différentielle ordinaire

Soit y une fonction inconnue

Y: \ mathbb {R} \ to \ mathbb {R}

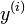en x avec y ^ {(i)} la i ième dérivée de y, puis une fonction

F (x, y, y ', \ \ dots, \ y ^ {(n-1)}) = {y ^ (n)}

est appelé une équation différentielle ordinaire (ODE) d'ordre n. Pour fonctions vectorielles valeur

Y: \ mathbb {R} \ to \ mathbb {R} ^ m

F est appelé un système d'équations différentielles ordinaires de dimension m.

Quand une équation différentielle d'ordre n est de la forme

F \ left (x, y, y ', y' ', \ \ dots, \ y ^ {(n)} \ right) = 0

il est appelé une équation différentielle implicite alors que la forme

F \ left (x, y, y ', y' ', \ \ dots, \ y ^ {(n-1)} \ right) = y ^ {(n)}

est appelé une équation différentielle explicite.

Une équation différentielle non en fonction de x est appelée autonome.

Une équation différentielle est dite linéaire si F peut être écrit comme une combinaison linéaire des dérivés de y

^ {y (n)} = \ sum_ {i = 1} ^ {n-1} a_i (x) ^ {y (i)} + r (x)

avec un i (x) et R (x) des fonctions continues en x. La fonction r (x) est appelé le terme source; si r (x) = 0 alors l'équation différentielle linéaire est dit homogène, sinon il est appelé non homogène ou hétérogène.

Solutions

Compte tenu d'une équation différentielle

F (x, y, y ', \ \ dots, \ ^ {y (n)}) = 0

une fonction

u: Je \ subset \ mathbb {R} \ à \ mathbb {R}

est appelé solution ou courbe intégrale F, si u est n -Times dérivable sur I, F est défini pour tous

(X, u, u ', \ \ dots, \ u ^ {(n)}) \ quad x \ in I

et

F (x, u, u ', \ \ dots, \ u ^ {(n)}) = 0 \ quad x \ in I.

Compte tenu des deux solutions

u: J \ subset \ mathbb {R} \ à \ mathbb {R}

et

v: Je \ subset \ mathbb {R} \ à \ mathbb {R}

u est appelé une extension de v si je ⊂ J et

u (x) = v (x) \ quad x \ in I. \,

Une solution qui n'a pas d'extension se appelle une solution mondiale.

Une solution générale d'une équation d'ordre de n -ième est une solution contenant 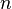n des variables arbitraires, correspondant à n constantes d'intégration. Une solution particulière est dérivé de la solution générale en définissant les constantes à des valeurs particulières, souvent choisi pour remplir SET 'conditions initiales ou aux limites ». Un solution unique est une solution qui ne peut être dérivé de la solution générale.

Exemples

Réduction à un premier système de commande

Toute équation différentielle d'ordre n peut être écrit comme un système d'équations différentielles du premier ordre n. Compte tenu d'une équation différentielle ordinaire explicite d'ordre n et une dimension,

F \ left (x, y, y ', y' ', \ \ dots, \ y ^ {(n-1)} \ right) = y ^ {(n)}

nous définissons une nouvelle famille de fonctions inconnues

y_n: = y ^ {(n-1)} \.!

Nous pouvons alors réécrire l'équation différentielle d'origine comme un système d'équations différentielles à l'ordre 1 et la dimension n.

y_1 ^ '= Y_2
\ vdots
y_n ^ '= F (y_n, \ dots, y_1, x).

qui peut être écrite de façon concise dans la notation de vecteur

\ Mathbf {y} ^ '= \ mathbf {F} (\ mathbf {y}, x)

avec

\ Mathbf {y}: = (y, \ ldots, y_n).

Linéaires des équations différentielles ordinaires

Une classe particulière bien compris des équations différentielles sont des équations différentielles linéaires. Nous pouvons toujours réduire une équation explicite différentiel linéaire de ne importe quel ordre à un système d'équations différentielles d'ordre 1

y_i '(x) = \ sum_ {j = 1} ^ n a_ {i, j} (x) + y_j b_i (x) \, \ mathrm {,} \ quad i = 1, \ ldots, n

que nous pouvons écrire de manière concise en utilisant la notation de vecteur

\ Mathbf {y} ^ '(x) = \ mathbf {A} (x) \ mathbf {y} (x) + \ mathbf {b} (x)

avec

\ Mathbf {y} (x): = (y_1 (x), \ ldots, y_n (x))
\ Mathbf {b} (x): = (b_1 (x), \ ldots, b_n (x))
\ Mathbf {A} (x): = (a_ {i, j} (x)) \, \ mathrm {,} \ quad i, j = 1, \ ldots, n.

Équations homogènes

L'ensemble des solutions pour un système d'équations différentielles linéaires homogènes d'ordre 1 et la dimension n

\ Mathbf {y} ^ '(x) = \ mathbf {A} (x) \ mathbf {y} (x)

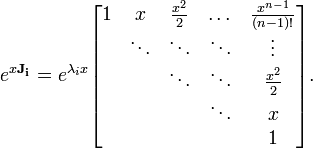
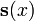forme un n de dimension espace vectoriel . Compte tenu d'une base de cet espace vectoriel \ Mathbf {z} _1 (x), \ ldots, \ mathbf {z} _n (x) , Qui est appelé un système fondamental, toutes les solutions \ Mathbf {s} (x) peut se écrire

\ Mathbf {s} (x) = \ sum_ {i = 1} ^ {n} c_i \ mathbf {z} _i (x).

La matrice n × n

\ Mathbf {Z} (x): = (\ mathbf {z} _1 (x), \ ldots, \ mathbf {z} _n (x))

est appelée matrice fondamentale. En général, il ne existe aucune méthode pour construire explicitement un système fondamental, mais si une solution est connue réduction d'Alembert peut être utilisé pour réduire la dimension de l'équation différentielle par un.

Équations non homogènes

L'ensemble des solutions pour un système d'équations différentielles linéaires homogènes d'ordre 1 et la dimension n

\ Mathbf {y} ^ '(x) = \ mathbf {A} (x) \ mathbf {y} (x) + \ mathbf {b} (x)

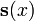peut être construite en trouvant le système fondamental \ Mathbf {z} _1 (x), \ ldots, \ mathbf {z} _n (x) à l'équation homogène correspondante et une solution particulière \ Mathbf {p} (x) à l'équation inhomogène. Chaque solution \ Mathbf {s} (x) l'équation inhomogène peut alors être écrite comme

\ Mathbf {s} (x) = \ sum_ {i = 1} ^ {n} c_i \ mathbf {z} _i (x) + \ mathbf {p} (x).

Une solution particulière de l'équation inhomogène se trouve sous la méthode des coefficients indéterminés ou Procédé de variation de paramètres.

Systèmes fondamentaux pour les équations homogènes à coefficients constants

Pour un système d'équations différentielles linéaires homogènes à coefficients constants

\ Mathbf {y} ^ '(x) = \ mathbf {A} \ mathbf {y} (x)

nous pouvons explicitement construire un système fondamental. Le système peut être écrite comme une équation différentielle matrice

\ Mathbf {Y} ^ '= \ mathbf {A} \ mathbf {Y}

avec une solution comme matrice exponentielle

e ^ {x \ mathbf {A}}

qui est une matrice fondamentale de l'équation différentielle d'origine. Pour calculer explicitement cette expression nous transformons A en premier Réduction de Jordan

e ^ {x \ mathbf {A}} = e ^ {x \ mathbf {C} ^ {- 1} \ mathbf {J} \ mathbf {C} ^ {1}} = \ mathbf {C} ^ {- 1 } e ^ {x \ mathbf {J}} \ mathbf {C} ^ {1}

puis évaluer la Blocs de Jordan

J_i = \ begin {bmatrix} \ lambda_i & 1 & \; & \; \\ \; & \ & Ddots \ ddots & \; \\ \; & \; & \ & Ddots 1 \\ \; & \; & \; & \ Lambda_i \ end {} bmatrix

de J séparément en tant que

e ^ {x \ mathbf {}} J_i = e ^ {\ lambda_i x} \ begin {} bmatrix 1 & x & \ frac {x ^ 2} {2} \ & points et \ frac {x ^ {n-1 }} {(n-1)} \\ \!; & \ & Ddots \ ddots & \ & ddots \ vdots \\ \; & \; & \ Ddots & \ & ddots \ frac {x ^ 2} {2} \\ \; & \; & \; & \ & Ddots x \\ \; & \; & \; & \; & 1 \ end {} bmatrix.

Théories de EDO

Solutions singulières

La théorie de la solutions singulières des équations différentielles ordinaires et partielles était un sujet de recherche à partir du moment de Leibniz, mais seulement depuis le milieu du XIXe siècle at-elle reçoivent une attention particulière. Un travail précieux, mais peu connu sur le sujet est celle de Houtain (1854). Darboux (à partir de 1873) était un chef de file dans la théorie et dans l'interprétation géométrique de ces solutions, il a ouvert un champ qui a été travaillé par divers auteurs, notamment Casorati et Cayley. Pour ce dernier est due (1872) la théorie de solutions singulières des équations différentielles du premier ordre comme acceptée vers 1900.

Réduction à quadratures

La tentative primitive dans le traitement des équations différentielles avait en vue une réduction quadratures. Comme il avait été l'espoir de algébristes du XVIIIe siècle pour trouver une méthode pour résoudre l'équation générale de la 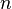n e degré, donc ce était l'espoir d'analystes de trouver une méthode générale pour l'intégration de toute équation différentielle. Gauss (1799) a montré, cependant, que l'équation différentielle rencontre ses limites très bientôt moins nombres complexes sont introduits. D'où les analystes ont commencé à remplacer l'étude des fonctions, ouvrant ainsi un champ nouveau et fertile. Cauchy était le premier à apprécier l'importance de ce point de vue. Par la suite, la véritable question était d'être, pas si une solution est possible au moyen de fonctions connues ou leurs intégrales, mais de savoir si une équation différentielle donnée suffit pour la définition d'une fonction de la variable indépendante ou des variables, et si oui, quelles sont les propriétés caractéristiques de cette fonction.

Théorie fuchsien

Deux mémoires par Fuchs (Crelle, 1866, 1868), a inspiré une nouvelle approche, par la suite élaboré par Thomé et Frobenius. Collet a été un contributeur de premier plan à partir de 1869, bien que sa méthode d'intégration d'un système non-linéaire a été communiquée à Bertrand en 1868. Clebsch (1873) a attaqué la théorie long de lignes parallèles à celles suivies dans sa théorie de Intégrales abéliennes. Comme celui-ci peuvent être classés en fonction des propriétés de la courbe fondamentale qui reste inchangé par une transformation rationnelle, afin de Clebsch proposé de classer les fonctions transcendantes définies par les équations différentielles selon les propriétés invariantes des surfaces correspondantes F = 0 sous rationnelle une -à-une transformations.

La théorie de Lie

De 1870 Le travail de Lie mis la théorie des équations différentielles sur une base plus satisfaisante. Il a montré que les théories de l'intégration des mathématiciens âgés peuvent, par l'introduction de ce qu'on appelle aujourd'hui groupes de Lie, être soumis à une source commune; et que les équations différentielles ordinaires qui admettent même transformations infinitésimales présentent des difficultés d'intégration comparables. Il a également souligné l'objet de transformations de contact (Berührungstransformationen).

Théorie de Sturm-Liouville

Théorie de Sturm-Liouville est une méthode générale pour la résolution des équations du second ordre linéaires à coefficients variables.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Ordinary_differential_equation&oldid=198824413 "