Série de Taylor
Renseignements généraux
Arrangeant une sélection Wikipedia pour les écoles dans le monde en développement sans internet était une initiative de SOS Enfants. Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

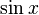 et approximations Taylor, polynômes de degré 1, 3, 5, 7, 9, 11 et 13.
et approximations Taylor, polynômes de degré 1, 3, 5, 7, 9, 11 et 13. 
En mathématiques , la série de Taylor est une représentation d'une fonction comme une infinie somme de termes calculées à partir des valeurs de ses dérivés en un seul point. Il peut être considéré comme la limite des polynômes de Taylor . Série de Taylor sont nommés en l'honneur de Mathématicien anglais Brook Taylor. Si la série utilise les dérivés à zéro, la série est aussi appelé une série de Maclaurin, nommé d'après Mathématicien écossais Colin Maclaurin.
Définition
La série de Taylor d'un réel ou complexe fonction f (x) qui est infiniment différentiables dans un voisinage d'un réel ou complexe d'un nombre, ce est la série de puissance
qui, dans une forme plus compacte peut être écrit comme
où n! est la factorielle de n et f (n) (a) désigne la nième dérivée de f au point a; le dérivé de zéro de f est défini comme étant lui-même et f (x - a) et 0 0! sont tous deux définis comme une.
Souvent f (x) est égale à sa série de Taylor évalués à x pour tout x assez voisin de a. Ce est la principale raison pour laquelle la série de Taylor sont importants.
Dans le cas particulier où  , La série est aussi appelé une série de Maclaurin.
, La série est aussi appelé une série de Maclaurin.
Exemples
La série de Maclaurin pour tout polynôme est le polynôme lui-même.
La série de Maclaurin pour 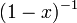 est le série géométrique
est le série géométrique
de sorte que la série de Taylor pour  à
à  est
est
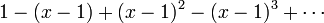 .
.
En intégrant le dessus de série de Maclaurin nous trouvons la série de Maclaurin pour 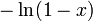 Où
Où  désigne le logarithme naturel :
désigne le logarithme naturel :
et la série correspondante pour Taylor  à
à  est
est
 .
.
La série de Maclaurin pour la fonction exponentielle  à
à  est
est
 .
.
L'expansion ci-dessus tient parce que le dérivé de  est aussi
est aussi  et
et  égale 1. Cela laisse les termes
égale 1. Cela laisse les termes  dans le numérateur et n! dans le dénominateur pour chaque terme de la somme infinie.
dans le numérateur et n! dans le dénominateur pour chaque terme de la somme infinie.
Convergence


La série de Taylor ne doit pas en général être un série convergente, mais il est souvent. La limite d'une série convergente Taylor ne doit pas en général être égale à la valeur de la fonction f (x), mais il est souvent. Si f (x) est égale à sa série de Taylor dans un d'un quartier, il est dit être analytique dans ce quartier. Si f (x) est égale à sa série de Taylor partout où elle est appelée ensemble. La fonction exponentielle  et les fonctions trigonométriques sinus et cosinus sont des exemples de fonctions entières. Des exemples de fonctions qui ne sont pas ensemble comprennent le logarithme , la fonction trigonométrique tangente, et son inverse arctan. Pour ces fonctions la série de Taylor ne en ont pas converger si x est loin d'être une.
et les fonctions trigonométriques sinus et cosinus sont des exemples de fonctions entières. Des exemples de fonctions qui ne sont pas ensemble comprennent le logarithme , la fonction trigonométrique tangente, et son inverse arctan. Pour ces fonctions la série de Taylor ne en ont pas converger si x est loin d'être une.
Une série de Taylor peut être utilisé pour calculer la valeur d'une fonction entière en tout point, si la valeur de la fonction, et de tous ses dérivés, sont connus en un seul point. Usages de la série de Taylor pour les fonctions entières comprennent:
- Les sommes partielles (les polynômes de Taylor ) de la série peuvent être utilisés comme approximations de la fonction entière. Ces approximations sont bonnes si elles sont suffisamment nombreux termes sont inclus.
- La représentation de la série simplifie de nombreuses preuves mathématiques .
Sur la photo à droite est une approximation précise de sin (x) autour du point a = 0. La courbe rose est un polynôme de degré de sept:
 .
.
L'erreur dans cette approximation ne est pas supérieure  . En particulier, pour
. En particulier, pour  , L'erreur est inférieure à 0,000003.
, L'erreur est inférieure à 0,000003.
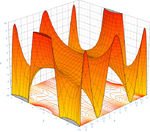
En revanche, est également montré une image de la fonction log (1 + x) et certains de ses polynômes de Taylor autour d'un = 0 Ces approximations convergent vers la fonction que dans la région -1 <x ≤ 1. en dehors de cette région la plus élevée degré polynômes de Taylor sont des approximations pire pour la fonction. Ceci est un exemple de Phénomène de Runge.
Le théorème de Taylor donne une variété de limites générales de la taille de l'erreur dans  engagés dans l'approximation d'une fonction par son ordre n polynôme de Taylor.
engagés dans l'approximation d'une fonction par son ordre n polynôme de Taylor.
Histoire
Le Philosophe Pythagore Zeno examiné le problème des additionnant une série infinie d'obtenir un résultat fini, mais l'a rejeté comme une impossibilité: le résultat était Le paradoxe de Zénon. Plus tard, Aristote a proposé une résolution philosophique du paradoxe, mais le contenu mathématique était apparemment en suspens jusqu'à repris par Démocrite et puis Archimède . Ce est grâce à Archimède de méthode de l'épuisement qu'un nombre infini de subdivisions progressistes pourrait être réalisée pour obtenir un résultat trigonométrique finie. Liu Hui employé indépendamment une méthode similaire plusieurs siècles plus tard.
Dans le 14ème siècle , les premiers exemples de l'utilisation de méthodes de la série et étroitement apparentés ont été donnés par Taylor Madhava de Sangamagrama. Bien que aucune trace de son travail survit, écrits de ultérieures mathématiciens indiens suggèrent qu'il a trouvé un certain nombre de cas particuliers de la série de Taylor, y compris ceux pour les fonctions trigonométriques de sinus, cosinus, tangente , et arctangente. Le École du Kerala encore élargi ses œuvres avec divers développements en série et approximations rationnelles jusqu'à ce que le 16ème siècle .
Dans le 17ème siècle , James Gregory a également travaillé dans ce domaine et a publié plusieurs séries de Maclaurin. Ce ne est que 1715 cependant qu'une méthode générale pour la construction de ces séries pour toutes les fonctions pour lesquelles ils existent a finalement été fournis par Brook Taylor, après que les séries sont maintenant nommés.
La série de Maclaurin a été nommé d'après Colin Maclaurin, professeur à Edimbourg, qui a publié le cas particulier du résultat Taylor dans le 18ème siècle.
Propriétés
Si cette série converge pour tout x dans l'intervalle (a - r, a + r) et la somme est égale à f (x), alors la fonction f (x) est dit être analytique dans l'intervalle (a - r, a + r). Si cela est vrai pour tout r, alors la fonction est dit être un toute fonction. Pour vérifier si la série converge vers f (x), on utilise normalement des estimations pour la durée du reste du Théorème de Taylor . Une fonction est analytique si et seulement si elle peut être représentée comme une série de puissances ; les coefficients de cette série de puissance sont alors nécessairement celles indiquées dans la formule ci-dessus en série de Taylor.
L'importance d'une telle représentation de la série de puissance est au moins quatre fois. Tout d'abord, la différenciation et l'intégration de la série de puissance peuvent être effectuées terme à terme et est donc particulièrement facile. Deuxièmement, un fonction analytique peut être étendue à un unique fonction holomorphe définie sur un disque ouvert dans le plan complexe , ce qui rend l'ensemble des machines analyse complexe disponible. En troisième lieu, la série (tronqué) peut être utilisé pour calculer des valeurs de fonction environ (souvent par refonte du polynôme dans la Chebyshev forme et l'évaluation avec le Algorithme Clenshaw).
Quatrièmement, les opérations algébriques peuvent souvent être fait beaucoup plus facilement sur la représentation de la série de puissance; par exemple, la preuve la plus simple de La formule d'Euler utilise les développements en série de Taylor pour sinus, cosinus, et les fonctions exponentielles. Ce résultat est d'une importance fondamentale dans des domaines tels que analyse harmonique.
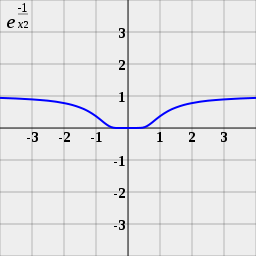
Notez qu'il existe des exemples de fonctions infiniment différentiables f (x) dont la série Taylor convergent, mais ne sont pas égale à f (x). Par exemple, la fonction ponctuelle définie par f (x) = e -1 / m² x si x ≠ 0 et f (0) = 0 est un exemple d'un fonction lisse non-analytique. Tous ses dérivés à x = 0 sont à zéro, de sorte que la série de Taylor de f (x) à 0 est de zéro partout, même si la fonction ne est pas nul pour tout x ≠ 0. Cette pathologie particulière ne afflige pas en série de Taylor analyse complexe. Là, la zone de convergence d'une série de Taylor est toujours un disque dans le plan complexe (éventuellement avec rayon 0), et où la série de Taylor converge, on converge vers la valeur de la fonction. Notez que e -1 / z ² ne approchez pas 0 en z se approche de 0 long de l'axe imaginaire, d'où cette fonction ne est pas continue en fonction sur le plan complexe.
Étant donné que chaque séquence de nombres réels ou complexes peut apparaître comme coefficients de la série de Taylor d'une fonction différenciable en continu défini sur la ligne réelle, le rayon de convergence d'une série de Taylor peut être égal à zéro. Il ya même infiniment fonctions différentiables définies sur la droite réelle dont la série Taylor avoir un rayon de convergence 0 partout.
Certaines fonctions ne peuvent pas être écrit comme série de Taylor parce qu'ils ont un singularité; dans ces cas, on peut souvent obtenir encore un développement en série si l'on admet aussi puissances négatives de la variable x; voir Laurent série. Par exemple,  peut se écrire comme une série de Laurent.
peut se écrire comme une série de Laurent.
Le Méthode Parker-Sochacki est une avancée récente à trouver série de Taylor qui sont des solutions aux équations différentielles . Cet algorithme est une extension de la Itération Picard.
Liste des séries de Taylor de certaines fonctions communes
Plusieurs extensions importantes de la série de Maclaurin suivent. Tous ces développements sont valables pour les arguments complexes  .
.
Fini série géométrique:
Série géométrique infinie:
Des variantes de la série géométrique infinie:
Série binomiale (comprend la racine carrée pour α = 1/2 et la série géométrique infinie pour α = -1):

- avec généralisées coefficients binomiaux
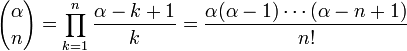
Les fonctions trigonométriques :
- où le B s sont Nombres de Bernoulli.
Fonctions hyperboliques:
La fonction W de Lambert:
Les nombres  apparaissant dans les expansions de sommation de tan (x) et tanh (x) sont les Nombres de Bernoulli. Le
apparaissant dans les expansions de sommation de tan (x) et tanh (x) sont les Nombres de Bernoulli. Le  dans l'expansion de s (x) sont Nombres d'Euler.
dans l'expansion de s (x) sont Nombres d'Euler.
Calcul de la série de Taylor
Il existe plusieurs méthodes pour le calcul de la série de Taylor d'un grand nombre de fonctions. On peut tenter d'utiliser la série de Taylor en l'état et généraliser la forme des coefficients, ou on peut utiliser des manipulations telles que la substitution, multiplication ou division, addition ou soustraction des séries de Taylor standard pour construire la série de Taylor d'une fonction, en vertu de la série Taylor étant série de puissance. Dans certains cas, on peut aussi calculer la série de Taylor en appliquant de façon répétée intégration par parties. Particulièrement pratique est l'utilisation de systèmes d'algèbre informatique pour calculer série de Taylor.
Premier exemple
Calculer la 7 ème degré Maclaurin polynomiale de la fonction
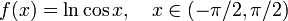 .
.
Premièrement, réécrire la fonction comme
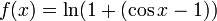 .
.
Nous avons pour le logarithme naturel (en utilisant le notation O grande)
et pour la fonction cosinus
Le développement en série de celui-ci a un zéro terme constant, ce qui nous permet de substituer la deuxième série dans le premier et d'omettre facilement termes d'ordre plus élevé que le 7 ème degré en utilisant la notation grand O:
Depuis le cosinus est un même fonction, les coefficients pour toutes les puissances impaires x, x, x 3 x 5, 7,. . . doivent être de zéro.
Deuxième exemple
Supposons que nous voulons la série de Taylor à 0 de la fonction
 .
.
Nous avons pour la fonction exponentielle
et, comme dans le premier exemple,
Supposons que la série de puissance est
Puis multiplication par le dénominateur et la substitution de la série des rendements de cosinus
Collecte les termes jusqu'à quatrième rendements de l'ordre
La comparaison avec les coefficients de la série ci-dessus pour la fonction exponentielle donne la série de Taylor désiré
 .
.
Série de Taylor que les définitions
Classiquement, les fonctions ci-dessus sont définis par une propriété qui détient pour eux. Par exemple, la fonction exponentielle est définie comme étant la fonction qui est égale à sa propre dérivé. Toutefois, analyse récursive, fonctions doit être défini par des algorithmes plutôt que des propriétés, de sorte que les développements de Taylor ci-dessus sont utilisés comme définitions primaires plutôt que des résultats dérivés. Ce est également susceptible d'être le cas dans les implémentations logicielles des fonctions.
Utilisation série de Taylor, on peut définir des fonctions d'analyse des matrices et des opérateurs, tels que matrice exponentielle ou matrice logarithme.
Série de Taylor en plusieurs variables
La série de Taylor peut également être généralisé à des fonctions de plus d'une variable avec

 .
.
Par exemple, pour une fonction dépendant de deux variables x et y, la série de Taylor de deuxième ordre par rapport au point (a, b) est:
où les indices représentent le respectif dérivées partielles.
Un second ordre développement en série de Taylor d'une fonction scalaire à valeur supérieure à une variable peut être écrit sous la forme compacte
où 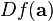 est le gradient et
est le gradient et  est le Hessien. L'application de la Multi-indice de la série de Taylor pour plusieurs variables devient
est le Hessien. L'application de la Multi-indice de la série de Taylor pour plusieurs variables devient
en pleine analogie avec le cas seule variable.
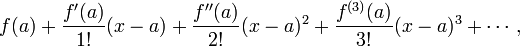
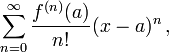

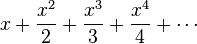

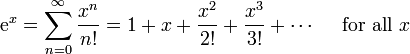


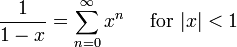

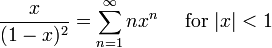
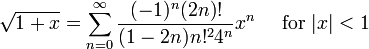
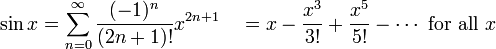




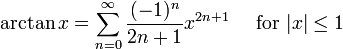




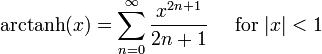


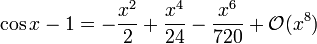

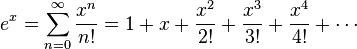
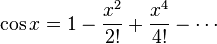
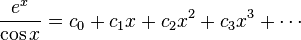




![+ \ Frac {1} {2!} \ Left [f_ {xx} (a, b) (xa) ^ 2 + 2f_ {xy} (a, b) (xa) (YB) + f_ {aa} (un , b) (YB) ^ 2 \ right] \!](../../images/96/9601.png)