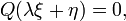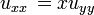Équation aux dérivées partielles
Saviez-vous ...
SOS Enfants, un organisme de bienfaisance de l'éducation , a organisé cette sélection. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
En mathématiques , équations aux dérivées partielles (PDE) sont un type de l'équation différentielle , soit un relation impliquant un inconnu fonction (ou fonctions) de plusieurs variables indépendantes et de son (resp.) de leur dérivées partielles par rapport aux variables. Équations aux dérivées partielles sont utilisées pour formuler, et ainsi aider à la solution de problèmes impliquant des fonctions de plusieurs variables; telles que la propagation des sons ou de la chaleur , électrostatique, l'électrodynamique, l'écoulement du fluide, élasticité. Fait intéressant, les phénomènes physiques apparemment distinctes peuvent avoir des formulations mathématiques identiques, et donc être régi par la même dynamique sous-jacente.
Introduction
Une équation différentielle partielle est relativement simple
Cette relation implique que les valeurs u (x, y) sont indépendants de x. D'où la solution générale de cette équation est
où f est une fonction arbitraire (différentiable) de y. L'analogue équation différentielle ordinaire est
ce qui a pour solution
où c est ne importe quel valeur constante (indépendant de x). Ces deux exemples montrent que des solutions générales d'équations différentielles ordinaires impliquent constantes arbitraires, mais les solutions d'équations aux dérivées partielles impliquent des fonctions arbitraires. Une solution d'une équation différentielle partielle est généralement pas uniques; conditions supplémentaires doivent généralement être spécifiés sur la limite de la région où la solution est définie. Par exemple, dans l'exemple simple ci-dessus, la fonction  peut être déterminé si
peut être déterminé si  est spécifié sur la ligne
est spécifié sur la ligne  .
.
Existence et unicité
Bien que la question de l'existence et l'unicité de solutions d'équations différentielles ordinaires a une réponse très satisfaisante avec le Théorème de Cauchy-Lipschitz, qui est loin d'être le cas pour les équations aux dérivées partielles. Il ya un théorème général (la Théorème de Cauchy-Kovalevskaya) qui indique que le Problème de Cauchy pour toute équation différentielle partielle qui est analytique dans la fonction inconnue et ses dérivés ont une solution analytique unique. Bien que ce résultat peut apparaître pour régler l'existence et l'unicité de solutions, il ya des exemples d'équations aux dérivées partielles linéaires dont les coefficients ont dérivés de toutes les commandes (qui sont cependant pas analytique), mais qui ne ont pas de solutions à tous: voir Lewy (1957). Même si la solution d'une équation différentielle partielle existe et est unique, elle peut néanmoins avoir des propriétés indésirables.
Un exemple de comportement pathologique est la séquence des problèmes de Cauchy (n) dépendant de la Équation de Laplace
avec conditions initiales
où n est un entier. La dérivée de u par rapport à y se approche de 0 uniformément en x lorsque n augmente, mais la solution est
Cette solution tend vers l'infini, si nx est pas un multiple entier de π pour chaque valeur de y non nul. Le problème de Cauchy pour l'équation de Laplace est appelée mal posé ou non bien posé, car la solution ne dépend pas de manière continue sur les données du problème. Ces problèmes mal posés ne sont généralement pas satisfaisante pour les applications physiques.
Notation et exemples
Dans PDE, il est courant pour désigner dérivées partielles à l'aide des indices. C'est:
Surtout dans (mathématique) la physique, on préfère souvent usage de del (qui en coordonnées cartésiennes est écrit  pour les dérivées spatiales et un point
pour les dérivées spatiales et un point  pour les dérivés de temps, par exemple, pour écrire le équation d'onde (voir ci-dessous)
pour les dérivés de temps, par exemple, pour écrire le équation d'onde (voir ci-dessous)
 (Notation mathématique)
(Notation mathématique)
 (Notation de la physique)
(Notation de la physique)
Equation de la chaleur dans une dimension de l'espace
L'équation de conduction de la chaleur dans une dimension pour un corps homogène a la forme
où u (t, x) est la température, et α est une constante positive qui décrit la vitesse de diffusion. Le problème de Cauchy pour cette équation consiste à spécifier 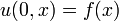 , Où f (x) est une fonction arbitraire.
, Où f (x) est une fonction arbitraire.
Solutions générales de l'équation de la chaleur peuvent être trouvés par le procédé de séparation des variables. Quelques exemples figurent dans le article équation de la chaleur. Ils sont des exemples de Séries de Fourier pour périodique f et Transformées de Fourier pour non périodique f. Utilisation de la transformée de Fourier, une solution générale de l'équation de la chaleur a la forme
où F est une fonction arbitraire. Pour satisfaire à la condition initiale, F est donnée par la transformée de Fourier de f, ce est-
Si f représente un très petit mais intense source de chaleur, puis l'intégrale précédente peut être approchée par la la distribution delta, multiplié par la résistance de la source. Pour une source dont la force est normalisée à 1, le résultat est
et la solution résultante de l'équation de la chaleur est
C'est un Gaussienne intégrante. Elle peut être évaluée à obtenir
Ce résultat correspond à une densité de probabilité normale pour x avec une moyenne de 0 et de variance t 2α. L'équation de la chaleur et similaires équations de diffusion sont des outils utiles pour étudier des phénomènes aléatoires.
équation d'onde dans une dimension spatiale
Le équation d'onde est une équation pour une fonction inconnue u (t, x) de la forme
Ici u peut décrire le déplacement d'une chaîne étirée à partir de l'équilibre, ou la différence de pression d'air dans un tube, ou l'amplitude d'un champ électromagnétique dans un tube, et c est un nombre qui correspond à la vitesse de l'onde. Le problème de Cauchy pour cette équation consiste à prescrire le déplacement initial et la vitesse d'une chaîne ou un autre support:
où f et g sont des fonctions arbitraires donnés. La solution de ce problème est donnée par la formule de d'Alembert:
Cette formule implique que la solution à (t, x) ne dépend que des données sur le segment de ligne initial qui est coupé par le courbes caractéristiques
qui sont tirés vers l'arrière de ce point. Ces courbes correspondent à des signaux qui se propagent à la vitesse c avant et en arrière. Inversement, l'influence des données à ne importe quel point sur la ligne initiale donnée se propage à la vitesse finie c: il n'y a pas d'effet en dehors d'un triangle par ce point dont les côtés sont courbes caractéristiques. Ce problème est très différent de la solution de l'équation de chaleur, où l'effet d'un source ponctuelle apparaît (avec faible amplitude) instantanément à chaque point de l'espace. La solution donnée ci-dessus est également valable si t est négatif, et la formule explicite montre que la solution dépend en douceur sur les données: à la fois vers l'avant et vers l'arrière problèmes de Cauchy pour l'équation d'onde sont bien posées.
Ondes sphériques
Ondes sphériques sont des ondes dont l'amplitude ne dépend que de la distance r à partir d'un central radial source ponctuelle. Pour ces ondes, l'équation d'onde tridimensionnelle prend la forme
Ceci est équivalent à
et par conséquent la quantité ru satisfait à l'équation d'onde unidimensionnelle. Par conséquent, une solution générale pour les ondes sphériques a la forme
où F et G sont des fonctions totalement arbitraires. Rayonnement d'une antenne correspond au cas où G est identiquement nulle. Ainsi la forme d'onde transmise par une antenne a pas de distorsion dans le temps: le seul facteur de distorsion est 1 / r. Cette fonction de propagation des ondes non faussée ne est pas présent se il ya deux dimensions spatiales.
Équation de Laplace en deux dimensions
Le Équation de Laplace pour une fonction inconnue de deux variables φ est de la forme
Les solutions de l'équation de Laplace sont appelés fonctions harmoniques.
Connexion avec des fonctions
Les solutions de l'équation de Laplace sont intimement liées à des fonctions analytiques d'une variable complexe (fonctions holomorphes aka): les parties réelle et imaginaire d'une fonction analytique sont des fonctions harmoniques conjugués: ils ont tous deux satisfont l'équation de Laplace, et leurs gradients sont orthogonaux. Si f = u + iv, le Cauchy-Riemann équations Etat qui
et il se ensuit que
A l'inverse, compte tenu de toute fonction harmonique, ce est la partie réelle d'une fonction analytique, au moins localement. Les détails sont donnés dans Équation de Laplace.
Un problème typique de la valeur limite
Un problème typique pour l'équation de Laplace est de trouver une solution qui satisfait des valeurs arbitraires sur la limite d'un domaine. Par exemple, nous pouvons rechercher une fonction harmonique qui prend les valeurs u (θ) sur un cercle de rayon d'un. La solution est donnée par Poisson:
Pétrovsky (1967, p. 248) montre comment cette formule peut être obtenu en additionnant une série de Fourier de φ. Si r <1, les dérivés de φ peuvent être calculées en différenciant sous le signe, et on peut vérifier que φ est analytique, même si u est continue mais pas nécessairement différentiables. Ce comportement est typique des solutions de équations aux dérivées partielles elliptiques: les solutions peuvent être beaucoup plus lisse que les données sur les limites. Ceci est en contraste avec les solutions de la équation d'onde, et plus générale équations aux dérivées partielles hyperboliques, qui ont généralement pas plus de dérivés que les données.
Équation d'Euler-Tricomi
Le Équation d'Euler-Tricomi est utilisé dans l'enquête de écoulement transsonique. C'est
équation d'advection
Le équation d'advection décrit le transport d'un scalaire conservée 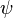 dans un champ de vitesse
dans un champ de vitesse  . C'est:
. C'est:
Si le champ de vitesse est solénoïdal (ce est-  ), L'équation peut être simplifiée pour
), L'équation peut être simplifiée pour
L'une équation d'advection de flux constant dimensions 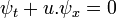 (Où
(Où 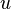 est constant) est communément dénommé problème porcherie. Si
est constant) est communément dénommé problème porcherie. Si 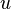 ne est pas constant et égal à
ne est pas constant et égal à 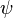 l'équation est appelée Équation de Burgers.
l'équation est appelée Équation de Burgers.
L'équation de Ginzburg-Landau
Le L'équation de Ginzburg-Landau est utilisé dans la modélisation de la supraconductivité . C'est
où 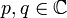 et
et  sont des constantes et
sont des constantes et  est l'unité imaginaire.
est l'unité imaginaire.
L'équation Dym
Le Dym équation est nommé pour Dym Harry et se produit à l'étude de solitons. C'est
D'autres exemples
Le Équation de Schrödinger est un PDE au cœur de non-relativistes mécanique quantique . Dans le Approximation BKW ce est le Équation de Hamilton-Jacobi.
Sauf pour l'équation Dym et l'équation de Ginzburg-Landau, les équations ci-dessus sont linéaires dans le sens où elles peuvent être écrites sous la forme Au = f pour une donnée linéaire opérateur A et une fonction donnée f. Autres équations non linéaires importants comprennent les équations de Navier-Stokes décrivant l'écoulement des fluides, et Einstein équations du champ de la relativité générale .
Méthodes pour résoudre les EDP
Procédé selon la séparation des variables donnera des solutions particulières d'un PDE linéaire sur des domaines très simples tels que des rectangles qui peuvent satisfaire les conditions initiales ou limites. Parce que toute superposition de solutions d'un nouveau PDE linéaire est une solution, les solutions particulières peuvent ensuite être combinés pour obtenir des solutions plus générales. Si le domaine est fini ou périodique, une somme infinie de solutions telles qu'un série de Fourier est appropriée, mais une intégrale de solutions telles que la intégrale de Fourier est généralement requise pour les domaines infinite. La solution pour une source ponctuelle de l'équation de la chaleur donnée ci-dessus est un exemple d'utilisation d'une intégrale de Fourier.
Problèmes de valeur initiale de limite
Beaucoup de problèmes de physique mathématique sont formulés comme des problèmes de valeur initiale de limites.
Corde vibrante
Si la chaîne est tendue entre deux points où x = 0 et x = L et U désigne l'amplitude du déplacement de la chaîne, puis u satisfait l'équation des ondes à une dimension dans la région où 0 <x <L et t est illimité . Depuis la chaîne est attaché aux extrémités, u doit également satisfaire les conditions aux limites
ainsi que les conditions initiales
Procédé de séparation des variables de l'équation d'onde
conduit à des solutions de la forme
où
où la constante k doit être déterminée. Les conditions aux limites impliquerait alors que X est un multiple du péché kx, et k doivent avoir la forme
où n est un entier. Chaque terme de la somme correspond à un mode de vibration de la corde. Le mode avec n = 1 est appelé le mode fondamental, et les fréquences des autres modes sont tous des multiples de cette fréquence. Ils forment la Overtone série de la chaîne, et ils sont la base de l'acoustique musicale. Les conditions initiales peuvent alors être remplies par f et g soit comme des sommes infinies de ces modes. Instruments à vent correspondent généralement à des vibrations d'une colonne d'air avec une extrémité ouverte et une extrémité fermée. Les conditions aux limites correspondantes sont
Procédé de séparation des variables peut également être appliquée dans ce cas, et cela conduit à une série d'harmoniques impairs.
Le problème de ce type général est résolu en Théorie de Sturm-Liouville.
Membrane vibrante
Si une membrane est tendue sur une courbe C qui forme la limite d'un domaine D dans le plan, ses vibrations sont régies par l'équation des ondes
si t> 0 et (x, y) est en développement. La condition limite est 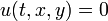 si
si 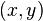 est le
est le 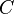 . Procédé de séparation des variables conduit à la forme
. Procédé de séparation des variables conduit à la forme
qui à son tour doit satisfaire
Cette dernière équation est appelé le Helmholtz équation. La constante k doit être déterminée afin de permettre un v non négligeable pour satisfaire la condition aux limites sur C. De telles valeurs de k 2 sont appelés les valeurs propres du Laplacien en D, et les solutions sont associées les fonctions propres du Laplacien par D. La théorie de Sturm-Liouville peut être étendue à ce problème elliptique valeur propre (Jost, 2002).
Il n'y a pas en général de méthodes applicables pour résoudre des équations aux dérivées partielles non linéaires. Pourtant, existence et unicité des résultats (tels que le Théorème de Cauchy-Kowalevski) sont souvent possible, comme le sont les preuves de propriétés qualitatives et quantitatives importantes de solutions (obtenir ces résultats est une partie importante de l'analyse ). Solution informatique pour les équations aux dérivées partielles non linéaires, le Méthode split-étape, exister pour équations spécifiques comme l'équation de Schrödinger non linéaire.
Néanmoins, certaines techniques peuvent être utilisées pour plusieurs types d'équations. Le h-principe est la méthode la plus puissante pour résoudre équations sousdéterminés. Le Théorie Riquier-Janet est une méthode efficace pour obtenir des informations sur de nombreux analytique systèmes surdéterminés.
Le Procédé de caractéristiques ( Similarité méthode de transformation) peut être utilisé dans certains cas très particuliers pour résoudre des équations aux dérivées partielles.
Dans certains cas, une PDE peut être résolu grâce à une analyse de perturbation, dans lequel la solution est considérée comme une correction à une équation d'une solution connue. Alternatives sont techniques d'analyse numérique de la simple schémas aux différences finies à la plus mature multigrille et méthodes d'éléments finis. De nombreux problèmes intéressants dans la science et l'ingénierie sont résolus de cette manière en utilisant des ordinateurs , parfois haute performance superordinateurs.
Classification
Quelques équations aux dérivées partielles linéaire, second ordre peuvent être classés comme parabolique, hyperbolique ou elliptique. D'autres, comme le Équation d'Euler-Tricomi ont différents types dans différentes régions. La classification fournit un guide pour se approprier conditions initiales et aux limites, et de la douceur des solutions.
Équations du second ordre
Supposant  , Le PDE générale de second ordre à deux variables indépendantes a la forme
, Le PDE générale de second ordre à deux variables indépendantes a la forme
où les coefficients A, B, C etc. peut dépendre de x et y. Cette forme est analogue à l'équation d'une section conique:
Tout comme on classe les sections coniques en parabolique, hyperbolique et elliptique sur la base du discriminant 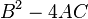 , La même chose peut être fait pour un PDE second ordre à un moment donné.
, La même chose peut être fait pour un PDE second ordre à un moment donné.
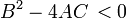 : Solutions de EDP elliptiques sont aussi lisses que les coefficients permettent, à l'intérieur de la région où l'équation et les solutions sont définis. Par exemple, les solutions de l'équation de Laplace sont analytiques dans le domaine où ils sont définis, mais les solutions peuvent prendre des valeurs limites qui ne sont pas lisses. Le mouvement d'un fluide à des vitesses subsoniques peut être approchée avec EDP elliptiques, et l'équation d'Euler-Tricomi est elliptique où x <0.
: Solutions de EDP elliptiques sont aussi lisses que les coefficients permettent, à l'intérieur de la région où l'équation et les solutions sont définis. Par exemple, les solutions de l'équation de Laplace sont analytiques dans le domaine où ils sont définis, mais les solutions peuvent prendre des valeurs limites qui ne sont pas lisses. Le mouvement d'un fluide à des vitesses subsoniques peut être approchée avec EDP elliptiques, et l'équation d'Euler-Tricomi est elliptique où x <0.  qui sont les équations: parabolique à chaque point peut être transformé en une forme analogue à l'équation de la chaleur par un changement de variables indépendantes. Solutions lisser les variables transformées de temps augmente. L'équation d'Euler-Tricomi a type parabolique sur la ligne où x = 0.
qui sont les équations: parabolique à chaque point peut être transformé en une forme analogue à l'équation de la chaleur par un changement de variables indépendantes. Solutions lisser les variables transformées de temps augmente. L'équation d'Euler-Tricomi a type parabolique sur la ligne où x = 0.  : équations hyperboliques conservent tous les discontinuités de fonctions ou de dérivés dans les données initiales. Un exemple est le équation d'onde. Le mouvement d'un fluide à des vitesses supersoniques peut être approchée avec les systèmes hyperboliques, et l'équation d'Euler-Tricomi est hyperbolique où x> 0.
: équations hyperboliques conservent tous les discontinuités de fonctions ou de dérivés dans les données initiales. Un exemple est le équation d'onde. Le mouvement d'un fluide à des vitesses supersoniques peut être approchée avec les systèmes hyperboliques, et l'équation d'Euler-Tricomi est hyperbolique où x> 0.
Si il ya des variables indépendantes n X 1, X 2, ..., x n, une équation linéaire partielle différentiel général de second ordre a la forme
La classification dépend de la signature des valeurs propres de la matrice de coefficients.
- Elliptic: Les valeurs propres sont tous positifs ou négatifs.
- Antenne: Les valeurs propres sont tous positifs ou tous négatifs, sauf un qui est nul.
- Hyperbolique: Il ya une seule valeur propre négatif et tout le reste sont positifs, ou il ya une seule valeur propre positive et tout le reste sont négatifs.
- Ultrahyperbolic: Il ya plus d'une valeur propre positive et plus d'une valeur propre négative, et il n'y a pas de valeurs propres zéro. Il ne est que théorie limitée pour les équations ultrahyperbolic (Courant et Hilbert, 1962).
Systèmes d'équations du premier ordre et surfaces caractéristiques
La classification des équations aux dérivées partielles peut être étendue à des systèmes d'équations du premier ordre, où l'inconnue u est maintenant un vecteur à m composantes, et les matrices de coefficients  sont m par m matrices pour
sont m par m matrices pour  . L'équation différentielle partielle prend la forme
. L'équation différentielle partielle prend la forme
où le coefficient ν matrices A et le vecteur B peut dépendre de x et u. Si une hypersurface S est donnée dans la forme implicite
où φ a un gradient non nul, alors S est une surface caractéristique de l'opérateur L à un moment donné, si la forme caractéristique disparaît:
L'interprétation de cette condition géométrique est la suivante: si les données pour u sont prévues sur la surface S, alors il peut être possible de déterminer la dérivée normale de u sur S de l'équation différentielle. Si les données sur S et l'équation différentielle déterminer la dérivée normale de u sur S, alors S est non caractéristique. Si les données sur les S et l'équation différentielle ne déterminent pas la dérivée normale de u sur S, alors la surface est caractéristique, et l'équation différentielle limite les données sur S: l'équation différentielle est interne à S.
- Un système de premier ordre Lu = 0 est elliptique si aucune surface est caractéristique pour L: les valeurs de u sur S et l'équation différentielle déterminent toujours la dérivée normale de u sur S.
- Un système de premier ordre est hyperbolique à un point se il ya une surface S comme-spatiale avec ξ normale à ce point. Cela signifie que, compte tenu de tout vecteur non trivial orthogonal à η ξ, et un multiplieur scalaire λ, l'équation
a 1, λ 2, ..., λ m de m racines réelles. Le système est strictement hyperbolique si ces racines sont toujours distinctes. L'interprétation géométrique de cette condition est la suivante: la forme caractéristique Q (ζ) = 0 définit un cône (le cône normal) avec des coordonnées homogène ζ. Dans le cas hyperbolique, ce cône a m feuilles, et l'axe ζ = λ ξ se exécute dans ces feuilles: il ne coupe pas l'un d'eux. Mais lorsqu'il est déplacé depuis l'origine par η, cet axe croise chaque feuille. Dans le cas elliptique, le cône normal n'a pas de feuilles réels.
Équations de type mixte
Si un PDE a coefficients qui ne sont pas constant, il est possible qu'il ne appartenait à aucune de ces catégories, mais plutôt être de type mixte. Un exemple simple mais important, ce est l'équation d'Euler-Tricomi
qui est appelé elliptique-hyperbolique car il est elliptique dans la région x <0, hyperbolique dans la région x> 0, et parabolique dégénérée sur la ligne x = 0.


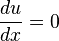

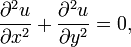


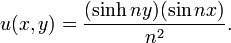
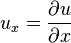

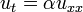
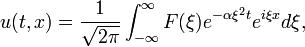

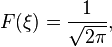


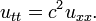


![u (t, x) = \ frac {1} {2} \ left [f (x-ct) + f (x + ct) \ right] + \ frac {1} {2c} \ {x int_-ct} ^ {x + ct} g (y) \, dy. \,](../../images/89/8985.png)

![u_ {tt} = c ^ 2 \ gauche [u_ {rr} + \ frac {2} {r} U_r \ right]. \,](../../images/89/8987.png)
![(Ru) _ {tt} = c ^ 2 \ left [(ru) _ {rr} \ right], \,](../../images/89/8988.png)
![u (t, r) = \ frac {1} {r} \ left [F (R-CT) + G (r + ct) \ right], \,](../../images/89/8989.png)
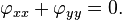
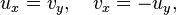

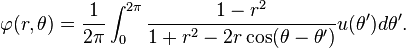

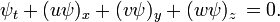
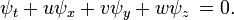






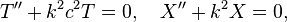
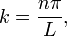
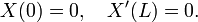
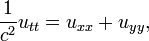

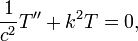
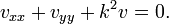
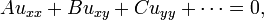
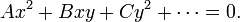


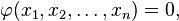
![Q \ left (\ frac {\ part \ varphi} {\ de x_1 partielle}, \ ldots, \ frac {\ part \ varphi} {\ de x_n partielle} \ right) = \ det \ left [\ sum _ {\ nu = 1 } ^ nA_ \ nu \ frac {\ partial \ varphi} {\ x_ partielle \ nu} \ right] = 0. \,](../../images/90/9030.png)