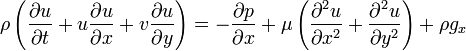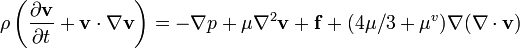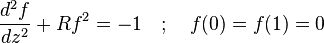Équations de Navier-Stokes
Saviez-vous ...
Cette sélection de wikipedia a été choisi par des bénévoles aidant les enfants SOS de Wikipedia pour cette sélection Wikipedia pour les écoles. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
| Mécanique des milieux continus |
|---|
 |
Lois
|
Mécanique des solides
|
|
Rhéologie
|
Les équations de Navier-Stokes, nommé d'après Claude-Louis Navier et George Gabriel Stokes, décrire le mouvement de substances fluides tels que les liquides et les gaz . Ces équations établissent que les changements dans la dynamique des volumes infimes de liquide sont tout simplement la somme de dissipation forces de viscosité (similaires à friction), changements dans la pression, la gravité et d'autres forces qui agissent à l'intérieur du fluide: une application de la deuxième loi de Newton à fluide.
Ils sont l'un des ensembles les plus utiles des équations parce qu'ils décrivent la physique d'un grand nombre de phénomènes d'intérêt économique et universitaire. Ils peuvent être utilisés pour modèle météo , les courants océaniques, les flux de l'eau dans un tuyau, l'écoulement autour d'un aérodynamique (aile), et le mouvement des étoiles à l'intérieur d'une galaxie . En tant que tel, ces équations dans les deux formes complets et simplifiés, sont utilisés dans la conception des avions et des voitures, l'étude de la circulation sanguine, la conception des centrales, l'analyse des effets de la pollution, etc. Couplé avec les équations de Maxwell qu'ils peuvent être utilisé pour modéliser et d'étude magnétohydrodynamique.
Les équations de Navier-Stokes sont également d'un grand intérêt dans un sens purement mathématique. Assez étonnamment, compte tenu de leur large éventail d'utilisations pratiques, les mathématiciens ne ont pas encore prouvé que dans trois solutions dimensions existent toujours ( existence), ou que, se ils existent, elles ne contiennent pas infinis, singularités ou des discontinuités (lissage). On les appelle les Navier-Stokes existence et régularité problèmes. Le Clay Mathematics Institute a appelé celui de la sept problèmes ouverts plus importantes en mathématiques, et a offert un prix $ 1.000.000 pour une solution ou un contre-exemple.
Les équations de Navier-Stokes sont des équations différentielles qui, contrairement équations algébriques, ne établissent pas explicitement une relation entre les variables d'intérêt (par exemple, la vitesse et pression). Au contraire, ils établissent des relations entre les taux de variation . Par exemple, les équations de Navier-Stokes pour simple cas d'un fluide idéale (non visqueux) peut indiquer que l'accélération (le taux de variation de vitesse ) est proportionnelle à la gradient (un type de dérivé multivariée) de pression.
Contrairement à ce qui est normalement vu dans mécanique des solides, les équations de Navier-Stokes dictent pas position, mais plutôt vitesse . Une solution des équations de Navier-Stokes se appelle un champ de champ de vitesse ou de l'écoulement, qui est une description de la vitesse du fluide en un point donné de l'espace et du temps. Une fois que le champ de vitesse est résolu pour, d'autres quantités d'intérêt (tels que le débit, la force de traînée, ou le chemin d'une «particule» de fluide aura) peuvent être trouvés.
Propriétés
Non-linéarité
Les équations de Navier-Stokes sont non linéaires équations aux dérivées partielles dans presque chaque situation réelle (exceptions comprennent un flux dimensionnelle et rampante flux). La non-linéarité rend la plupart des problèmes difficiles ou impossibles à résoudre et fait partie de la cause de turbulence.
La non-linéarité est due à accélération de convection, qui est associée à une accélération de la variation de la vitesse en fonction du poste. Par conséquent, tout écoulement par convection, si turbulent ou non, entraînera la non-linéarité, un exemple de convection mais laminaire (non turbulent) Flux serait le passage d'un fluide visqueux (par exemple l'huile) à travers une petite convergent buse. Ces flux, qu'ils soient exactement soluble ou non, peuvent souvent être soigneusement étudiée et comprise.
Turbulence
Turbulence est à la charge du temps chaotique comportement vu dans de nombreux écoulements de fluides. Il est généralement admis que ce est en raison de la l'inertie du fluide dans son ensemble: l'aboutissement de temps d'accélération dépendant et convective; De là découle où les effets inertiels sont petites ont tendance à être laminaire (le Nombre de Reynolds quantifie combien le débit est affectée par l'inertie). On croit, mais pas connu avec certitude, que les équations de Navier-Stokes modèle turbulences correctement.
Même si la turbulence est une expérience quotidienne, il est extrêmement difficile de trouver des solutions, de quantifier, ou caractérisent général. A $ 1,000,000 prix a été offert en mai 2000 par le Clay Mathematics Institute à celui qui rend progrès préliminaire vers une théorie mathématique qui aidera à la compréhension de ce phénomène.
La solution numérique des équations de Navier-Stokes pour un écoulement turbulent est extrêmement difficile, et en raison des significativement différentes échelles mélange de longueur qui sont impliqués dans l'écoulement turbulent, la solution stable de ce nécessite une telle résolution à mailles fines que le temps de calcul devient significativement impossible pour le calcul (voir Simulation numérique directe). Des tentatives pour résoudre l'écoulement turbulent en utilisant un solveur laminaire résulter typiquement dans une solution instable dans le temps, qui ne parvient pas à converger de manière appropriée. Pour contrer cela, plusieurs approximations comme la moyenne par Reynolds équations de Navier-Stokes (RANS), complétées par des modèles de turbulence (comme le modèle k-ε), sont utilisés dans la dynamique des fluides computationnelle pratiques (CFD) des applications lors de la modélisation des écoulements turbulents. Une autre technique pour résoudre numériquement l'équation de Navier-Stokes est la simulation des grandes échelles (LES). Cette approche est mathématiquement plus cher que la méthode RANS (dans le temps et la mémoire de l'ordinateur), mais produit de meilleurs résultats, puisqu'une partie des échelles caractéristiques turbulentes sont explicitement résolu.
Applicabilité
Avec équations supplémentaires (par exemple, la conservation de la masse) et des conditions aux limites bien formulées, les équations de Navier-Stokes semblent modéliser mouvement fluide avec précision; même écoulements turbulents semblent (en moyenne) d'accord avec les observations du monde réel.
Les équations de Navier-Stokes supposent que le fluide étudié est un continuum. À de très petites échelles ou dans des conditions extrêmes, fluides réels fabriqués à partir de molécules discrètes va produire des résultats différents de fluides continus modélisés par les équations de Navier-Stokes. En fonction de la Nombre de Knudsen du problème, la mécanique statistique ou peut-être même dynamique moléculaire peuvent être une approche plus appropriée.
Une autre limitation est tout simplement la nature complexe des équations. Temps formulations testées existent pour les familles de fluide commun, mais l'application des équations de Navier-Stokes aux familles moins courantes tend à conduire à des formulations très complexes qui sont un domaine de recherche en cours. Pour cette raison, les équations de Navier-Stokes sont généralement écrites pour Fluides newtoniens.
Dérivation et la description
La dérivation des équations de Navier-Stokes commence par la conservation de la masse, l'élan et l'énergie en cours d'écriture pour un volume de commande arbitraire. Dans un référentiel inertiel, la forme la plus générale des équations de Navier-Stokes finit par être:
où  est la vitesse d'écoulement,
est la vitesse d'écoulement,  est la densité du fluide, p est la pression,
est la densité du fluide, p est la pression, 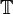 est le ( déviatorique) tenseur, et
est le ( déviatorique) tenseur, et  représente les forces du corps (par unité de volume) agissant sur le fluide et
représente les forces du corps (par unité de volume) agissant sur le fluide et  est le del opérateur. Ce est une déclaration de la conservation du moment dans un fluide et ce est une application de la deuxième loi de Newton à un continuum. Cette équation est souvent écrit en utilisant la dérivé de fond, ce qui rend plus évident que ce est une déclaration de la loi de Newton:
est le del opérateur. Ce est une déclaration de la conservation du moment dans un fluide et ce est une application de la deuxième loi de Newton à un continuum. Cette équation est souvent écrit en utilisant la dérivé de fond, ce qui rend plus évident que ce est une déclaration de la loi de Newton:
Le côté gauche de l'équation décrit l'accélération, et peut être composé d'effets dépendant du temps ou de convection (également les effets de la non-coordonnées inertielles si présents). Le côté droit de l'équation est en effet d'une sommation de les forces du corps (telles que la pesanteur) et des dérivées spatiales des forces de surface (de pression et de stress).
Accélération convective

Une caractéristique très importante des équations de Navier-Stokes est la présence de accélération convective. Ces termes désignent le temps d'accélération d'un fluide indépendant par rapport à l'espace, et sont représentés par la quantité:
Le gradient du vecteur de vitesse serait plus correctement être rédigée avec le comme tenseur dérivé de 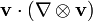 Où
Où  est le Matrice jacobienne de la vitesse par rapport à l'espace. Il ya quelques autres façons de représenter convection:
est le Matrice jacobienne de la vitesse par rapport à l'espace. Il ya quelques autres façons de représenter convection:
Le deuxième formulaire ci-dessus utilise le opérateur d'advection et est commune (noter la différence entre advection et convection - advection se réfère spécifiquement au transport d'un scalaire). La troisième forme a utiliser dans l'écoulement irrotationnel, où le boucle de la vitesse (appelé tourbillon)  est absent.
est absent.
Indépendamment de ce type de fluide est traitée, l'accélération convective est un effet non linéaire. La convection est présente dans la plupart des flux, exceptions comprennent rampante débit et incompressible dans une dimension.
Souligne
Le stress dans le fluide est représenté par la  et
et  termes, ce sont des gradients de forces de surface, analogues à des contraintes dans un solide.
termes, ce sont des gradients de forces de surface, analogues à des contraintes dans un solide.  est appelé le gradient de pression et provient de contraintes normales que l'on rencontre dans presque toutes les situations, dynamiques ou non.
est appelé le gradient de pression et provient de contraintes normales que l'on rencontre dans presque toutes les situations, dynamiques ou non.  classiquement décrit forces visqueuses; pour l'écoulement incompressible, ce ne est qu'un effet de cisaillement.
classiquement décrit forces visqueuses; pour l'écoulement incompressible, ce ne est qu'un effet de cisaillement.
Fait intéressant, que le gradient de pression présente, elle-même pas la pression. L'effet du gradient de pression, ce est que le fluide se écoule à partir de la haute pression à la basse pression.
Le terme de stress  contient trop d'inconnues pour être immédiatement utilisable, donc la forme générale ci-dessus ne est pas directement applicable à des problèmes pratiques. Pour cette raison, les hypothèses sur le comportement visqueux spécifique d'un fluide sont réalisés (basées sur des observations naturelles) et appliqués afin de préciser cette quantité en termes de variables familiers, comme la vitesse. Par exemple, ce terme devient la quantité utile
contient trop d'inconnues pour être immédiatement utilisable, donc la forme générale ci-dessus ne est pas directement applicable à des problèmes pratiques. Pour cette raison, les hypothèses sur le comportement visqueux spécifique d'un fluide sont réalisés (basées sur des observations naturelles) et appliqués afin de préciser cette quantité en termes de variables familiers, comme la vitesse. Par exemple, ce terme devient la quantité utile 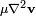 lorsque le fluide est supposé incompressible et Newtonien.
lorsque le fluide est supposé incompressible et Newtonien.
D'autres forces
 représente «autres» ( la force du corps) des forces. Généralement, ce ne est que la gravité , mais peut inclure d'autres domaines (comme électromagnétique). Dans un non inertiel système de coordonnées, d'autres «forces» telle que celle associée à coordonnées de rotation peuvent être insérés.
représente «autres» ( la force du corps) des forces. Généralement, ce ne est que la gravité , mais peut inclure d'autres domaines (comme électromagnétique). Dans un non inertiel système de coordonnées, d'autres «forces» telle que celle associée à coordonnées de rotation peuvent être insérés.
Souvent, ces forces peuvent être représentés par la pente d'une certaine quantité scalaire. La gravité de la 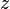 direction, par exemple, est le gradient de
direction, par exemple, est le gradient de 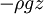 . Comme la pression ne se présente comme un gradient, ce qui implique que la résolution d'un problème sans effort corporel tel peut être réparé afin d'inclure la force de corps en modifiant la pression.
. Comme la pression ne se présente comme un gradient, ce qui implique que la résolution d'un problème sans effort corporel tel peut être réparé afin d'inclure la force de corps en modifiant la pression.
Autres équations
Les équations de Navier-Stokes sont strictement une déclaration de la conservation du moment. Afin de décrire complètement l'écoulement du fluide, plus d'informations sont nécessaires (combien dépend des hypothèses retenues), ce qui peut inclure des données de limite ( sans glissement, surface capillaire, etc.), la conservation de la masse, la conservation de l'énergie, et / ou un équation d'état.
Quelles que soient les hypothèses de flux, une déclaration de la conservation de la masse est généralement nécessaire. Ceci est réalisé à travers la masse équation de continuité, donnée dans sa forme la plus générale:
ou, en utilisant le dérivé de fond:
Ecoulement incompressible des fluides newtoniens
La grande majorité des travaux sur les équations de Navier-Stokes est fait en vertu d'un hypothèse d'écoulement incompressible Fluides newtoniens. L'hypothèse d'un fluide incompressible détient généralement bien, même lorsqu'il se agit d'un fluide "compressible", tel que l'air à la température ambiante (même lorsqu'il se écoule jusqu'à environ Mach 0,3). Prenant l'hypothèse d'écoulement incompressible en compte et en supposant viscosité constante, les équations de Navier-Stokes vont lire (sous forme vectorielle):
f représente «autres» les forces du corps (forces par unité de volume), tels que la gravité ou force centrifuge. Ce est bien la peine d'observer le sens de chaque terme:
Notez que seuls les termes convectifs sont non linéaires pour l'écoulement newtonien incompressible. L'accélération convective est une accélération provoquée par un changement (éventuellement en continu) dans la vitesse en position, par exemple l'accélération du fluide entrant dans une convergence buse. Bien que les particules de fluide individuels sont accélérés et par conséquent sont en mouvement instable, le champ d'écoulement (une distribution de vitesse) ne sera pas forcément dépendants du temps.
Une autre observation importante est que la viscosité est représenté par la vecteur de Laplace du champ de vitesse. Cela signifie que la viscosité newtonienne est la diffusion de l'impulsion, ce fonctionne de la même manière que le diffusion de la chaleur dans le voit équation de la chaleur (qui implique également le Laplacien).
Si les effets de la température sont également négligés, la seule équation «autre» (en dehors des conditions initiales / limites) nécessaire est l'équation de continuité de masse. Dans l'hypothèse incompressible, la densité est une constante et il en résulte que l'équation simplifie à:
Ce est plus précisément une déclaration de la conservation du volume (voir divergence).
Ces équations sont couramment utilisés dans les trois systèmes de coordonnées: Cartésienne, cylindrique et sphérique . Les équations cartésiennes découlent directement de l'équation de vecteur ci-dessus, l'obtention d'équations dans d'autres systèmes de coordonnées nécessitera une changement de variables.
Les coordonnées cartésiennes
Écrit l'équation vectorielle explicitement,
Notez que la gravité a été comptabilisée comme une force du corps, et les valeurs de 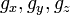 dépend de l'orientation de gravité par rapport à l'ensemble de coordonnées choisi.
dépend de l'orientation de gravité par rapport à l'ensemble de coordonnées choisi.
L'équation de continuité lit comme suit:
On notera que les composantes de la vitesse (les variables dépendantes à résoudre pour) sont 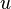 ,
, 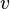 ,
, 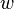 . Ce système de quatre équations comprend la forme la plus couramment utilisé et étudié. Bien que relativement plus compact que les autres représentations, ce est un système non linéaire des équations aux dérivées partielles pour lesquelles des solutions sont difficiles à obtenir.
. Ce système de quatre équations comprend la forme la plus couramment utilisé et étudié. Bien que relativement plus compact que les autres représentations, ce est un système non linéaire des équations aux dérivées partielles pour lesquelles des solutions sont difficiles à obtenir.
Coordonnées cylindriques
Un changement de variables sur les équations cartésiennes donnera les équations de quantité de mouvement suivantes pour r, θ, et z:
Les composants de gravité ne seront généralement pas constantes, mais pour la plupart des applications, soit les coordonnées sont choisis de sorte que les composantes de la gravité sont constantes, ou bien il est supposé que la gravité est compensée par un champ de pression (par exemple, le débit dans le tuyau horizontal est traitée normalement sans la gravité et sans gradient de pression vertical). L'équation de continuité est:
Cette représentation cylindrique des incompressibles équations de Navier-Stokes est le deuxième le plus souvent vu (le premier étant cartésien ci-dessus). Les coordonnées cylindriques sont choisis pour tirer parti de la symétrie, de sorte qu'une composante de vitesse peut disparaître. Un cas très commun est l'écoulement de révolution, où il n'y a pas de vitesse tangentielle (  ) Et les quantités restantes sont indépendants de
) Et les quantités restantes sont indépendants de 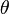 :
:
Coordonnées sphériques
En coordonnées sphériques , le  ,
, 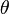 Et
Et  équations de momentum sont (noter la convention utilisée:
équations de momentum sont (noter la convention utilisée:  est colatitude):
est colatitude):
La continuité de masse va lire:
Ces équations pourraient être (légèrement) simplifié, par exemple, l'affacturage 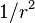 des termes visqueux. Ceci ne est pas fait pour préserver la structure du laplacien et les autres grandeurs.
des termes visqueux. Ceci ne est pas fait pour préserver la structure du laplacien et les autres grandeurs.
Flux formulation de fonction
Prendre le friser les résultats de l'équation de Navier-Stokes dans l'élimination de la pression. Cela est particulièrement facile de voir si le débit cartésienne 2D est supposé (  et aucune dépendance de rien sur
et aucune dépendance de rien sur 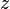 ), Où les équations se réduisent à:
), Où les équations se réduisent à:
Différencier la première par rapport à  , La seconde par rapport à
, La seconde par rapport à 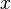 et en soustrayant les équations résultantes permettra d'éliminer toute pression et force potentielle. Définition de la fonction de courant
et en soustrayant les équations résultantes permettra d'éliminer toute pression et force potentielle. Définition de la fonction de courant 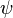 par
par
résultats dans la continuité de masse étant inconditionnellement satisfaits (étant donné la fonction est continue des cours d'eau), puis incompressible dynamique 2D newtonienne et conservation de la masse se dégradent dans une équation:
où  est le (2D) opérateur et biharmonique
est le (2D) opérateur et biharmonique 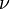 est le le viscosité cinématique. Cette équation simple avec des conditions aux limites appropriées décrit l'écoulement du fluide 2D, en prenant la viscosité cinématique seulement en tant que paramètre. On notera que l'équation pour rampante résultats de débit lorsque le côté gauche est supposé zéro.
est le le viscosité cinématique. Cette équation simple avec des conditions aux limites appropriées décrit l'écoulement du fluide 2D, en prenant la viscosité cinématique seulement en tant que paramètre. On notera que l'équation pour rampante résultats de débit lorsque le côté gauche est supposé zéro.
Écoulements compressibles des fluides newtoniens
Il ya certains phénomènes exceptionnels qui sont étroitement liés avec le fluide compressibilité. L'un des exemples évidents est sonore . Description de ces phénomènes nécessite présentation plus générale de l'équation de Navier-Stokes qui tient compte de la compressibilité du fluide. Si la viscosité est supposé un, un mandat supplémentaire constante apparaît, comme indiqué ici:
où μ v est le deuxième coefficient de viscosité. Elle est liée à viscosité de volume ou viscosité apparente. Ce terme supplémentaire disparaît pour un fluide incompressible, lorsque le divergence du flux est égal à 0.
Application à des problèmes spécifiques
Les équations de Navier-Stokes, même lorsqu'il est rédigé expressément pour les fluides spécifiques, sont plutôt de nature générique et leur bonne application à des problèmes spécifiques peuvent être très diverses. Ce est en partie parce qu'il ya une grande variété de problèmes qui peuvent être modélisés, allant d'aussi simple que la distribution de la pression statique aussi compliqué que l'écoulement polyphasique entraînée par la tension de surface .
Généralement, application à des problèmes spécifiques commence avec quelques hypothèses de flux et la formulation de condition initiale / limite, cela peut être suivi par analyse à grande échelle de simplifier encore le problème. Par exemple, après avoir assumé constante, parallèlement, une pression nonconvective dimensions entraînée flux entre les plaques parallèles, le résultant échelle (dimension) problème aux limites est:
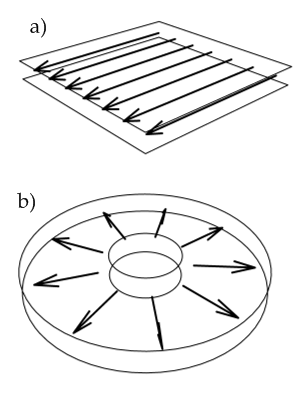
La condition limite est le aucune condition de glissement. Ce problème se résout facilement pour le champ d'écoulement:
Partir de ce point de plus grandes quantités d'intérêt peuvent être facilement obtenues, telles que la force de traînée visqueuse ou débit net.
Des difficultés peuvent survenir lorsque le problème devient un peu plus compliqué. Une torsion apparemment modeste sur le flux parallèle ci-dessus serait l'écoulement radial entre des plaques parallèles; il se agit de la convection et donc la non-linéarité. Le champ de vitesse peut être représentée par une fonction  qui doit satisfaire:
qui doit satisfaire:
Cette équation différentielle ordinaire est ce qui est obtenu lorsque les équations de Navier-Stokes sont écrites et les hypothèses de flux appliquées (en outre, le gradient de pression est résolu pour). Le terme non linéaire en fait un problème très difficile à résoudre analytiquement (une longue solution implicite peut être trouvé qui implique intégrales elliptiques et racines de polynômes cubiques). Problèmes avec l'existence réelle de solutions surgissent R> 22,609 (environ), le paramètre R étant le Nombre de Reynolds avec échelles choisies de manière appropriée. Ce est un exemple d'hypothèses de flux de perdre leur applicabilité, et un exemple de la difficulté de "haute" nombre de Reynolds se écoule.






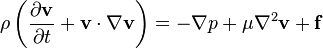

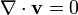


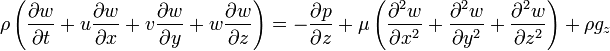

![\ Rho \ gauche (\ frac {\ U_r partielle} {\ t partielle} + U_r \ frac {\ de U_r partielle} {\ r partielle} + \ frac {u _ {\ theta}} {r} \ frac {\ U_r partielle } {\ partial \ theta} + u_z \ frac {\ U_r partielle} {\ z partielle} - \ frac {u _ {\ theta} ^ 2} {r} \ right) = - \ frac {\ p partielle} {\ r partielle} + \ mu \ left [\ frac {1} {r} \ frac {\ partial} {\ r partielle} \ left (r \ frac {\ de U_r partielle} {\ r partielle} \ right) + \ frac {1} {r ^ 2} \ frac {\ partial ^ 2 U_r} {\ partial \ theta ^ 2} + \ frac {\ de U_r partielle ^ 2} {\ z partielle ^ 2} - \ frac {U_r} {r ^ 2} - \ frac {2} {r ^ 2} \ frac {\ partial u _ {\ theta}} {\ partial \ theta} \ right] + \ rho g_r](../../images/181/18167.png)
![\ Rho \ gauche (\ frac {\ u _ {\ theta} partielle} {\ t partielle} + U_r \ frac {\ partial u _ {\ theta}} {\ r partielle} + \ frac {u _ {\ theta}} { r} \ frac {\ partial u _ {\ theta}} {\ partial \ theta} + u_z \ frac {\ partial u _ {\ theta}} {\ z partielle} + \ frac {U_r u _ {\ theta}} {r } \ right) = - \ frac {1} {r} \ frac {\ p partielle} {\ partial \ theta} + \ mu \ left [\ frac {1} {r} \ frac {\ partial} {\ partial r} \ left (r \ frac {\ partial u _ {\ theta}} {\ r partielle} \ right) + \ frac {1} {r ^ 2} \ frac {\ partial ^ 2 u _ {\ theta}} { \ partial \ theta ^ 2} + \ frac {\ partial ^ 2 u _ {\ theta}} {\ partial z ^ 2} + \ frac {2} {r ^ 2} \ frac {\ U_r partielle} {\ partial \ theta} - \ frac {u _ {\ theta}} {r ^ 2} \ right] + \ rho g _ {\ theta}](../../images/181/18168.png)
![\ Rho \ gauche (\ frac {\ u_z partielle} {\ t partielle} + U_r \ frac {\ de u_z partielle} {\ r partielle} + \ frac {u _ {\ theta}} {r} \ frac {\ u_z partielle } {\ partial \ theta} + u_z \ frac {\ u_z partielle} {\ z partielle} \ right) = - \ frac {\ p partielle} {\ z partielle} + \ mu \ left [\ frac {1} { r} \ frac {\ partial} {\ r partielle} \ left (r \ frac {\ u_z partielle} {\ r partielle} \ right) + \ frac {1} {r ^ 2} \ frac {\ partial ^ 2 u_z} {\ partial \ theta ^ 2} + \ frac {\ partial ^ 2 u_z} {\ z partielle ^ 2} \ right] + \ rho g_z](../../images/181/18169.png)

![\ Rho \ gauche (\ frac {\ U_r partielle} {\ t partielle} + U_r \ frac {\ de U_r partielle} {\ r partielle} + u_z \ frac {\ U_r partielle} {\ z partielle} \ right) = - \ frac {\ p partielle} {\ r partielle} + \ mu \ left [\ frac {1} {r} \ frac {\ partial} {\ r partielle} \ left (r \ frac {\ U_r partielle} {\ r partielle} \ right) + \ frac {\ partial ^ 2 U_r} {\ partial z ^ 2} - \ frac {} {U_r r ^ 2} \ right] + \ rho g_r](../../images/181/18172.png)
![\ Rho \ gauche (\ frac {\ u_z partielle} {\ t partielle} + U_r \ frac {\ de u_z partielle} {\ r partielle} + u_z \ frac {\ u_z partielle} {\ z partielle} \ right) = - \ frac {\ p partielle} {\ z partielle} + \ mu \ left [\ frac {1} {r} \ frac {\ partial} {\ r partielle} \ left (r \ frac {\ u_z partielle} {\ r partielle} \ right) + \ frac {\ partial ^ 2 u_z} {\ z partielle ^ 2} \ right] + \ rho g_z](../../images/181/18173.png)


![\ Mu \ left [\ frac {1} {r ^ 2} \ frac {\ partial} {\ r partielle} \ left (r ^ 2 \ frac {\ de U_r partielle} {\ r partielle} \ right) + \ frac {1} {r ^ 2 \ sin (\ phi) ^ 2} \ frac {\ partial ^ 2 U_r} {\ partial \ theta ^ 2} + \ frac {1} {r ^ 2 \ sin (\ phi)} \ frac {\ partial} {\ partial \ phi} \ left (\ sin (\ phi) \ frac {\ U_r partielle} {\ partial \ phi} \ right) - 2 \ frac {U_r + \ frac {\ u_ partielle {\ phi}} {\ partial \ phi} + u _ {\ phi} \ lit bébé (\ phi)} {r ^ 2} + \ frac {2} {r ^ 2 \ sin (\ phi)} \ frac {\ partielle u _ {\ theta}} {\ partial \ theta} \ right]](../../images/181/18176.png)
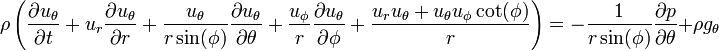
![\ Mu \ left [\ frac {1} {r ^ 2} \ frac {\ partial} {\ r partielle} \ left (r ^ 2 \ frac {\ partial u _ {\ theta}} {\ r partielle} \ right ) + \ frac {1} {r ^ 2 \ sin (\ phi) ^ 2} \ frac {\ partial ^ 2 u _ {\ theta}} {\ partial \ theta ^ 2} + \ frac {1} {r ^ 2 \ sin (\ phi)} \ frac {\ partial} {\ partial \ phi} \ left (\ sin (\ phi) \ frac {\ partial u _ {\ theta}} {\ partial \ phi} \ right) + \ frac {2 \ frac {\ U_r partielle} {\ partial \ theta} + 2 \ cos (\ phi) \ frac {\ partial u _ {\ theta}} {\ partial \ theta} - u _ {\ theta}} { r ^ 2 \ sin (\ phi) ^ 2} \ right]](../../images/181/18178.png)

![\ Mu \ left [\ frac {1} {r ^ 2} \ frac {\ partial} {\ r partielle} \ left (r ^ 2 \ frac {\ partial u _ {\ phi}} {\ r partielle} \ right ) + \ frac {1} {r ^ 2 \ sin (\ phi) ^ 2} \ frac {\ partial ^ 2 u _ {\ phi}} {\ partial \ theta ^ 2} + \ frac {1} {r ^ 2 \ sin (\ phi)} \ frac {\ partial} {\ partial \ phi} \ left (\ sin (\ phi) \ frac {\ partial u _ {\ phi}} {\ partial \ phi} \ right) + \ frac {2} {r ^ 2} \ frac {\ U_r partielle} {\ \ partielle phi} - \ frac {u _ {\ phi} + 2 \ cos (\ phi) \ frac {\ partial u _ {\ theta} } {\ partial \ theta}} {r ^ 2 \ sin (\ phi) ^ 2} \ right]](../../images/181/18180.png)