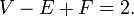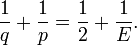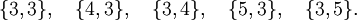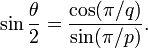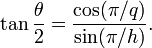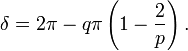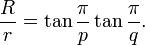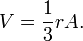Solide de Platon

Saviez-vous ...

Cette sélection écoles a été choisi par SOS Enfants pour les écoles dans le monde en développement ne ont pas accès à Internet. Il est disponible en téléchargement intranet. Cliquez ici pour en savoir plus sur le parrainage d'enfants.

«Solide platonicien» est un convexe polyèdre régulier. Ce sont les analogues en trois dimensions de la partie convexe polygones réguliers. Il ya exactement cinq de ces chiffres (ci-dessous). Ils sont uniques en ce que les faces, les arêtes et les angles sont tous congruents.

Polyèdres réguliers Cinq Convex (des solides de Platon)
Tétraèdre	Hexaèdre ou Cube	Octaèdre	Dodécaèdre	Icosaèdre
( animation )	( animation )	( animation )	( Animation)	( animation )

Le nom de chaque figure est dérivé du nombre de ses faces respectivement: 4, 6, 8, 12 et 20.

Le la beauté esthétique et la symétrie des solides de Platon en ont fait un sujet de prédilection des géomètres pour des milliers d'années. Ils sont nommés pour le philosophe grec Platon qui a théorisé la éléments classiques ont été construits à partir des solides réguliers.

Histoire

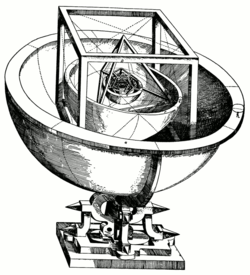
Modèle solide platonicien de Kepler du système solaire à partir de Mysterium Cosmographicum (1596)

Les solides de Platon ont été connus depuis l'antiquité. Modèles ornés d'entre eux peuvent être trouvés parmi les boules de pierre sculptés créées par la fin les gens néolithiques de l'Ecosse au moins 1000 ans avant Platon (Atiyah et Sutcliffe 2003).

Les anciens Grecs ont étudié les solides de Platon abondamment. Certaines sources (telles que Proclus) crédit Pythagore avec leur découverte. D'autres données indiquent qu'il pourrait avoir été seulement familier avec le tétraèdre, le cube, et le dodécaèdre, et que la découverte de l'octaèdre et l'icosaèdre appartiennent à Théétète, un contemporain de Platon. Dans tous les cas, Théétète a donné une description mathématique de tous les cinq ans et peut avoir été responsable de la première preuve connue qu'il n'y a pas d'autres polyèdres réguliers convexes.

Les solides de Platon figurent en bonne place dans la philosophie de Platon pour qui ils sont nommés. Platon a écrit à leur sujet dans le dialogue Timée c 0,360 BC dans laquelle il associé chacun des quatre éléments classiques ( terre, l'air, l'eau, et feu) avec un solide régulier. Terre a été associée avec le cube, l'octaèdre avec l'air, l'eau avec l'icosaèdre, et le feu avec le tétraèdre. Il y avait justification intuitive de ces associations: la chaleur du feu se sent forte et poignardant (comme la petite tétraèdres). L'air est constitué de l'octaèdre; ses composants minuscules sont si lisse que l'on peut à peine sentir. L'eau, l'icosaèdre, se écoule de l'un de la main quand ramassé, comme si elle est faite de minuscules petites boules. En revanche, un solide hautement non sphérique, l'hexaèdre (cube) représente la terre. Ces petits solides maladroits provoquent la saleté à se effriter et de briser quand ramassé, en nette différence au bon écoulement de l'eau. Le cinquième platonicienne solide, le dodécaèdre, Platon remarques obscurément, "... le dieu utilisé pour organiser les constellations sur le ciel tout entier". Aristote ajouté un cinquième élément, Aither (éther en latin, "éther" en anglais) et postulé que les cieux ont été faits de cet élément, mais il ne avait aucun intérêt à faire correspondre avec Platon cinquième solide.

Euclide a donné une description mathématique complète des solides de Platon dans les éléments ; le dernier livre (Livre XIII) qui est consacrée à leurs propriétés. Propositions 13-17 dans le Livre XIII décrivent la construction du tétraèdre, l'octaèdre, cube, icosaèdre et dodécaèdre dans cet ordre. Pour chaque solide Euclide trouve le rapport du diamètre de la sphère circonscrite à la longueur d'arête. Dans la proposition 18, il fait valoir qu'il n'y a pas encore polyèdres réguliers convexes. Une grande partie de l'information dans le Livre XIII est probablement dérivé du travail du Théétète.

Dans le 16ème siècle , le Allemand astronome Johannes Kepler a tenté de trouver une relation entre les cinq connus planètes à l'époque (à l'exclusion de la Terre) et les cinq solides de Platon. En Mysterium Cosmographicum, publié en 1596, Kepler établi un modèle du système solaire dans lequel les cinq solides ont été mis à l'intérieur de l'autre et séparées par une série de sphères inscrites et circonscrites. Les six sphères chaque correspondaient à l'une des planètes ( Mercure , Vénus , la Terre , Mars , Jupiter et Saturne ). Les solides ont été commandés avec la plus à l'intérieur étant l'octaèdre, suivie de l'icosaèdre, dodécaèdre, tétraèdre, et enfin le cube. De cette façon, la structure du système solaire et les relations à distance entre les planètes a été dicté par les solides de Platon. En fin de compte, l'idée originale de Kepler a dû être abandonnée, mais de sa recherche a été la découverte de la Kepler solides, la réalisation que les orbites des planètes ne sont pas des cercles et des Lois de Kepler pour lequel il est désormais célèbre.

Propriétés combinatoires

Un polyèdre convexe est un solide platonique si et seulement si

toutes ses faces sont convexe congruent polygones réguliers,
aucun de ses faces se coupent à l'exception de leurs bords, et
le même nombre de faces répondre à chacune de ses sommets.

Chaque boîte solide platonicien donc être désigné par un symbole {p, q} où

p = le nombre de côtés de chaque face (ou le nombre de sommets de chaque face) et

q = le nombre de faces répondant à chaque sommet (ou le nombre de réunion des bords à chaque sommet).

Le symbole {p, q}, appelé Symbole Schläfli, donne une combinatoire Description du polyèdre. Les symboles Schläfli des cinq solides de Platon sont donnés dans le tableau ci-dessous.

Polyèdre	Sommets	Bords	Visages	Symbole Schläfli	Sommet configuration
tétraèdre	4	6	4	{3, 3}	3.3.3
cube	8	12	6	{4, 3}	4.4.4
octaèdre	6	12	8	{3, 4}	3.3.3.3
dodécaèdre	20	30	12	{5, 3}	5.5.5
icosaèdre	12	30	20	{3, 5}	3.3.3.3.3

Toutes les autres informations combinatoire de ces solides, tels que le nombre total de sommets (V), les bords (E), et des faces (F), peut être déterminée à partir de p et q. Depuis ne importe quel bord se joint deux sommets et a deux faces adjacentes nous devons avoir:

$pF = 2E = qV. \,$

L'autre relation entre ces valeurs est donnée par la formule d'Euler :

$V - E + F = 2. \,$

Ce fait peut être prouvé non triviale dans une grande variété de moyens (en topologie algébrique il résulte du fait que la caractéristique d'Euler de la sphère est de 2). L'ensemble de ces trois relations déterminent complètement V, E et F:

$V = \ frac {} {4p 4 - (P-2) (q-2)}, \ quad E = \ frac {} {2pq 4 - (P-2) (q-2)}, \ quad F = \ frac {} {4 4q - (P-2) (q-2)}.$

Notez que la permutation p et q échanges F et V tout en laissant inchangée E (Pour une interprétation géométrique de ce fait, voir la section sur la double polyèdres ci-dessous).

Classification

Ce est un résultat classique qu'il n'y a que cinq polyèdres réguliers convexes. Deux arguments communs sont donnés ci-dessous. Ces deux arguments ne montrent qu'il peut y avoir pas plus de cinq solides de Platon. Que les cinq existe réellement, ce est une question-une séparé qui peut être répondu par une construction explicite.

Preuve géométrique

L'argument géométrique suivante est très similaire à celle donnée par Euclide dans les Éléments:

Chaque sommet du solide doit coïncider avec un sommet de chacun d'au moins trois faces.
A chaque sommet du solide, le total, entre les faces adjacentes, des angles entre les côtés adjacents respectifs doit être inférieure à 360 °.
Les angles à tous les sommets de toutes les faces d'un solide platonicien sont identiques, de sorte que chaque sommet de chaque face doivent contribuer à moins de 360 ° / 3 = 120 °.
Polygones réguliers de six ou plusieurs parties ont que des angles de 120 ° ou plus, de sorte que la face commune doit être le triangle, carré, ou d'un pentagone. Et pour:
- Triangulaires visages: chaque sommet d'un triangle régulier est de 60 °, donc une forme peut avoir trois, quatre ou cinq triangles réunis à un sommet; ceux-ci sont respectivement le tétraèdre, l'octaèdre, et l'icosaèdre.
- Place face: chaque sommet d'un carré est de 90 °, il n'y a donc qu'un seul arrangement possible avec trois visages à un sommet, le cube.
- Pentagonale face: chaque sommet est de 108 °; de plus, seulement un agencement, de trois faces à un sommet est possible, le dodécaèdre.

La preuve topologique

Un purement topologique preuve peut être faite en utilisant seulement des informations combinatoire sur les solides. La clé est l'observation d'Euler que $V - E + F = 2$ Et le fait que $pF = 2E = qV$ . La combinaison de ces équations on obtient l'équation

$\ Frac {} {2E q} - E + \ frac {} {2E p} = 2.$

Manipulation algébrique simple donne alors

${1 \ over q} + {1 \ over p} = {1 \ over 2} + {1 \ over E}.$

Depuis $E$ est strictement positif, nous devons avoir

$\ Frac {1} {q} + \ frac {1} {p}> \ frac {1} {2}.$

En utilisant le fait que p et q doivent tous deux être d'au moins 3, on peut facilement voir qu'il n'y a que cinq possibilités pour {p, q}:

$\ {3, 3 \}, \ quad \ {4, 3 \}, \ quad \ {3, 4 \}, \ quad \ {5, 3 \}, \ quad \ {3,5 \}.$

Propriétés géométriques

Angles

Il ya un certain nombre d' angles associés à chaque solide platonicien. Le dièdre est l'angle intérieur entre deux plans tout le visage. L'angle dièdre θ, du solide {p, q} est donnée par la formule

$\ Péché {\ theta \ over 2} = \ frac {\ cos (\ pi / q)} {\ sin (\ pi / p)}.$

Ceci est parfois plus commodément exprimée en termes de la tangente par:

$\ Tan {\ theta \ over 2} = \ frac {\ cos (\ pi / q)} {\ sin (\ pi / h)}.$

La quantité h est 4, 6, 6, 10, et 10 pour le tétraèdre, le cube, l'octaèdre, le dodécaèdre, et l'icosaèdre respectivement.

Le carence angulaire au niveau du sommet d'un polyèdre est la différence entre la somme des angles au visage que sommet et 2π. Le défaut, δ, à ne importe quel sommet des solides platoniciens {p, q} est

$\ Delta = 2 \ pi - q \ pi \ gauche (1- {2 \ over p} \ right).$

Par Théorème de Descartes, ce est égal à 4π divisé par le nombre de sommets (ce est à dire la défaillance totale à tous les sommets est 4π).

Analogue trois dimensions d'un angle plan est un angle solide. L'angle solide, Ω, au sommet d'un solide platonicien est donnée en termes de l'angle dièdre par

$\ Omega = q \ theta -. (Q-2) \ pi \,$

Cela découle de la formule excès sphérique pour un polygone sphérique et le fait que le Figure de sommet du polyèdre {p, q} est un q -gon régulière.

Les différents angles associés avec les solides de Platon sont rassemblés ci-dessous. Les valeurs numériques des angles solides sont donnés dans stéradians. La constante φ = (1 + √5) / 2 est le nombre d'or .

Polyèdre	Dièdre 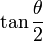$(\ Theta) \,$	$\ Tan \ frac {\ theta} {2}$	Défaut $(\ Delta) \,$	Angle solide $(\ Omega) \,$
tétraèdre	70,53 °	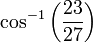$1 \ over {\ sqrt 2}$	$\ Pi \,$	$\ Cos ^ {- 1} \ left (\ frac {23} {27} \ right)$	$\ Environ 0.551286$
cube	90 °	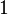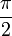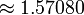$1 \,$	$\ Pi \ over 2$	$\ Frac {\ pi} {2}$	$\ Environ 1,57080$
octaèdre	109,47 °	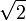$\ Sqrt 2$	${2 \ pi} \ plus de 3$	$4 \ sin ^ {- 1} \ left ({1 \ over 3} \ right)$	$\ Environ 1,35935$
dodécaèdre	116,57 °	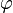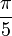$\ Varphi \,$	$\ Pi \ plus de 5$	$\ Pi - \ tan ^ {- 1} \ left (\ frac {2} {11} \ right)$	$\ Environ 2,96174$
icosaèdre	138,19 °	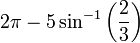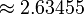$\ Varphi ^ 2 \,$	$\ Pi \ plus de 3$	$2 \ pi - 5 \ sin ^ {- 1} \ left ({2 \ plus de 3} \ right)$	$\ Environ 2,63455$

Rayons, la surface et le volume

Une autre vertu de régularité est que les solides de Platon possèdent tous trois sphères concentriques:

la sphère circonscrite qui passe à travers tous les sommets,
la midsphere qui est tangent à chaque arête au milieu de la bordure, et
la sphère inscrite qui est tangent à chaque face au centre de la face.

Le rayons de ces sphères sont appelés les circonscrit, le midradius et le inradius. Ce sont les distances du centre du polyèdre aux sommets, les milieux des bords, et des centres de visage respectivement. Le circonscrit R et r de la inradius du solide {p, q} avec une longueur d'arête sont donnés par

$R = \ left ({a \ over 2} \ right) \ tan \ frac {\ pi} {q} \ tan \ frac {\ theta} {2}$

$r = \ left ({a \ over 2} \ right) \ lit \ frac {\ pi} {p} \ tan \ frac {\ theta} {2}$

où θ est l'angle dièdre. La ρ de midradius est donnée par

$\ Rho = \ left ({a \ over 2} \ right) \ frac {\ cos (\ pi / p)} {\ sin (\ pi / h)}$

où h est la quantité utilisée ci-dessus dans la définition de l'angle dièdre (h = 4, 6, 6, 10, ou 10). A noter que le rapport entre le cercle circonscrit à la inradius est symétrique en p et q:

${R \ over r} = \ tan \ frac {\ pi} tan \ frac {\ pi} {p} \ {q}.$

Le surface, A, d'un solide platonicien {p, q} est facilement calculé comme zone d'un réguliers fois p -gon le nombre de faces F. C'est:

$A = \ left ({a \ over 2} \ right) ^ 2 Fp \ lit \ frac {\ pi} {p}.$

Le volumique est calculé comme F fois le volume de la pyramide dont la base est un p -gon régulière et dont la hauteur est la inradius r. C'est,

$V = {1 \ over 3} rA.$

Le tableau suivant répertorie les différents rayons des solides de Platon avec leur surface et le volume. La taille globale est fixé en prenant la longueur d'arête, une, pour être égal à 2.

Polyèdre (A = 2)	Inradius (r)	Midradius (ρ)	Circonscrit (R)	Surface (A)	Volume (V)
tétraèdre	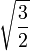$1 \ over {\ sqrt 6}$	$1 \ over {\ sqrt 2}$	$\ Sqrt {3 \ over 2}$	$4 \ sqrt 3$	$\ Frac {2 \ sqrt 2} {3}$
cube	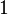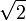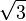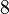$1 \,$	$\ Sqrt 2$	$\ Sqrt 3$	$24 \,$	$8 \,$
octaèdre	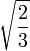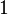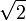$\ Sqrt {2 \ plus de 3}$	$1 \,$	$\ Sqrt 2$	$8 \ sqrt 3$	$\ Frac {8 \ sqrt 2} {3}$
dodécaèdre	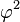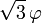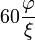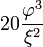$\ Frac {\ varphi ^ 2} {\ xi}$	$\ Varphi ^ 2$	$\ Sqrt 3 \, \ varphi$	$60 \ frac {\ varphi} {\ xi}$	$20 \ frac {\ varphi ^ 3} {\ xi ^ 2}$
icosaèdre	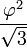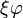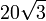$\ Frac {\ varphi ^ 2} {\ sqrt 3}$	$\ Varphi$	$\ Xi \ varphi$	$20 \ sqrt 3$	$\ Frac {20 \ varphi ^ 2} {3}$

Les constantes φ et ξ dans le ci-dessus sont donnés par

$\ Varphi = 2 \ cos {\ pi \ plus de 5} = \ frac {1+ \ sqrt 5} {2} \ qquad \ xi = 2 \ péché {\ pi \ plus de 5} = \ sqrt {\ frac {5- \ sqrt 5} {2}} = 5 ^ {1/4} \ varphi ^ {- 1/2}.$

Parmi les solides de Platon, soit le dodécaèdre ou icosaèdre peut être considérée comme la meilleure approximation de la sphère. L'icosaèdre a le plus grand nombre de visages, le plus grand angle dièdre, et il étreint sa sphère inscrite le plus serré. Le dodécaèdre, d'autre part, a le défaut angulaire plus petit, le plus grand angle solide sommet, et elle remplit sa sphère circonscrite au plus.

Symétrie

Double polyèdres

Un cube-octaèdre dual.

Chaque polyèdre a une polyèdre dual avec des visages et des sommets échangés. Le double de chaque Solide de Platon est un autre solide platonicien, de sorte que nous pouvons organiser les cinq solides dans deux paires.

Le tétraèdre est auto-double (ce est à dire son double est un autre tétraèdre).
Le cube et l'octaèdre forment une paire duale.
Le dodécaèdre et icosaèdre forment une paire duale.

Si un polyèdre a symbole Schläfli {p, q}, puis son double a le symbole {q, p}. En effet chaque propriété combinatoire d'un platonicien solide peut être interprété comme une autre propriété combinatoire de la double.

On peut construire le double polyèdre en prenant les sommets de la double comme les centres des faces de la figure originale. Les bords de la double liaison sont formés par les centres des faces adjacentes à l'original. De cette manière, le nombre de faces et de sommets est interchangé, tandis que le nombre d'arêtes reste le même.

Plus généralement, on peut dualize un solide platonique par rapport à une sphère de rayon d concentrique avec le solide. Les rayons (R, ρ, r) d'un solide et ceux de son double (R *, ρ *, r *) sont liés par

$d ^ 2 = R ^ \ ast r = r ^ \ ast R = \ rho ^ \ ast \ rho.$

Il est souvent commode de dualize par rapport à la midsphere (d = ρ) puisqu'il a la même relation avec les deux polyèdres. Prenant d ² = Rr donne un double solide avec le même circonscrit et inradius (c.-à-R * = R et r * = r).

groupes de symétrie

En mathématiques, le concept de symétrie est étudié avec la notion de groupe mathématique . Chaque polyèdre associé a un groupe de symétrie, qui est l'ensemble de toutes les transformations ( Isométries euclidiennes) qui laissent l'invariant de polyèdre. Le commande du groupe de symétrie est le nombre de symétries du polyèdre. On distingue souvent entre le groupe de symétrie complète, qui comprend réflexions, et le groupe de symétrie appropriée, qui comprend uniquement rotations.

Les groupes de symétrie des solides de Platon sont connus comme groupes polyédriques (qui sont une classe spéciale de la groupes de points en trois dimensions). Le haut degré de symétrie des solides de Platon peut être interprété de plusieurs façons. Plus important encore, les sommets de chaque solide sont tous équivalents dans le cadre du action du groupe de symétrie, de même que les arêtes et les faces. On dit de l'action du groupe de symétrie est transitive sur les sommets, arêtes et faces. En fait, ce est une autre façon de définir la régularité d'un polyèdre: un polyèdre est régulier si et seulement si elle est vertex uniforme, bord uniforme et faire face uniforme.

Il ya seulement trois groupes de symétrie associés avec les solides de Platon plutôt que cinq, puisque le groupe de symétrie de tout polyèdre coïncide avec celle de son double. Ce est facile de voir en examinant la construction de la double polyèdre. Toute la symétrie de l'original doit être une symétrie de la double et vice-versa. Les trois groupes polyédriques sont:

la tétraédrique groupe T,
la octaédrique groupe O (qui est également le groupe de symétrie du cube), et
la icosaédrique groupe I (qui est aussi le groupe de symétrie du dodécaèdre).

Les ordres des (rotation) des groupes appropriés sont 12, 24 et 60 respectivement - précisément deux fois le nombre d'arêtes dans les polyèdres respective. Les ordres des groupes de symétrie complets sont deux fois plus nouveau (24, 48 et 120). Voir (Coxeter 1973) pour une dérivation de ces faits.

Le tableau suivant présente les diverses propriétés de symétrie des solides de Platon. Les groupes de symétrie indiqués sont les groupes complets avec les sous-groupes de rotation donnée entre parenthèses (de même pour le nombre de symétries). La construction de kaléidoscope de Wythoff est un procédé pour construire des polyèdres directement à partir de leurs groupes de symétrie. Nous listons pour le symbole de référence Wythoff pour chacun des solides de Platon.

Polyèdre	Symbole Schläfli	Symbole de Wythoff	Polyèdre dual	Symétries	Groupe Symétrie
tétraèdre	{3, 3}	3 \| 2 3	tétraèdre	24 (12)	T _d (T)
cube	{4, 3}	3 \| 2 4	octaèdre	48 (24)	O _h (O)
octaèdre	{3, 4}	4 \| 2 3	cube	48 (24)	O _h (O)
dodécaèdre	{5, 3}	3 \| 2 5	icosaèdre	120 (60)	_I H (I)
icosaèdre	{3, 5}	5 \| 2 3	dodécaèdre	120 (60)	_I H (I)

Dans la nature et de la technologie

Le tétraèdre, le cube, l'octaèdre et tous se produisent naturellement dans structures cristallines. Ce ne épuisent nullement le nombre de formes possibles de cristaux. Toutefois, ni le icosaèdre régulier ni le dodécaèdre régulier sont parmi eux. L'une des formes, appelé le pyritohedron (nommé pour le groupe de minéraux dont il est typique) a douze faces pentagonales, disposé dans le même schéma que les faces du dodécaèdre régulier. Les faces de la pyritohedron sont cependant pas régulier, de sorte que le pyritohedron est également pas régulière.

Circogonia icosaèdres, une espèce de Radiolaires, la forme d'un icosaèdre régulier.

Au début du 20e siècle, Ernst Haeckel décrit (Haeckel, 1904) un certain nombre d'espèces de Radiolaires, dont certains sont en forme de squelettes différents polyèdres réguliers. Les exemples incluent Circoporus octahedrus, Circogonia icosaèdres, Lithocubus geometricus et Circorrhegma dodécaèdres. Les formes de ces animaux devraient être évidents à partir de leurs noms.

De nombreux virus , tels que le virus de l'herpès, ont la forme d'un icosaèdre régulier. Structures virales sont construites répétées identiques protéines sous-unités et l'icosaèdre est la forme la plus facile à assembler en utilisant ces sous-unités. Un polyèdre régulier est utilisé car il peut être construit à partir d'une seule unité de protéine de base utilisé encore et encore; ce qui économise de l'espace dans le virale génome.

Dans la météorologie et la climatologie, des modèles numériques mondiaux de flux atmosphérique sont d'un intérêt croissant qui utilisent des grilles qui sont basés sur un icosaèdre (affinés par triangulation) au lieu de la plus couramment utilisée longitude / latitude grille. Ceci présente l'avantage de la résolution spatiale sans uniformément répartie singularités (à savoir la pôles) au détriment d'un peu plus grande difficulté numérique.

Géométrie de cadres de l'espace est souvent basée sur des solides platoniques. Dans le système MERO, solides platoniciens sont utilisés pour la convention de dénomination des différentes configurations de châssis de l'espace. Par exemple ½ O + T fait référence à une configuration en une moitié d'un tétraèdre et octaèdre.

Solides platoniciens sont souvent utilisés pour faire dés , parce dés de ces formes peuvent être faites juste. Dés à 6 faces sont très fréquents, mais les autres numéros sont couramment utilisés dans jeux de rôle. De telles matrices sont couramment désignés sous le nom d n où n est le nombre de faces (d8, d20, etc.); voir notation dés pour plus de détails.

Dés polyédriques sont souvent utilisés dans jeux de rôle.

Ces formes montrent fréquemment dans d'autres jeux ou des puzzles. Puzzles similaires à un cube de Rubik venir dans les cinq formes - voir polyèdres magie.

Polyèdres et polytopes connexes

Polyèdres uniformes

Il existe quatre polyèdres réguliers qui ne sont pas convexe, appelé Polyèdres Kepler-Poinsot. Celles-ci ont toutes symétrie icosaédrique et peut être obtenu en tant que stellations du dodécaèdre et l'icosaèdre.

cuboctaèdre

icosidodécaèdre

La prochaine polyèdres convexes plus régulier après les solides de Platon sont les cuboctaèdre, qui est un rectification du cube et l'octaèdre, et la icosidodécaèdre, qui est une rectification du dodécaèdre et l'icosaèdre (la rectification du tétraèdre auto-dual est un octaèdre régulier). Ce sont à la fois sens quasi-régulière qu'ils sont Vertex- et le bord uniforme et ont des visages réguliers, mais les visages ne sont pas congruents (à venir dans deux classes différentes). Ils forment deux des treize Solides d'Archimède, qui sont convexes polyèdres uniformes à symétrie polyédrique.

Le polyèdres uniformes forment une classe beaucoup plus large de polyèdres. Ces chiffres sont sommet uniforme et avoir un ou plusieurs types de régulière ou polygones étoiles pour les visages. Il se agit notamment tous les polyèdres mentionné ci-dessus avec un ensemble infini de prismes, un ensemble infini de antiprismes, et 53 d'autres formes non convexe.

Le Solides de Johnson sont des polyèdres convexes qui ont visages réguliers, mais ne sont pas uniformes.

Tessellations

L'arbre pavages réguliers du plan sont étroitement liés aux solides de Platon. En effet, on peut voir les solides de Platon que les cinq mosaïques régulières de la sphère . Cela se fait en projetant chaque solide sur une sphère concentrique. Les visages projettent sur régulière polygones sphériques qui couvrent exactement la sphère. On peut montrer que chaque tessellation régulière de la sphère est caractérisé par une paire d'entiers {p, q} avec 1 / p + 1 / q> 1/2. De même, un pavage régulier du plan se caractérise la condition 1 / + 1 p / q = 1/2. Il ya trois possibilités:

{4, 4} dont une carrelage carré,
{3, 6} qui est un pavage triangulaire, et
{6, 3} qui est un pavage hexagonal (dual du carrelage triangulaire).

D'une manière similaire, on peut considérer pavages réguliers de la plan hyperbolique. Ils sont caractérisés la condition 1 / p + 1 / q <1/2. Il ya un nombre infini de ces mosaïques.

Dimensions supérieures

En plus de trois dimensions, polyèdres à généraliser polytopes, avec convexe de dimension supérieure polytopes réguliers étant les équivalents des solides de Platon en trois dimensions.

Dans le milieu du 19e siècle, le mathématicien suisse Ludwig Schläfli découvert les analogues à quatre dimensions des solides platoniciens, appelé 4-polytopes réguliers convexes. Il ya exactement six de ces chiffres; cinq sont analogues aux solides de Platon, tandis que le sixième, le 24 cellules, n'a pas d'analogue inférieure dimensions.

Dans toutes les dimensions supérieur à quatre, il ya seulement trois polytopes réguliers convexes: le simplex, le hypercube, et de la Hyperoctaèdre. En trois dimensions, celles-ci coïncident avec le tétraèdre, le cube, l'octaèdre et.

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Platonic_solid&oldid=198915089 "

Privacy Policy and Contacts (IT)