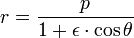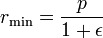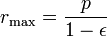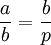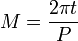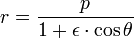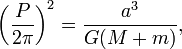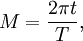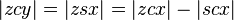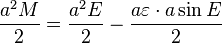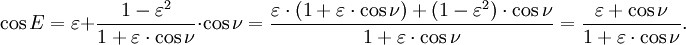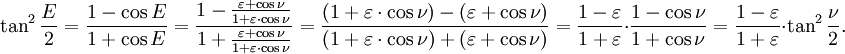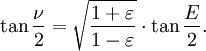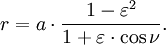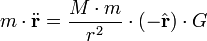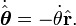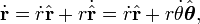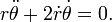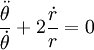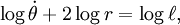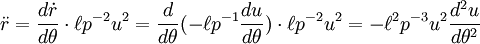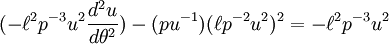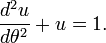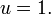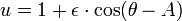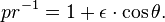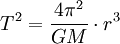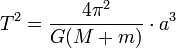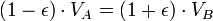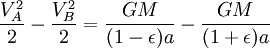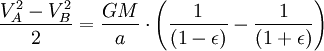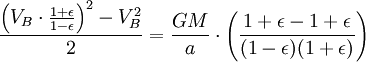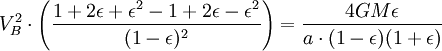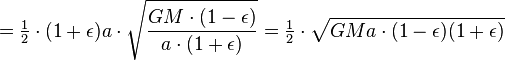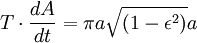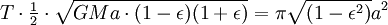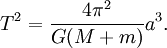Lois de Kepler

Renseignements généraux

Enfants SOS offrent un chargement complet de la sélection pour les écoles pour une utilisation sur les intranets des écoles. Cliquez ici pour en savoir plus sur le parrainage d'enfants.

Illustration de trois lois de Kepler avec deux orbites planétaires. (1) Les orbites sont des ellipses, avec les points focaux f1 et f2 pour la première planète et F1 et F3 pour la deuxième planète. Le soleil est placé dans le point focal f1. (2) Les deux secteurs ombragés A1 et A2 ont la même surface et le temps pour la planète une pour couvrir le segment A1 est égale à la durée pour couvrir le segment A2. 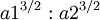(3) Les durées totales de l'orbite de la planète et une planète deux ont un rapport $a1 ^ {3/2}: a2 ^ {3/2}$ .

En astronomie , les lois de Kepler sur le mouvement planétaire sont trois lois mathématiques qui décrivent le mouvement des planètes dans le système solaire . Allemand mathématicien et astronome Johannes Kepler ( 1571- 1630) entre eux ont découvert.

Kepler a étudié la observations de l'astronome danois précise légendaire Tycho Brahe. Autour de 1605, Kepler a constaté que les observations de Brahe des positions des planètes suivaient trois lois mathématiques relativement simples.

Les lois de Kepler contestées astronomie et la physique aristotélicienne et ptolémaïque. Son affirmation selon laquelle la Terre tournait, son utilisation de ellipses plutôt que épicycles, et sa preuve que les vitesses des planètes variées, changé l'astronomie et de la physique . Néanmoins, l'explication physique du comportement des planètes est venu près d'un siècle plus tard, quand Isaac Newton était en mesure de déduire les lois de Kepler à partir de Newton propres lois du mouvement et son la loi de la gravitation universelle, en utilisant son invention du calcul . Autres modèles de la gravitation donneraient empiriquement faux résultats.

Trois lois de Kepler sont:

Le orbite de chaque planète est une ellipse avec le soleil à l'un des foyers. Une ellipse est caractérisé par ses deux points focaux; voir l'illustration. Ainsi, Kepler a rejeté l'ancienne aristotélicienne, ptolémaïque, et la croyance copernicienne dans un mouvement circulaire.
Une ligne joignant une planète et le soleil balaie des aires égales pendant des intervalles de temps égaux que la planète se déplace le long de son orbite. Cela signifie que la planète se déplace plus rapidement tout près du soleil et ralentit quand il est loin du soleil. Avec sa loi, Kepler détruit la théorie astronomique aristotélicienne que les planètes ont uniforme vitesse .
Le places de la périodes orbitales des planètes sont directement proportionnelle à la cubes de la demi-grands axes (le «demi-longueur" de l'ellipse) de leurs orbites. Cela signifie non seulement que les grandes orbites ont de plus longues périodes, mais aussi que la vitesse d'une planète sur une orbite plus grande est plus faible que dans une orbite plus petite.

Les lois de Kepler sont formulées ci-dessous, et sont établis à partir des lois de Newton, en utilisant héliocentriques coordonnées polaires 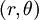$\ (R, \ theta)$ . Cependant, les lois de Kepler peuvent également être formulées et calculées à l'aide des coordonnées cartésiennes .

Description mathématique

Première loi

Première loi de Kepler

La première loi dit: "Le orbite de chaque planète est une ellipse avec le soleil à l'un des foyers. "

Les mathématiques de l'ellipse est la suivante.

L'équation est

$r = \ frac {p} {1+ \ epsilon \ cdot \ cos \ theta}$

où (r, θ) sont coordonnées polaires héliocentriques pour la planète, p est le rectum de semi-latus , et ε est le excentricité, qui est supérieur ou égal à zéro et inférieur à un.

Pour θ = 0 la planète est à la périhélie à distance minimale:

$r_ \ mathrm {min} = \ frac {p} {1+ \ epsilon}$

pour θ = 90 °: r = p et pour θ = 180 ° de la planète est à la aphélie à une distance maximale:

$r_ \ mathrm {max} = \ frac {p} {1- \ epsilon}$

Le demi-grand axe est la moyenne arithmétique entre r et r _{max min:}

$a = \ frac {p} {1- \ epsilon ^ 2}$

Le demi-petit axe est le moyenne géométrique entre r et r _{max min:}

$b = \ frac {p \ sqrt {1- \ epsilon ^ 2}}$

et ce est également le moyenne géométrique entre le demi-grand axe et le demi latus rectum:

$\ Frac a b = \ frac b p$

Deuxième loi

Illustration de la deuxième loi de Kepler.

La deuxième loi: "Une ligne joignant une planète et le soleil balaie des aires égales pendant des intervalles de temps égaux. "

Ce est également connu comme la loi des aires égales. Ce est une conséquence directe de la loi de la conservation du moment cinétique ; voir la dérivation ci-dessous.

Supposons une planète prend un jour pour se rendre de point A à B. Les lignes du Soleil à A et B, ainsi que l'orbite de la planète, vont définir une (environ triangulaire région). Cette même quantité de zone sera formé chaque jour, peu importe où dans son orbite la planète est. Cela signifie que la planète se déplace plus vite quand elle est plus proche du soleil.

Ce est parce que la gravité du soleil accélère la planète comme il tombe vers le soleil, et décélère sur le chemin du retour, mais Kepler ne savait pas que la raison.

Les deux lois autorisés Kepler pour calculer la position, (r, θ), de la planète, basés sur le temps écoulé depuis périhélie, t, et la période orbitale, P. Le calcul se fait en quatre étapes.

1. Calculer l'anomalie moyenne M de la formule

$M = \ frac {2 \ pi t} {P}$

2. Calculer la excentrique anomalie E en résolvant numériquement l'équation de Kepler:

$\ M = E \ epsilon \ cdot \ péché E$

3. Calculer la anomalie vraie θ par l'équation:

$\ Tan \ frac \ theta 2 = \ sqrt {\ frac {1+ \ epsilon} {1- \ epsilon}} \ cdot \ tan \ frac E 2$

4. Calculez la distance r héliocentrique de la première loi:

$r = \ frac {p 1+ \ epsilon \ cdot \ cos \ theta}$

La preuve de cette procédure est illustré ci-dessous.

Troisième loi

La troisième loi: "Le places de la périodes orbitales des planètes sont directement proportionnelle à la cubes de la demi-grand axe de l'orbite. "Ainsi, non seulement ne augmente la longueur de l'orbite avec la distance, la vitesse orbitale diminue, de sorte que l'augmentation de la période orbitale est plus que proportionnelle.

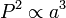
$P ^ 2 \ a ^ 3 propto$

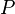$P$ = Période orbitale de la planète

$une$ = Demi-grand axe de l'orbite

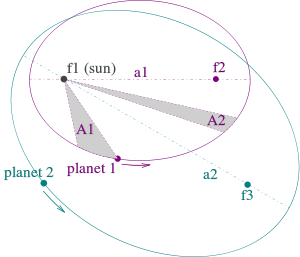
Donc, l'expression P ² · ^-3 a la même valeur pour toutes les planètes dans le système solaire car elle a pour la Terre . Lorsque certaines unités sont choisies, à savoir P est mesurée en années sidérales et un dans unités astronomiques, P ² · ^-3 a la valeur 1 pour toutes les planètes du système solaire.

En Unités SI: 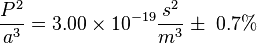$\ Frac {P ^ {2}} {a ^ {3}} = 3,00 \ times 10 ^ {- 19} \ frac {s ^ {2}} {m ^ {3}} \ h \ 0,7% \,$ .

La loi, lorsqu'il est appliqué à orbites circulaires où l' accélération est proportionnelle à une ^-2 · P, montre que l'accélération est proportionnelle à a · un ^{-3 -2} = a, conformément à La loi de la gravitation de Newton.

L'équation générale, que Kepler ne savait pas, est

$\ Gauche ({\ frac {P} {2 \ pi}} \ right) ^ 2 = {a ^ 3 \ over G (M + m)},$

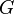où $Sol$ est la constante de gravitation, $M$ est la masse du soleil, et $m$ est la masse de la planète. Celui-ci apparaît dans l'équation puisque l'équation de mouvement comprend la masse réduite. Notez que P est le temps par orbite et P / 2π est temps par radian .

Voir les chiffres réels: attributs des grandes planètes.

Cette loi est également connu comme la loi harmonique.

Position en fonction du temps

Le problème de Kepler suppose une orbite elliptique et les quatre points:

s le soleil (à un foyer d'ellipse);
z périhélie
c le centre de l'ellipse
p la planète

$\ A = | cz |,$ distance du centre de périhélie, le demi-grand axe,

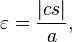$\ \ Varepsilon = {| cs | \ sur une},$ l'excentricité,

$\ B = a \ sqrt {1- \ varepsilon ^ 2},$ les demi-petit axe,

$\ R = | sp |,$ la distance du soleil à la planète.

et l'angle

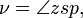$\ Nu = \ angle ZSP,$ comme on le voit la planète du soleil, la anomalie vraie.

Le problème est de calculer les coordonnées polaires (r, ν) de la planète à partir du moment depuis périhélie, t.

Il est résolu par étapes. Kepler a commencé par l'ajout de cercle auxiliaire de l'orbite (que l'axe majeur en tant que diamètre) et définit les points suivants:

x est la projection de la planète du cercle auxiliaire; puis la région $| ZSX | = \ frac un b \ cdot | zsp |$
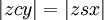
y est un point sur le cercle auxiliaire de telle sorte que la zone $\ | Zcy | = | ZSX |$

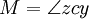$M = \ angle zcy$ , Y vu depuis le centre, le anomalie moyenne.

La superficie de la secteur circulaire $\ | Zcy | = \ frac {a} ^ 2 M 2$ Et l'aire balayée depuis périhélie,

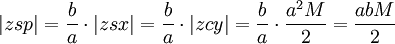$| Zsp | = \ frac ba \ cdot | ZSX | = \ frac ba \ cdot | zcy | = \ frac ba \ cdot \ frac {a} ^ 2 M 2 = \ frac {ab M} {2}$ ,

est par la deuxième loi de Kepler proportionnelle au temps écoulé depuis périhélie. Donc, l'anomalie moyenne, M, est proportionnelle au temps depuis périhélie, t.

$M = {2 \ pi t \ over T},$

où T est la période orbitale.

L'anomalie moyenne M est d'abord calculé. Le but est de calculer la vraie ν d'anomalie. La fonction ν = f (M) est, cependant, pas élémentaire. La solution de Kepler est d'utiliser

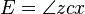$E = \ angle zcx$ , X tel que vu depuis le centre, le anomalie excentrique

comme une variable intermédiaire, et le premier calcul E en fonction de M en résolvant l'équation de Kepler ci-dessous, puis calculer l'anomalie vraie ν de l'anomalie excentrique E. Voici les détails.

$\ | Zcy | = | ZSX | = | zcx | - | SCX |$

$\ Frac {a} ^ 2 M 2 = \ frac {a} ^ 2 E 2- \ frac {a \ varepsilon \ cdot un \ péché E} 2$

Division par un ² / 2 donne l'équation de Kepler

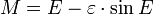$M = E \ varepsilon \ cdot \ péché E$ .

Le hic, ce est que l'équation de Kepler ne peut être réarrangé pour isoler E. La fonction E = f (M) ne est pas une formule élémentaire. L'équation de Kepler est résolu soit itérative par un root-algorithme de recherche ou, comme dérivé dans l'article sur anomalie excentrique, par un série infinie

$E \ approx M + \ left (\ varepsilon- \ frac18 \ varepsilon ^ 3 \ right) \ péché M + \ frac12 \ varepsilon ^ 2 \ péché 2M + \ frac38 \ varepsilon ^ 3 \ sin 3M + \ cdots$

Pour la petite ε typique des planètes (sauf Pluton ), ces séries sont assez précis avec seulement quelques termes.

Ayant calculé l'anomalie excentrique E à partir de l'équation de Kepler, l'étape suivante consiste à calculer l'anomalie vraie ν de l'anomalie excentrique E.

Note de la géométrie du problème que

$un \ cdot \ cos E = a \ cdot \ varepsilon + r \ cdot \ cos \ nu.$

Divisant par un et l'insertion de la première loi de Kepler

$\ \ Frac ra = \ frac {1- \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu}$

obtenir

$\ Cos E = \ varepsilon + \ frac {1- \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu} \ cdot \ cos \ nu = \ frac {\ varepsilon \ cdot (1+ \ varepsilon \ cdot \ cos \ nu) + (1- \ varepsilon ^ 2) \ cdot \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu} = \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}.$

Il en résulte une relation utilisable entre l'anomalie excentrique E et ν de la vraie anomalie.

Un formulaire de calcul plus commode suit en substituant dans le identité trigonométrique:

$\ Tan ^ 2 \ frac {x} {2} = \ frac {1- \ cos x} {1+ \ cos x}.$

Obtenir

$\ Tan ^ 2 \ frac {E} {2} = \ frac {1- \ cos E} {1+ \ cos E} = \ frac {1- \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}} {1+ \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}} = \ frac {(1+ \ varepsilon \ cdot \ cos \ nu) - (\ varepsilon + \ cos \ nu)} {(1+ \ varepsilon \ cdot \ cos \ nu) + (\ varepsilon + \ cos \ nu)} = \ frac {1- \ varepsilon} {1+ \ varepsilon} \ cdot \ frac {1- \ cos \ nu} {1+ \ cos \ nu} = \ frac {1- \ varepsilon} {1+ \ varepsilon} \ cdot \ tan ^ 2 \ frac {\ nu} {2}.$

Multipliant par (1 + ε) / (1-ε) et prenant la racine carrée donne le résultat

$\ Tan \ frac \ nu2 = \ sqrt \ frac {1+ \ varepsilon} {1- \ varepsilon} \ cdot \ tan \ frac E2.$

Nous avons maintenant terminé la troisième étape de la connexion entre le temps et la position dans l'orbite.

On pourrait même développer une série informatique ν directement de M.

La quatrième étape consiste à calculer la distance r heliocentric de l'anomalie vraie ν selon la première loi de Kepler:

$\ R = a \ cdot \ frac {1- \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu}.$

Dérivation à partir des lois de Newton

Les lois de Kepler sont sur le mouvement des planètes autour du soleil, tandis que les lois de Newton sont plus généralement sur le mouvement des particules ponctuelles attirer l'autre par la force de la gravitation . Dans le cas particulier où il n'y a que deux particules, et l'un d'eux est beaucoup plus léger que l'autre, et la distance entre les particules reste limitée, puis la particule se déplace plus légers autour de la particule lourde comme une planète autour du soleil selon les lois de Kepler , comme indiqué ci-dessous. Les lois de Newton mais admettent également d'autres solutions, où la trajectoire de la particule légère est un ou une parabole hyperbole. Ces solutions montrent qu'il existe une limitation de l'applicabilité de la première loi de Kepler, qui stipule que la trajectoire sera toujours une ellipse. Dans le cas où une particule ne est pas beaucoup plus léger que l'autre, il se avère que chaque particule se déplace autour de leur commune centre de masse , de sorte que le grand problème de deux corps est réduit au cas particulier où une particule est beaucoup plus léger que l'autre. Bien que les lois de Kepler sont exprimées en langage géométrique ou équations reliant les coordonnées de la planète et la variable de temps avec le éléments orbitaux, la deuxième loi de Newton est une équation différentielle . Ainsi, les dérivations ci-dessous concernent l'art de résoudre des équations différentielles. La seconde loi est dérivée première, que le calcul de la première loi dépend de la dérivation de la seconde loi.

Issu seconde loi de Kepler

La loi de la gravitation de Newton dit que «chaque objet dans l'univers attire chaque autre objet le long d'une ligne des centres des objets, proportionnelles à la masse de chaque objet, et inversement proportionnelle au carré de la distance entre les objets," et son deuxième loi de motion dit que «les temps de masse, l'accélération est égale à la force." Donc, la masse des satellites fois le vecteur d'accélération de la planète est égale à la masse des temps de chaises la masse de la planète, divisé par le carré de la distance, le temps de moins radial vecteur unitaire, fois une constante de proportionnalité. Ce est écrit:

$m \ cdot \ ddot \ mathbf {r} = \ frac {M \ cdot m} {r ^ 2} \ cdot (- \ hat {\ mathbf {r}}) \ cdot G$

où un point au-dessus de la variable signifie différentiation par rapport au temps, et le second point indique la dérivée seconde.

Supposons que la planète est tellement plus léger que le soleil que l'accélération du soleil peut être négligé.

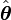$\ Dot \ hat {\ mathbf {r}} = \ dot \ theta \ hat {\ boldsymbol \ theta}$

où $\ Hat {\ boldsymbol \ theta}$ est le vecteur unitaire tangentiel, et

$\ Dot \ hat {\ boldsymbol \ theta} = - \ dot \ theta \ hat {\ mathbf {r}}.$

Ainsi, le vecteur de position

$\ Mathbf {r} = r \ hat {\ mathbf {r}}$

est différenciée deux fois pour donner le vecteur vitesse et le vecteur d'accélération

$\ Dot \ mathbf {r} = \ dot r \ hat \ mathbf {r} + r \ dot \ hat \ mathbf {r} = \ dot r \ hat {\ mathbf {r}} + r \ dot \ theta \ hat {\ boldsymbol \ theta},$

$\ Ddot \ mathbf {r} = (\ ddot r \ hat {\ mathbf {r}} + \ dot r \ dot \ hat {\ mathbf {r}}) + (\ dot r \ dot \ theta \ hat {\ boldsymbol \ theta} + r \ ddot \ theta \ hat {\ boldsymbol \ theta} + r \ dot \ theta \ dot \ hat {\ boldsymbol \ theta}) = (\ ddot r - r \ dot \ theta ^ 2) \ hat {\ mathbf {r}} + (r \ ddot \ theta + 2 \ dot r \ dot \ theta) \ hat {\ boldsymbol \ theta}.$

Notez que pour distance constante, $\ R$ , La planète est soumise à l' accélération centripète , $r \ dot \ theta ^ 2$ Et pour la vitesse angulaire constante, $\ Dot \ theta$ , La planète est soumise à la accélération de Coriolis, $2 \ dot r \ dot \ theta$ .

L'insertion du vecteur d'accélération dans les lois de Newton, et en divisant par m, donne le vecteur équation du mouvement

$(\ Ddot r - r \ dot \ theta ^ 2) \ hat {\ mathbf {r}} + (r \ ddot \ theta + 2 \ dot r \ dot \ theta) \ hat {\ boldsymbol \ theta} = -GMr ^ {- 2} \ hat {\ mathbf {r}}$

Assimiler composant, nous obtenons les deux équations différentielles ordinaires du mouvement, une pour l'accélération radiale et une pour l'accélération tangentielle:

$\ Ddot r - r \ dot \ theta ^ 2 = -GMr ^ {- 2},$

$r \ ddot \ theta + 2 \ dot r \ dot \ theta = 0.$

Afin de tirer seconde loi de Kepler ne l'équation d'accélération tangentielle est nécessaire. Diviser par $\ R \ dot \ theta:$

$\ Frac {\ ddot \ theta} {\ dot \ theta} 2 \ frac {\ dot r} {r} = 0$

et d'intégrer:

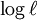$\ Log \ dot \ theta 2 \ log r = \ log \ ell,$

où $\ Log \ ell$ est un constante d'intégration, et exponentiate:

$r ^ 2 \ dot \ theta = \ ell.$

Ce dit que le moment angulaire spécifique 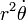$r ^ 2 \ dot \ theta$ est un constante du mouvement, même si les deux la distance $\ R$ et le vitesse angulaire $\ Dot \ theta$ varier.

La zone balayée à partir de l'instant t ₁ à l'instant t _2,

$\ \ Int_ {t_1} ^ {t_2} \ frac 1 2 \ cdot hauteur de base \ de cdot \ cdot dt = \ int_ {t_1} ^ {t_2} \ frac 1 2 \ cdot r \ cdot r \ dot \ theta \ cdot dt = \ frac 1 2 \ cdot \ ell \ cdot (t_2-t_1)$

ne dépend que de la durée t ₂ - t _1. Ce est la deuxième loi de Kepler.

Issu première loi de Kepler

L'expression

$p = \ ell ^ 2 G ^ {- 1} M ^ {- 1}$

a la dimension de longueur et est utilisée pour rendre les équations de mouvement sans dimension. Nous définissons

$\ U = pr ^ {- 1}$

et obtenir

$-GMr ^ {- 2} = - \ ell ^ 2 p ^ {- 3} u ^ {2}$

$\ \ Dot \ theta = \ ell r ^ {- 2} = \ ell p ^ {- 2} u ^ 2.$

La différenciation par rapport au temps est transformé en dérivation par rapport à l'angle:

$\ \ Dot X = \ frac {} {dX d \ theta} \ cdot \ dot \ theta = \ frac {} {dX d \ theta} \ cdot \ ell p ^ {- 2} u ^ 2.$

Différencier

$\ R = pu ^ {- 1}$

deux fois:

$\ Dot r = \ frac {d (pu ^ {- 1})} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ {2} = -pu ^ {- 2} \ frac {} du {d \ theta} \ cdot \ ell p ^ {- 2} u ^ {2} = - \ ell p ^ {- 1} \ frac {du} {d \ theta}$

$\ Ddot r = \ frac {d \ dot r} {d \ theta} \ cdot \ ell p ^ {- 2} u ^ {2} = \ frac {d} {d \ theta} (- \ ell p ^ { -1} \ frac {du} {d \ theta}) \ cdot \ ell p ^ {- 2} u ^ {2} = - \ ell ^ 2 p ^ {- 3} u ^ {2} \ frac {d u ^ 2} {d \ theta ^ 2}$

Substituer dans l'équation radiale de mouvement

$\ Ddot r - r \ dot \ theta ^ 2 = -GMr ^ {- 2}$

et obtenir

$(- \ Ell ^ 2 p ^ {- 3} u ^ 2 \ frac {d ^ 2U} {d \ theta ^ 2}) - (pu ^ {- 1}) (\ ell p ^ {- 2} u ^ 2) ^ 2 = - \ ell ^ 2 p ^ {- 3} u ^ 2$

Divisez par $- \ Ell ^ 2 p ^ {- 3} u ^ 2$ pour obtenir un simple, équation différentielle linéaire non homogène de l'orbite de la planète:

$\ Frac {d ^ 2U} {d \ theta ^ 2} + u = 1.$

Une solution évidente à cette équation est l'orbite circulaire

$\ U = 1.$

D'autres solutions sont obtenues en ajoutant à la solution équation différentielle linéaire homogène à coefficients constants

$\ Frac {d ^ 2U} {d \ theta ^ 2} + u = 0$

Ces solutions sont

$\ U = \ epsilon \ cdot \ cos (\ theta-A)$

où $\ \ Epsilon$ et $\ A$ sont des constantes arbitraires de l'intégration. Donc le résultat est

$\ U = 1+ \ epsilon \ cdot \ cos (\ theta-A)$

Le choix de l'axe de la système de coordonnées tel que 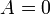$\ A = 0$ Et insertion 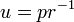$\ U = pr ^ {- 1}$ , Donne:

$\ Pr ^ {- 1} = 1+ \ epsilon \ cdot \ cos \ theta.$

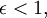Si $\ \ Epsilon <1,$ ce est la première loi de Kepler.

La troisième loi de Kepler

Newton a utilisé la troisième loi comme l'un des éléments de preuve utilisés pour construire le cadre conceptuel et mathématique de sa loi de la gravitation. Si nous prenons les lois du mouvement de Newton comme donné, et d'envisager une hypothétique planète qui se trouve être dans une orbite parfaitement circulaire de rayon r, nous avons $F = mv ^ 2 / r$ pour la force de soleil sur la planète. La vitesse est proportionnelle à r / T, par lequel la troisième loi de Kepler varie comme une au-dessus de la racine carrée de r. En substituant cette dans l'équation de la force, nous constatons que la force gravitationnelle est proportionnelle à une plus r carré. Réelle de la chaîne historique de Newton de raisonnement ne est pas connue avec certitude, parce que dans son écriture, il avait tendance à effacer toute trace de la façon dont il avait atteint ses conclusions. Inversion du sens de raisonnement, nous pouvons considérer cela comme une preuve de la troisième loi de Kepler sur la base de la loi de la gravitation de Newton, et de prendre soin des facteurs de proportionnalité qui ont été négligés dans l'argument ci-dessus, nous avons:

$T ^ 2 = \ frac {4 \ pi ^ 2} {GM} \ cdot r ^ 3$

où:

T = planète de période sidérale
r = rayon de l'orbite circulaire de la planète
G = le constante gravitationnelle
M = masse du soleil

Les mêmes arguments peuvent être appliqués à ne importe quel objet en orbite autour de tout autre objet. Cette discussion suppose implicitement que la planète orbite autour du soleil fixe, mais en réalité, la planète et le soleil tournent autour de leur centre de gravité commun. Newton a reconnu, et a modifié cette troisième loi, notant que la période est également affectée par le corps en orbite autour de la masse . Cependant généralement le corps central est si beaucoup plus massive que la masse du corps en orbite peut être ignoré. Newton a également prouvé que dans le cas d'une orbite elliptique, le demi-grand axe pourrait être remplacé par le rayon. Le résultat le plus général est la suivante:

$T ^ 2 = \ frac {4 \ pi ^ 2} {G (M + m)} \ cdot un ^ 3$

où:

T = objet de période sidérale
d'un objet = demi-grand axe
G = le constante gravitationnelle = 6,67 × 10 ^-11 N • m² / kg²
M = masse d'un objet
m = masse de l'autre objet

Pour les objets en orbite autour du soleil, il peut être pratique d'utiliser des unités d'années, l'UA, et masses solaires, de sorte que G, 4π² et les divers les facteurs de conversion se annulent. Aussi avec m << M nous pouvons mettre en m + M = M, nous avons donc tout simplement 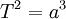$T ^ 2 = a ^ 3$ . Notez que les valeurs de G et masses planétaires ne sont pas connus avec une bonne précision; Toutefois, les produits génétiquement modifiés (l'attraction de Kepler) sont connus pour une précision extrêmement élevée.

Définir le point A à la périastre, et le point B comme apogée de la planète quand orbite du soleil.

La deuxième loi de Kepler indique que le corps en orbite balaie des aires égales dans des quantités égales de temps. Si nous regardons maintenant à un très petites périodes de temps à des moments où la planète est aux points A et B, alors nous pouvons rapprocher la zone balayée par un triangle avec une altitude égale à la distance entre la planète et le soleil, et la base égale à l'époque de temps la vitesse de la planète.

$\ Begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot (1- \ epsilon) a \ cdot V_A \, dt = \ begin {matrix} \ frac {1} {2} \ end { matrix} \ cdot (1+ \ epsilon) a \ cdot V_B \, dt$

$(1- \ epsilon) \ cdot V_A = (1+ \ epsilon) \ cdot V_B$

$V_A = V_B \ cdot \ frac {1+ \ epsilon} {1- \ epsilon}$

En utilisant le loi de conservation de l'énergie pour l' énergie totale de la planète aux points A et B,

$\ Frac {mV_A ^ 2} {2} - \ frac {} {GmM (1- \ epsilon) a} = \ frac {mV_B ^ 2} {2} - \ frac {} {GmM (1+ \ epsilon) un }$

$\ Frac {V_A ^ 2} {2} - \ frac {V_B ^ 2} {2} = frac {} {GM (1- \ epsilon) a} \ - \ frac {} {GM (1+ \ epsilon) un }$

$\ Frac {V_A ^ 2-V_B ^ 2} {2} = \ frac {} GM {a} \ cdot \ left (\ frac {1} {(1- \ epsilon)} - \ frac {1} {(1 + \ epsilon)} \ right)$

$\ Frac {\ left (V_B \ cdot \ frac {1+ \ epsilon} {1- \ epsilon} \ right) ^ 2-V_B ^ 2} {2} = \ frac {} GM {a} \ cdot \ left ( \ frac {1+ \ epsilon-1 + \ epsilon} {(1- \ epsilon) (1+ \ epsilon)} \ right)$

$V_B ^ 2 \ cdot \ left (\ frac {1+ \ epsilon} {1- \ epsilon} \ right) ^ 2-V_B ^ 2 = \ frac {} 2GM {a} \ cdot \ left (\ frac {2 \ epsilon} {(1- \ epsilon) (1+ \ epsilon)} \ right)$

$V_B ^ 2 \ cdot \ left (\ frac {(1+ \ epsilon) ^ 2- (1- \ epsilon) ^ 2} {(1- \ epsilon) ^ 2} \ right) = \ frac {4GM \ epsilon} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B ^ 2 \ cdot \ left (\ frac {1 + 2 \ epsilon + \ epsilon ^ 2-1 + 2 \ epsilon \ epsilon ^ 2} {(1- \ epsilon) ^ 2} \ right) = \ frac {4GM \ epsilon} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B ^ 2 \ cdot 4 \ epsilon = \ frac {4GM \ epsilon \ cdot (1- \ epsilon) ^ 2} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B = \ sqrt {\ frac {GM \ cdot (1- \ epsilon)} {a \ cdot (1+ \ epsilon)}}.$

Maintenant que nous avons 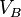$V_B$ , Nous pouvons trouver la vitesse à laquelle la planète balaie sur zone dans l'ellipse. Ce taux reste constante, donc nous pouvons dériver de ne importe quel point nous voulons, en particulier du point B.

$\ Frac {} {dA dt} = \ frac {\ frac {1} {2} \ cdot (1+ \ epsilon) a \ cdot V_B \, dt} {dt} = \ begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot (1+ \ epsilon) a \ cdot V_B$

$= \ Begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot (1+ \ epsilon) a \ cdot \ sqrt {\ frac {GM \ cdot (1- \ epsilon)} {a \ cdot (1+ \ epsilon)}} = \ begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot \ sqrt {GMa \ cdot (1- \ epsilon) (1+ \ epsilon)}$

Cependant, la surface totale de l'ellipse est égale à $\ Pi un \ sqrt {(1- \ epsilon ^ 2)} une$ . (Ce est la même chose que 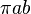$\ Pi a b$ , Parce $b = \ sqrt {(1- \ epsilon ^ 2)} une$ ). Le temps de la planète sortir pour balayer toute la zone de l'ellipse est égale à l'aire de l'ellipse, de sorte,

$T \ cdot \ frac {} {dA dt} = \ pi un \ sqrt {(1- \ epsilon ^ 2)} une$

$T \ cdot \ begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot \ sqrt {GMa \ cdot (1- \ epsilon) (1+ \ epsilon)} = \ pi \ sqrt {(1 - \ epsilon ^ 2)} a ^ 2$

$T = \ frac {2 \ pi \ sqrt {(1- \ epsilon ^ 2)} a ^ 2} {\ sqrt {GMa \ cdot (1- \ epsilon) (1+ \ epsilon)}} = \ frac {2 \ pi a ^ 2} {\ sqrt {}} GMa = \ frac {2 \ pi} {\ sqrt {GM}} \ sqrt {a} ^ 3$

$T ^ 2 = \ frac {4 \ pi ^ 2} {} GM a ^ 3.$

Toutefois, si la masse m ne est pas négligeable par rapport à M, alors la planète orbite le soleil avec la même vitesse et la position exacte comme un très petit corps en orbite un objet de masse $M m +$ (Voir masse réduite). Pour intégrer que dans la formule ci-dessus, M doit être remplacé par $M m +$ , Donner

$T ^ 2 = \ frac {4 \ pi ^ 2} {G (M + m)} a ^ 3.$

CQFD

Récupéré à partir de " http://en.wikipedia.org/w/index.php?title=Kepler%27s_laws_of_planetary_motion&oldid=198683410 "

Privacy Policy and Contacts (IT)