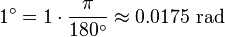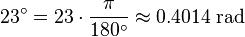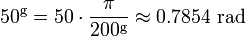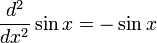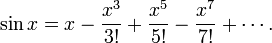Radian

Certains angles communs, mesurée en radians. Tous les polygones sont des polygones réguliers.

Le radian est une unité de plan angle , égal à 180 / π degrés , soit environ 57,2958 degrés. Ce est l'unité de mesure standard angulaire dans tous les domaines de mathématiques au-delà du niveau élémentaire.

Le radian est représenté par le symbole «rad» ou, plus rarement, par le c exposant (pour "mesure circulaire»). Par exemple, un angle de 1,2 radians serait écrit que "1,2 rad" ou "1.2 ^c" (le deuxième symbole peut être confondu avec un degré: «1,2 °»). Toutefois, le radian est mathématiquement considérée comme un «nombre pur" qui n'a pas besoin symbole de l'unité, et par écrit mathématique le symbole «rad» est presque toujours omis. En l'absence de toute radians de symboles sont pris en charge, et quand degrés visent le symbole Est utilisé.

Le radian était auparavant SI unité supplémentaire, mais cette catégorie a été aboli en 1995 et le radian est maintenant considéré comme un SI dérivées unité. L'unité SI de mesure de l'angle solide est la stéradian.

Définition

Un angle de 1 radian sous-tend un arc de longueur égale à la rayon du cercle .

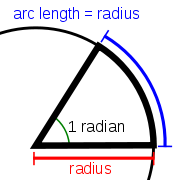
Un radian est l' angle sous-tendu au centre d'un cercle par un arc de circonférence qui est égale en longueur à la rayon du cercle.

Plus généralement, l'amplitude en radians de ne importe quel angle sous-tendu par deux rayons est égale au rapport de la longueur de l'arc fermé au rayon du cercle; ce est-à θ = l / r, où θ est l'angle sous-tendu en radians, s est la longueur d'arc, et r est le rayon. Inversement, la longueur de l'arc est fermée égal au rayon multiplié par la valeur de cet angle en radians; ce est, s = rθ.

Il se ensuit que la grandeur en radians d'un tour complet (360 °) est la longueur de la totalité de la circonférence divisée par le rayon, ou 2π r / r, ou 2π. Ainsi 2π radians est égale à 360 degrés, ce qui signifie une radian est égal à 180 / π degrés.

Histoire

Le concept de radians, par opposition à la mesure d'un angle, devrait probablement être crédité sur Roger Cotes en 1714. Il avait le radian dans tout sauf le nom, et il a reconnu son naturel comme une unité de mesure angulaire.

Le terme est apparu en radian impression sur 5 juin 1873 , dans les questions d'examen établi par James Thomson (frère de Lord Kelvin ) au Collège Queen, Belfast . Il a utilisé le terme dès 1871, alors que en 1869, Thomas Muir, puis de l' Université de St Andrews , hésitait entre rad, radial et radian. En 1874 , Muir a adopté radian après une consultation avec James Thomson.

Conversions

Conversion entre les radians et les degrés

Comme indiqué plus haut, une radian est égal à 180 / π degrés. Ainsi, pour convertir de radians en degrés, multiplier par 180 / π. Par exemple,

A l'inverse, pour convertir les degrés en radians, multiplier par π / 180. Par exemple,

Vous pouvez également convertir des radians en révolutions en divisant nombre de radians par 2π.

Le tableau montre la conversion de certains angles communs.

Degrés	0 °	30 °	45 °	60 °	90 °	180 °	270 °	360 °
Radians	0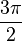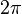

Conversion entre radians et les grades

2π radians sont égales à une révolution complète, qui est de 400 ^g. Alors, pour convertir de radians à diplômés multiplier par 200 / π, et de convertir les diplômés en radians multiplier par π / 200. Par exemple,

Raisons pour lesquelles radians sont préférés en mathématiques

Dans le calcul et la plupart des autres branches des mathématiques au-delà de la géométrie pratique, les angles sont mesurés en radians universellement. Ce est parce que radians ont un «naturel» mathématique qui conduit à une formulation plus élégante d'un certain nombre de résultats importants.

Plus particulièrement, les résultats de l'analyse portant sur les fonctions trigonométriques sont simples et élégant quand les arguments des fonctions sont exprimés en radians. Par exemple, l'utilisation de radians conduit à la simple limite formule

,

qui est la base de beaucoup d'autres identités en mathématiques, y compris

En raison de ceux-ci et d'autres propriétés, les fonctions trigonométriques apparaissent dans des solutions à des problèmes mathématiques qui ne sont pas évidemment liées à significations géométriques des fonctions (par exemple, les solutions de l'équation différentielle d ² y / dx ² = - y, l'évaluation de l'intégrale ∫ dx / (1 + x ^2), et ainsi de suite). Dans tous ces cas, il se trouve que les arguments aux fonctions sont plus naturellement écrites sous la forme qui correspond, dans des contextes géométriques, à la mesure des angles radians.

Les fonctions trigonométriques ont en outre des extensions simples et élégantes de la série lorsque radians sont utilisés; par exemple, ce qui suit la série de Taylor pour le péché x:

Si x ont été exprimées en degrés alors la série contiendra facteurs désordre impliquant pouvoirs de π / 180: si x est le nombre de degrés, le nombre de radians est y = x π / 180, de sorte

Mathématiquement relations importantes entre le sinus et le cosinus et la fonction exponentielle (voir, par exemple, La formule d'Euler) sont, à nouveau, élégant quand les arguments des fonctions sont en radians et désordre autrement.

Analyse dimensionnelle

Bien que le radian est une unité de mesure, ce est un grandeur sans dimension. Ceci peut être vu à partir de la définition donnée plus haut: l'angle sous-tendu au centre d'un cercle, mesurée en radians, est le rapport de la longueur de l'arc fermé à la longueur du rayon du cercle. Depuis les unités de mesure se annulent, ce rapport est sans dimension.

Une autre façon de voir le dimensionlessness du radian est dans les représentations de la série des fonctions trigonométriques, comme la série de Taylor pour le péché x mentionné précédemment:

Si x avait unités, alors la somme serait vide de sens: le terme linéaire x ne peut pas être ajouté à (ou ont soustrait) du terme cubique ou le terme quintique 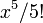, Etc. Par conséquent, x doivent être sans dimension.

Utilisation dans la physique

Le radian est largement utilisé en physique lorsque les mesures angulaires sont nécessaires. Par exemple, la vitesse angulaire est généralement mesurée en radians par seconde (rad / s). Un tour par seconde est égale à 2π radians par seconde.

De même, accélération angulaire est souvent mesurée en radians par seconde par seconde (rad / s ^2).

Les raisons sont les mêmes que pour les mathématiques.

Multiples d'unités radian

Préfixes métriques ont une utilisation limitée avec radians, et aucun en mathématiques.

Le milliradian (0,001 rad, ou une mrad) est utilisé dans artillerie et ciblage, car elle correspond à une erreur de 1 m à une distance de 1 000 m (à ces petits angles, la courbure est négligeable). Le divergence de laser poutres est également généralement mesurée en milliradians.

Les petites unités comme microradians (μrads) et nanoradians (nrads) sont utilisés en astronomie, et peuvent également être utilisés pour mesurer la qualité du faisceau de lasers ultra-faible divergence. De même, les préfixes plus petite que milli- sont potentiellement utiles dans la mesure de très petits angles.

Cependant, les préfixes plus grands ont aucune utilité apparente, principalement en raison de dépasser 2π radians est de commencer le même cercle (ou cycle révolutionnaire) à nouveau.