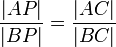Cercle
Renseignements généraux
Ce contenu de Wikipedia a été sélectionné par SOS Enfants d'aptitude dans les écoles à travers le monde. Cliquez ici pour en savoir plus sur le parrainage d'enfants.
| Cercle | |
|---|---|
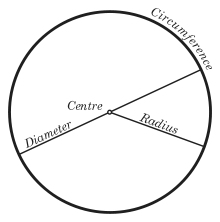 Cercle illustration montrant un rayon, un diamètre, le centre et la circonférence | |
| Zone |  (Où r = rayon) (Où r = rayon) |

Un cercle est simple forme de la géométrie euclidienne qui est l'ensemble de tous points dans un plan qui sont à une distance donnée d'un point donné, la centre. La distance entre chacun des points et le centre est appelé le rayon. Elle peut aussi être définie comme le lieu géométrique d'un point équidistant d'un point fixe.
Un cercle est une simple fermée courbe qui divise le plan en deux régions: une intérieur et un extérieur. En utilisation quotidienne, le terme «cercle» peut être utilisé indifféremment pour désigner soit de la limite de la figure, ou à la figure entière, y compris son intérieur; dans l'usage strictement technique, le cercle est l'ancien et celui-ci est appelé disque.
Un cercle peut être définie comme la courbe tracée par un point qui se déplace afin que sa distance à un point donné est constant.
Un cercle peut également être définie comme une spéciale ellipse dans laquelle les deux foyers sont confondus et la excentricité est 0. Les cercles sont les sections coniques atteint quand un cône circulaire droit est coupée par un plan perpendiculaire à l'axe du cône.
Terminologie
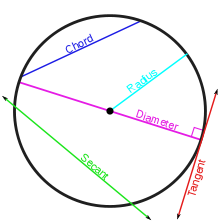
- Arc: toute partie connexe de la circonférence du cercle.
- Centre: le point équidistant des points sur la circonférence.
- Chord: un segment de droite dont les points d'extrémité situés sur le cercle.
- Circonférence: la longueur d'un circuit le long du cercle.
- Diamètre : la plus longue corde, un segment de droite dont les extrémités se trouvent sur le cercle et qui passe par le centre; ou la longueur d'un tel segment, qui est la plus grande distance entre deux points quelconques sur le cercle.
- Radius: un segment de droite reliant le centre du cercle pour ne importe quel point sur le cercle lui-même; ou la longueur d'un tel segment, qui est un demi diamètre.
- Secant: un accord étendu, une ligne droite coupe le cercle en deux points.
- Secteur: une région délimitée par deux rayons et un arc se étendant entre les rayons.
- Segment: une région délimitée par une corde et un arc se étendant entre les extrémités de la corde.
- Demi-cercle: une région délimitée par un diamètre et un arc se étendant entre les points d'extrémité de la diamètre. Ce est un cas particulier d'un segment.
- Tangent : une ligne droite qui touche le cercle en un point unique.
 |
 |
Histoire
Le mot «cercle» dérive du grec, kirkos "un cercle," de la KER de base qui signifie tourner ou plier. Les origines des mots " Circus "et" circuit "sont étroitement liés.

Le cercle est connu depuis avant le début de l'histoire enregistrée. Cercles naturelles auraient été observés, comme la Lune, le Soleil, et une tige de plante très courte dans le vent sur le sable, qui constitue une forme de cercle dans le sable. Le cercle est la base de la roue , qui, avec des inventions connexes tels que engrenages, fait une grande partie de la machinerie moderne possible. En mathématiques, l'étude du cercle a aidé à inspirer le développement de la géométrie, l'astronomie , et le calcul.
Au début la science , en particulier la géométrie et astrologie et l'astronomie, a été relié au divin pour la plupart savants médiévaux, et beaucoup croyaient qu'il y avait quelque chose d'intrinsèquement «divine» ou «parfait» qui pourrait être trouvé dans les cercles.
 Le boussole dans ce manuscrit du 13ème siècle est un symbole de l'acte de Dieu Création. Notez également la forme circulaire de la halo
Le boussole dans ce manuscrit du 13ème siècle est un symbole de l'acte de Dieu Création. Notez également la forme circulaire de la halo
 Tughrul Tour de l'intérieur
Tughrul Tour de l'intérieur
 Cercles sur un vieux dessin astronomique arabe
Cercles sur un vieux dessin astronomique arabe
Parmi les faits saillants de l'histoire du cercle sont:
- 1700 BCE - Le Papyrus Rhind donne une méthode pour trouver la surface d'un champ circulaire. Le résultat correspond à 256/81 (3,16049 ...) en tant que valeur approximative de π.
- 300 BCE - Livre 3 Éléments d'Euclide traite des propriétés du cercle.
- Dans Platon s ' Seventh Letter il ya une définition détaillée et une explication du cercle. Platon explique le cercle parfait, et comment il est différent de ne importe quel dessin, les mots, la définition ou une explication.
- 1880 CE- Lindemann prouve que π est transcendant, régler efficacement le problème de millénaire de la quadrature du cercle.
Résultats analytiques
Longueur de circonférence
Le rapport de cercle de circonférence à son diamètre est π (pi), un irrationnelle constante approximativement égale à 3,141592654. Ainsi, la longueur de la circonférence C est liée à la rayon r et de diamètre D par:
Espace clos

Comme l'a montré par Archimède, le zone délimitée par un cercle est égale à celle d'un triangle dont la base a la longueur de la circonférence du cercle et dont la hauteur est égale au rayon du cercle, qui vient à π multiplié par le rayon au carré:
De manière équivalente, en désignant diamètre d,
soit environ 79 pour cent de la carré circonscrit (dont le côté est de longueur d).
Le cercle est la courbe plane entourant la surface maximale pour une longueur d'arc donné. Il se agit du cercle à un problème dans le calcul des variations , à savoir la isopérimétrique inégalités.
Équations
Les coordonnées cartésiennes

Dans un x - y système de coordonnées cartésiennes , le cercle de centre Les coordonnées (a, b) et le rayon r est l'ensemble de tous les points (x, y) de sorte que
Cette équation , aussi connu comme équation du cercle, découle du théorème de Pythagore appliqué à ne importe quel point sur le cercle: comme le montre le schéma de droite, le rayon est l'hypoténuse d'un triangle rectangle dont les côtés sont de longueur autre x - A et Y - b. Si le cercle est centré à l'origine (0, 0), l'équation se simplifie
L'équation peut être écrite dans forme paramétrique en utilisant l' fonctions trigonométriques sinus et cosinus
où t est un paramétrique variables dans la plage de 0 à 2π, interprétée géométriquement comme étant l'angle que le rayon de (a, b) à (x, y) fait avec l'axe des x. Une alternative paramétrage du cercle est:
Dans ce paramétrage, le rapport de t à r peut être interprétée comme la géométriquement projection stéréographique de cercle sur la droite passant par le centre parallèle à l'axe des x.
En coordonnées homogènes chaque section conique avec l'équation d'un cercle est de la forme
Il peut être prouvé qu'une section conique est un cercle exactement quand il contient (lorsqu'il est étendu à la plan projectif complexe) les points que je (1: i: 0) et J (1: - i: 0). Ces points sont appelés les Points cycliques.
Les coordonnées polaires
En coordonnées polaires l'équation d'un cercle est:
où a est le rayon du cercle,  est la coordonnées polaires d'un point générique sur le cercle, et
est la coordonnées polaires d'un point générique sur le cercle, et 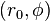 est la coordonnée polaire du centre du cercle (à savoir, r 0 est la distance de l'origine au centre du cercle, et φ est l'angle de sens anti-horaire à partir de l'axe des x x positif à la ligne reliant l'origine au centre de le cercle). Pour un cercle centré à l'origine, soit R 0 = 0, ce qui réduit simplement à r = a. Quand R 0 = un, ou lorsque l'origine est sur le cercle, l'équation devient
est la coordonnée polaire du centre du cercle (à savoir, r 0 est la distance de l'origine au centre du cercle, et φ est l'angle de sens anti-horaire à partir de l'axe des x x positif à la ligne reliant l'origine au centre de le cercle). Pour un cercle centré à l'origine, soit R 0 = 0, ce qui réduit simplement à r = a. Quand R 0 = un, ou lorsque l'origine est sur le cercle, l'équation devient
Dans le cas général, l'équation peut être résolue pour r, ce qui donne
la solution avec un signe moins devant la racine carrée donnant la même courbe.
Plan complexe
Dans le plan complexe , un cercle de centre c et au rayon (r) a pour équation  . Dans cette forme paramétrique peut être écrit
. Dans cette forme paramétrique peut être écrit  .
.
L'équation légèrement généralisée  pour de vrai p, q et g complexe est parfois appelé cercle généralisée. Cela devient l'équation ci-dessus pour un cercle avec
pour de vrai p, q et g complexe est parfois appelé cercle généralisée. Cela devient l'équation ci-dessus pour un cercle avec  Car
Car  . Pas tous les milieux généralisées sont en fait des cercles: un cercle généralisée est soit un (vrai) cercle ou une ligne .
. Pas tous les milieux généralisées sont en fait des cercles: un cercle généralisée est soit un (vrai) cercle ou une ligne .
tangentes
La tangente passant par un point P sur le cercle est perpendiculaire au diamètre passant par P. Si P = (x 1, y 1) et le centre cercle a (a, b) et de rayon r, alors la tangente est perpendiculaire à la ligne à partir de (a, b) à (x 1, y 1), de sorte qu'il a la forme (x 1 - a) x + (y 1 - y) b = c. L'évaluation au (x 1, y 1) détermine la valeur de c et le résultat est que l'équation de la tangente est
ou
Si y 1 ≠ B, alors la pente de cette ligne est
Cela peut également être trouvée en utilisant la différenciation implicite.
Lorsque le centre du cercle est à l'origine de l'équation de la ligne tangente devient
et sa pente est
Propriétés
- Le cercle est la forme la plus grande surface pour une longueur donnée de périmètre. (Voir Théorème isopérimétrique.)
- Le cercle est une forme très symétrique: chaque ligne par le centre forme une ligne de symétrie de réflexion et il a symétrie de rotation autour du centre pour chaque angle. Son groupe de symétrie est le groupe orthogonal O (2, R). Le groupe des rotations est le seul groupe de cercle T.
- Tous les cercles sont similaire.
- La circonférence et le rayon d'un cercle sont proportionnelle.
- La zone fermée et le carré de son rayon sont proportionnelle.
- Le constantes de proportionnalité sont 2π et π respectivement.
- Le cercle qui est centré à l'origine de rayon 1 est appelé cercle unité.
- Considéré comme un grand cercle de la sphère unité, il devient le Cercle de Riemann.
- Grâce à trois points quelconques, pas tous sur la même ligne, il se trouve un cercle unique. En coordonnées cartésiennes , il est possible de donner des formules explicites pour les coordonnées du centre du cercle et le rayon en termes de coordonnées des trois points donnés. Voir circonscrit.
Corde
- Les accords sont à égale distance du centre d'un cercle si et seulement si elles sont égales en longueur.
- La médiatrice d'une corde passe par le centre d'un cercle; déclarations équivalentes découlant de l'unicité de la médiatrice:
- Une ligne perpendiculaire au centre d'un cercle bissecte la corde.
- Le segment de ligne ( segment de cercle) à travers le centre d'une corde bissecteur est perpendiculaire à la corde.
- Si un angle central et un angle inscrit d'un cercle sont sous-tendu par la même corde et sur le même côté de la corde, l'angle au centre est le double de l'angle inscrit.
- Si deux angles sont inscrits sur la même membrure et sur le même côté de la corde, ils sont égaux.
- Si deux angles sont inscrits sur la même membrure et sur des côtés opposés de la corde, ils sont complémentaires.
- Pour un quadrilatère cyclique, l'angle extérieur est égal à l'angle intérieur opposé.
- Un angle inscrit sous-tendu par un diamètre est un angle droit (voir Thales théorème).
- Le diamètre est la plus longue corde du cercle.
- Si l'intersection de deux des accords divise une corde en longueurs A et B et divise l'autre corde en longueurs c et d, puis ab = cd.
- Si l'intersection de deux des accords perpendiculaires divise une corde en longueurs A et B et divise l'autre corde en longueurs c et d, puis une 2 + 2 b + c 2 + d 2 est égale au carré du diamètre.
- La somme des carrés des longueurs des cordes des deux coupant à angle droit en un point donné est la même que celle des deux autres cordes se coupent en un même point, et est donné par r 8 2-4 2 p (où r est le le rayon de cercle et p est la distance du point au point d'intersection) de centre.
- La distance d'un point sur le cercle à une fois d'accords donnés le diamètre du cercle est égal au produit des distances du point aux extrémités de la corde.
Sagitta
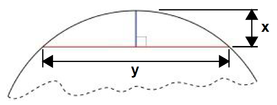
- Le sagitta (également connu sous le nom Versine) est un segment de droite tracée perpendiculairement à un accord, entre le point milieu de cette corde et l'arc de cercle.
- Compte tenu de la longueur y d'un accord, et la longueur x du Sagitta, le théorème de Pythagore peut être utilisé pour calculer le rayon du cercle unique qui se adapte autour des deux lignes:
Une autre preuve de ce résultat qui ne repose que sur deux propriétés d'accords indiquées ci-dessus est le suivant. Étant donné une corde de longueur et y sagitta de longueur x, depuis le sagitta croise le milieu de la corde, nous savons que ce est une partie d'un diamètre du cercle. Comme le diamètre est deux fois le rayon, la partie «manquant» est le diamètre (r 2 - x) de longueur. En utilisant le fait que une partie d'une fois de membrure l'autre partie est égal au même produit, prise le long d'une corde coupant la première corde, on constate que (r 2 - x) = x (y / 2) 2. Résolution pour r, nous trouvons le résultat requis.
Tangente
- Le tracé perpendiculaire à un rayon passant par le point du rayon d'extrémité est tangente à un cercle.
- Une ligne tracée perpendiculaire à une tangente passant par le point de contact avec un cercle passant par le centre du cercle.
- Deux tangentes peuvent toujours être attirés par un cercle de tout point en dehors du cercle, et ces tangentes sont égaux en longueur.
- Si une tangente en A et une tangente en B se coupent au point extérieur P, puis désignant le centre que O, les angles ∠ BOA et ∠ BPA sont supplémentaire.
- Si AD est tangente au cercle en A et si AQ est une corde du cercle, alors ∠ DAQ = 1/2 arc (AQ).
Théorèmes

- Le théorème d'accord stipule que si deux accords, CD et EB, se coupent en A, puis CA × DA = EA × BA.
- Si une tangente d'un point D externe répond le cercle au C et un sécant du point D externe répond le cercle en G et E respectivement, puis DC = 2 × DG DE. (Théorème de Tangent-sécant.)
- Si deux sécantes, DG et DE, ont également réduit le cercle au H et F, respectivement, alors DH × DG = DF × DE. (Corollaire du théorème de la tangente-sécante.)
- L'angle entre une tangente et la corde est égale à une moitié de l'angle sous-tendu sur le côté opposé de la membrure (Tangent Jaquette Angle).
- Si l'angle sous-tendu par la corde au centre est de 90 degrés , alors L = √2 r, où l est la longueur de la corde et r est le rayon du cercle.
- Si deux sécantes sont inscrits dans le cercle comme illustré à droite, la mesure de l'angle A est égal à la moitié de la différence des mesures des arcs fermés (DE) et la Colombie-Britannique. Ce est le théorème sécante sécant.
Les angles inscrits
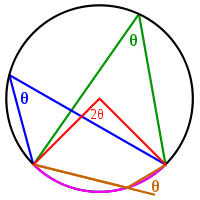
Une angle inscrit (exemples sont les angles bleu et vert sur la figure) est exactement la moitié du correspondant angle au centre (rouge). Par conséquent, tous les angles inscrits qui sous-tendent le même arc (rose) sont égaux. Angles inscrits sur l'arc (marron) sont complémentaires. En particulier, tout angle inscrit qui sous-tend un diamètre est un angle droit (depuis l'angle au centre est de 180 degrés).
Cercle d'Apollonius
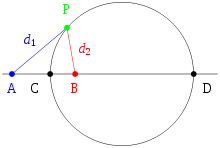
Apollonius de Perga montré qu'un cercle peut également être définie comme l'ensemble des points dans un plan, ayant un rapport constant (autre que 1) des distances à deux foyers fixes A et B. (L'ensemble des points où les distances sont égales est la médiatrice de A et B, une ligne.) Ce cercle est dit parfois à tirer environ deux points.
La preuve est en deux parties. Premièrement, il faut prouver que, compte tenu de deux foyers A et B et un rapport de distances, tout point P satisfaisant le rapport des distances doit tomber sur un cercle particulier. Soit C un autre point, satisfaisant également le rapport et couché sur le segment AB. Par le bissectrice théorème le segment de ligne PC va couper la intérieur angle APB, depuis les secteurs sont similaires:
De manière analogue, un PD segment de droite passant par un point D sur AB étendu divise le correspondant angle extérieur BPQ où Q est sur AP prolongée. Depuis les angles intérieurs et extérieurs résument à 180 degrés, l'angle CPD est exactement 90 degrés, soit un angle droit. L'ensemble des points P tels que angle CPD est un angle droit forme un cercle, dont le CD est un diamètre.
Deuxièmement, voir une preuve que chaque point sur le cercle indiqué satisfait du rapport donné.
Croix-ratios
Une propriété très proche de cercles implique la géométrie de la birapport de points dans le plan complexe . Si A, B, et C sont tels que ci-dessus, puis le cercle d'Apollonius pour ces trois points est l'ensemble des points P pour lequel la valeur absolue de la traverse rapport est égal à une:
En d'autres termes, P est un point sur le cercle d'Apollonius si et seulement si le birapport [A, B, C, P] est le cercle unité dans le plan complexe.
Cercles généralisées
Si C est la milieu du segment AB, puis la collecte de points P satisfaisant à la condition qu'Apollonius
ne est pas un cercle, mais une ligne.
Ainsi, si A, B et C sont donnés points distincts dans le plan, le lieu des points P satisfaisant à l'équation ci-dessus est appelé un "cercle généralisée." Il peut être soit un vrai cercle ou une ligne. Dans ce sens, une ligne est un cercle généralisée de rayon infini.
Cercles inscrits ou circonscrites sur les autres chiffres
Dans chaque triangle , un cercle unique, appelée la cercle inscrit, peut se inscrire de sorte qu'il est tangent à chacun des trois côtés du triangle.
A propos de tout triangle, un cercle unique, appelée la cercle circonscrit, peut être circonscrit de telle sorte qu'il passe par chacune des triangle de trois sommets.
Un polygone tangentielle, tel qu'un quadrilatère tangentielle, est tout polygone convexe à l'intérieur d'un cercle qui peut être inscrit qui est tangent à chaque côté du polygone.
Un polygone cyclique est tout polygone convexe autour duquel un cercle peut être circonscrit, en passant par chaque sommet. Un exemple bien étudié est le quadrilatère cyclique.
Un hypocycloïde est une courbe qui se inscrit dans un cercle donné en traçant un point fixe sur un plus petit cercle qui roule à l'intérieur et tangente au cercle donné.
Cercle comme limitant cas d'autres chiffres
Le cercle peut être considérée comme un cas limite de chacun des divers autres chiffres:
- Un Ovale cartésienne est un ensemble de points tels que A somme pondérée des distances des points de l'un de ses deux points fixes ( foyers) est une constante. Une ellipse est le cas dans lequel les pondérations sont égales. Un cercle est une ellipse avec un excentricité de zéro, ce qui signifie que les deux foyers coïncident les uns avec les autres en tant que centre du cercle. Un cercle est également un cas particulier différent d'un ovale cartésien dans lequel l'un des poids est égal à zéro.
- Un superellipse a une équation de la forme
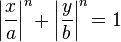 pour le positif a, b, et n. Un supercircle a b = a. Un cercle est le cas particulier d'un supercircle dans laquelle n = 2.
pour le positif a, b, et n. Un supercircle a b = a. Un cercle est le cas particulier d'un supercircle dans laquelle n = 2. - Un Cassini ovale est un ensemble de points tels que le produit de la distance entre ne importe quel de ses points à deux points fixes est une constante. Lorsque les deux points fixes coïncident, un des résultats de cercle.
- Un courbe de largeur constante est un chiffre dont la largeur, définie comme la distance perpendiculaire entre deux lignes parallèles distinctes se coupent sa limite en un point unique, est le même quel que soit le sens de ces deux lignes parallèles. Le cercle est l'exemple le plus simple de ce type de figure.


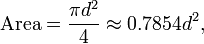

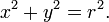

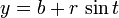
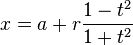
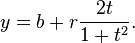

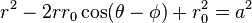

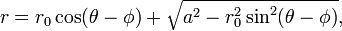
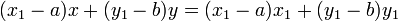

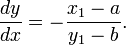


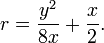

![| [A, B, C, P] | = 1. \](../../images/2039/203983.png)