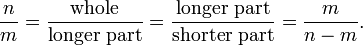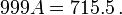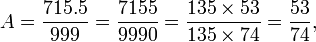Nombre irrationnel

En mathématiques , un nombre irrationnel est ne importe quel nombre réel qui ne est pas un nombre rationnel - autrement dit, il se agit d'un nombre qui ne peut être exprimée comme une fraction m / n, où m et n sont des nombres entiers , avec n différent de zéro. Officieusement, cela signifie numéros qui ne peuvent pas être représentés comme des fractions simples. On peut en déduire qu'ils ont également ne peuvent pas être représentés comme fin ou nombres décimaux, mais l'idée est plus profond que cela. Bien qu'il puisse sembler étrange au premier abord audience, presque tous les nombres réels sont irrationnelles, dans un sens qui est défini plus précisément ci-dessous. Peut-être que les numéros les plus connus sont irrationnel π et √2.

Quand le rapport des longueurs des deux segments de ligne est irrationnel, les segments de ligne sont également décrits comme étant incommensurable, ce qui signifie qu'ils ne partagent aucune mesure en commun. Une mesure d'un segment de la ligne I est dans ce sens un segment de droite que J "mesures" I dans la mesure où un nombre de copies de l'ensemble J fixées bout à bout occupent la même longueur que je.

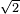Le numéro est irrationnel.

Histoire

La première preuve de l'existence de nombres irrationnels est généralement attribuée à Hippasus de Métaponte, un Pythagore qui a probablement découvert tout en identifiant les côtés de la pentagramme. Cependant Pythagore croyait en l'absolu de numéros, et ne pouvait pas accepter l'existence de nombres irrationnels. Il ne pouvait pas infirmer leur existence à travers la logique, mais ses convictions ne serait pas accepter l'existence de nombres irrationnels et donc, que la légende l'avait, il avait Hippasus noyé. Théodore de Cyrène prouva l'irrationalité de la surds de nombres entiers jusqu'à 17, mais se arrêtaient là probablement parce que l'algèbre qu'il a utilisé ne pouvait pas être appliquée à la racine carrée de 17. Ce ne est que Eudoxe développé une théorie de rapports irrationnels qu'une base solide mathématique des nombres irrationnels a été créé. Éléments d'Euclide livre 10 est dédiée à la classification des grandeurs irrationnelles.

Le XVIe siècle a vu l'acceptation de négatifs , intégrales et fractions numéros. Le XVIIe siècle a vu fractions décimales avec la notation moderne assez généralement utilisé par les mathématiciens. Les cent prochaines années ont vu les nombres imaginaires deviennent un outil puissant dans les mains de Abraham de Moivre, et surtout de Leonhard Euler . L'achèvement de la théorie des nombres complexes dans le XIXe siècle a entraîné la différenciation des irrationnels en nombres algébriques et transcendantes, la preuve de l'existence de nombres transcendants, et la résurgence de l'étude scientifique de la théorie des irrationnels, largement ignorés depuis Euclide . L'année 1872 a vu la publication des théories de Karl Weierstrass (par son élève Kossak), Heine ( Crelle, 74), Georg Cantor (Annalen, 5), et Richard Dedekind. Méray avait pris en 1869 le même point de départ que Heine, mais la théorie est généralement appelé à l'année 1872. La méthode de Weierstrass a été complètement énoncée par Salvatore Pincherle en 1880, et a reçu de Dedekind importance supplémentaire par le travail de l'auteur plus tard (1888) et l'approbation récente par Paul Tannery (1894). Weierstrass, Cantor et Heine fondent leurs théories sur la série infinie, alors que Dedekind fonde son sur l'idée d'un couper (Schnitt) dans le système des nombres réels , en séparant tous les nombres rationnels en deux groupes ayant certaines propriétés caractéristiques. Le sujet a reçu des contributions ultérieures aux mains de Weierstrass, Kronecker (Crelle, 101), et Méray.

Fractions continues, étroitement liés à des nombres irrationnels (et en raison de Cataldi, 1613), ont reçu une attention aux mains de Euler , et à l'ouverture de la dix-neuvième siècle ont été mis en évidence à travers les écrits de Lagrange . Dirichlet également ajouté à la théorie générale, de même que de nombreux contributeurs aux applications de l'objet.

Lambert se est avéré (1761) que π ne peut pas être rationnelle, et que e ⁿ est irrationnel si n est rationnel (sauf n = 0). Bien que la preuve de Lambert est souvent dite incomplète, évaluations modernes prennent en charge comme satisfaisante, et en fait pour son temps inhabituellement rigoureux. Legendre (1794), après l'introduction du Fonction de Bessel-Clifford, fourni une preuve pour montrer que π ² est irrationnel, où il suit immédiatement que π est irrationnel aussi. L'existence de nombres transcendants premier a été créé par Liouville (1844, 1851). Plus tard, Georg Cantor (1873) a prouvé leur existence par une méthode différente, qui a montré que chaque intervalle dans les reals contient des nombres transcendants. Charles Hermite (1873) d'abord prouvé transcendantale, et Ferdinand von Lindemann (1882), à partir des conclusions de Hermite, a montré le même pour π. La preuve de Lindemann a été beaucoup simplifiée par Weierstrass (1885), encore par David Hilbert (1893), et a finalement été rendu élémentaire par Adolf Hurwitz et Paul Albert Gordan.

Exemple preuves

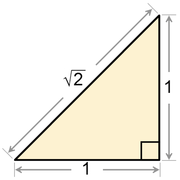
La racine carrée de 2

L'irrationalité de la racine carrée de 2 peut être prouvée en supposant qu'il est rationnel et d'en déduire une contradiction, un argument appelé par reductio ad absurdum. L'argument suivant fait appel à deux reprises sur le fait que le carré d'un nombre impair est toujours impair.

Si √ 2 est rationnel, il a la forme m / n pour des entiers m, n, même pas les deux. Puis m ² = 2 n ² où m est encore, dit m = 2 p. Ainsi 4 p ² = 2 n ² donc 2 p ² = n ² où n est également même, une contradiction.

Une autre preuve

Ce qui suit reductio argument ad absurdum est moins bien connu. Il utilise les informations supplémentaires √2> 1.

1. Supposons que √2 est un nombre rationnel. Cela signifie qu'il existe des entiers m et n avec n ≠ 0 tel que m / n = √2.
2. Puis √2 peut également être écrit comme une fraction irréductible m / n avec des nombres entiers positifs, parce √2> 0.
3. Puis 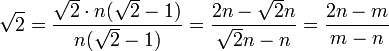, Parce .
4. Depuis √2> 1, il se ensuit que m> n, qui à son tour implique que m> 2 n - m.
5. Ainsi, la fraction m / n pour √2, qui selon le point (2) est déjà en termes plus bas, est représenté par (3) en termes strictement inférieurs. Ce est une contradiction, donc l'hypothèse que √2 est rationnel doit être fausse.

De même, assumer un triangle isocèle dont la jambe droite et hypoténuse avoir des longueurs n et m entiers respectifs. Par le théorème de Pythagore , le rapport m / n est égal à √2. Il est possible de construire par un classique règle et au compas construction un triangle rectangle isocèle petits dont la jambe et l'hypoténuse ont des longueurs respectives m - n et 2 n - m. Que la construction se avère l'irrationalité de √2 par le genre de méthode qui a été employée par les anciens géomètres grecs.

La racine carrée de 10 et au-delà

Si √ 10 est rationnel, dire m / n, m ² = 10 n ^2. Cependant, en notation décimale, chaque carré se termine par un nombre pair de zéros. Alors m ² et 10 n ² en décimal doit se terminer par respectivement un nombre pair et impair de zéros, une contradiction.

Plus généralement, dans ne importe quel r radix qui ne est pas lui-même un carré, chaque carré se termine par un même nombre de zéros, où √ 10 _r en base r est irrationnel, ce est-à √ r est irrationnel. Il se ensuit que les seuls entiers avec racines carrées rationnelles sont des carrés. Comme un cas au point, 2 ne est pas un carré, et 2 en binaire est 10 _2. (Notez la convention de subscripting chiffres non décimal avec leur base, pour éviter toute ambiguïté. Dans le cadre de cette convention, les indices sont compris comme en décimal, ne étant pas eux-mêmes en indice.)

Pour aller plus loin, nous pouvons considérer m ^k = r × n ^k pour tout entiers r et k. Si r ≠ u ^k pour tout entier u, alors R a au moins un facteur premier p élevée à un exposant qui ne est pas divisible par k. Comme tous les exposants dans le Premier factorisation de m ^k sont divisibles par k, pour l'équation de tenir, la factorisation de n ^k doit contenir p élevé à une puissance qui ne est pas non divisible par k. Mais ce est clairement impossible. Ainsi, pour tout entiers r et ^k, k √ r est irrationnel si r ≠ u ^k pour tout entier u. Ce résultat découle également du fait que soulever un nombre rationnel non entier d'une puissance entière ne peut jamais égaler un nombre entier plus une.

Le nombre d'or

Quand un segment de droite est divisé en deux sous-segments disjoints de telle sorte que le rapport de l'ensemble de la partie la plus longue est égal au rapport de la partie la plus longue de la partie la plus courte, alors que le ratio est le nombre d'or , égal à

Supposons que ce est un nombre rationnel n / m en termes plus bas. N Prendre comme la longueur de l'ensemble et m la longueur de la partie plus longue. Ensuite, n> m, et la longueur de la partie plus courte est le N - m. Ensuite, nous avons

Toutefois, cela met une fraction déjà en termes plus bas dans la contradiction de termes inférieurs. Par conséquent, l'hypothèse initiale, que le nombre d'or est rationnel, est fausse.

Logarithmes

Peut-être les numéros les plus faciles à prouver pour être irrationnelle sont certains logarithmes . Voici une preuve par reductio ad absurdum qui se connectent ₂ 3 est irrationnelle:

• Présumer que log ₂ 3 est rationnel. Pour certains entiers positifs m et n, nous avons log ₂ = 3 m / n.
• Il en résulte que 2 ^{m / n} = 3.
• Soulevez chaque côté à l'n puissance, trouvez 2 ^m = 3 ^n.
• Mais 2 à une puissance entière supérieure à 0 est pair (car au moins l'un de ses facteurs premiers est égal à 2) et 3 à une puissance entière plus grande que 0 est impair (parce qu'aucun de ses facteurs premiers est égal à 2), de sorte que l'hypothèse de départ est fausse.

Des cas comme log ₁₀ 2 peuvent être traités de manière similaire.

Irrationnels et algébriques transcendantales

Presque tous les nombres irrationnels sont transcendantale et tout nombres transcendants sont irrationnelles: l'article sur nombres transcendants énumère plusieurs exemples e ^r et π ^r sont irrationnelles si r ≠ 0 est rationnel; e ^π est aussi irrationnel..

Une autre façon de construire des nombres irrationnels est aussi irrationnel nombres algébriques, ce est à dire sous forme de zéros de polynômes à coefficients entiers: commencent par une équation polynomiale

p (x) = a _n x ⁿ + a _n-1 x ^n-1 + ... + a ₁ x + a ₀ = 0

où les coefficients a _i sont des nombres entiers. Supposons que vous savez qu'il existe un nombre réel x avec p (x) = 0 (par exemple si n est impair et un _n est non nul, en raison de la théorème de la valeur intermédiaire). Les seules racines rationnelles possibles de cette équation polynomiale sont de la forme R / s où R est un diviseur de ₀ et s est un diviseur de _n; il ya seulement un nombre fini de ces candidats que vous pouvez tout chèque à la main. Si aucun d'eux ne est une racine de p, alors x doit être irrationnel. Par exemple, cette technique peut être utilisée pour montrer que x = (2 ^1/2 + 1) ^1/3 est irrationnel: nous avons (x ^{3-1) 2} = 2 et donc x ^6-2 x ^3-1 = 0 et ce dernier polynôme n'a pas de racines rationnelles (les seuls candidats pour vérifier sont ± 1).

Du fait que les nombres algébriques forment un domaine, de nombreuses nombres irrationnels peut être construit en combinant des nombres transcendants et algébriques. Par exemple 3π + 2, + π √ √ 2 et e 3 sont irrationnelles (et même transcendantale).

Expansions décimales

L'expansion décimale d'un nombre irrationnel ne se répète jamais ou se termine, contrairement à un nombre rationnel.

Pour le montrer, supposons que nous diviser des nombres entiers n par m (où m est non nul). Quand division longue est appliquée à la division du n par m, m seulement restes sont possibles. Si 0 apparaît comme un reste, le développement décimal se termine. Si 0 ne se produit jamais, alors l'algorithme peut fonctionner au plus m - 1 étapes sans utiliser reste plus d'une fois. Après cela, un reste doit se reproduire, puis les répétitions d'expansion décimales!

Inversement, supposons que nous sommes confrontés à un récurrente décimal, nous pouvons prouver que ce est une fraction de deux nombres entiers. Par exemple:

Ici la longueur de la repitend est 3. On multiplie par ³ 10:

Notez que, depuis, nous avons multiplié par 10 à la puissance de la longueur de la partie à répéter, nous avons réorienté les chiffres à gauche de la virgule exactement que de nombreux postes. Par conséquent, l'extrémité de queue de 1000 A correspond à l'extrémité de queue de A exactement. Ici, à la fois A et 1000 A 162 ont répéter à la fin.

Par conséquent, lorsque l'on soustrait une des deux parties, l'extrémité de queue de 1000 A annule hors de l'extrémité de queue de A:

Puis

qui est un quotient d'entiers et donc un nombre rationnel.

Questions ouvertes

On ne sait pas si π + π ou e - e est irrationnel ou non. En fait, il n'y a pas de paire de nombres entiers non nuls m et n pour laquelle il est connu que m + π ne est irrationnel ou non. En outre, on ne sait pas si l'ensemble {π, e} est algébriquement indépendants sur Q.

On ne sait pas si les deux ^e, π ^e, π ^√2, Constante de Catalan, ou Euler-Mascheroni Gamma γ constants sont irrationnelles.

L'ensemble des irrationnels

Depuis les réels forment un ensemble non dénombrable dont les rationnels sont un sous-ensemble dénombrable, l'ensemble complémentaire de irrationnels est incalculable.

Sous l'habitude ( Euclidienne) fonction de distance d (x, y) = | x - y |, les chiffres réels sont un espace métrique et donc aussi un espace topologique. Restriction de la fonction de distance euclidienne donne les irrationnels la structure d'un espace métrique. Étant donné que le sous-espace de irrationnels ne est pas fermé, la métrique induite ne est pas complet. Cependant, étant un G-delta ensemble - ce est à dire, une intersection dénombrable de parties ouvertes - dans un espace métrique complet, l'espace des irrationnels est topologiquement complète: ce est, il est une métrique sur les irrationnels induisant la même topologie que la restriction de la métrique euclidienne, mais à l'égard desquels les irrationnels sont complets. On peut voir cela sans savoir le fait mentionné ci-dessus sur les jeux de G-delta: le développement en fraction continue d'un nombre irrationnel définit un homéomorphisme de l'espace des irrationnels à l'espace de toutes les séquences de nombres entiers positifs, qui est facilement visibles pour être complètement métrisable.

En outre, l'ensemble de tous irrationnels est un espace métrique déconnecté.