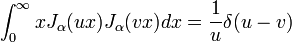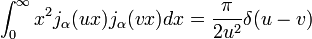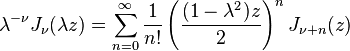Fonction de Bessel
Saviez-vous ...
Cette sélection écoles a été choisi par SOS Enfants pour les écoles dans le monde en développement ne ont pas accès à Internet. Il est disponible en téléchargement intranet. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
En mathématiques , les fonctions de Bessel, d'abord définis par le mathématicien Daniel Bernoulli et généralisée par Friedrich Bessel, sont solutions canonique y (x) de Bessel de l'équation différentielle :
pour une quelconque nombre réel ou complexe α. Le cas particulier le plus commun et important est l'endroit où α est un entier n, alors α est appelé l'ordre de la fonction de Bessel.
Bien que α et -α produire la même équation différentielle, il est classique de définir des fonctions de Bessel de ces deux commandes (par exemple, de sorte que les fonctions sont des fonctions de Bessel essentiellement lisses de α). Fonctions de Bessel sont également connus comme les fonctions cylindre ou harmoniques cylindriques parce qu'ils se trouvent dans la solution à L'équation de Laplace dans Les coordonnées cylindriques.
Applications
L'équation de Bessel se pose lorsque la recherche de solutions à séparables L'équation de Laplace et le Équation de Helmholtz à cylindrique ou coordonnées sphériques . Fonctions de Bessel sont donc particulièrement important pour de nombreux problèmes de la propagation des ondes, les potentiels statiques, et ainsi de suite. Dans la résolution des problèmes dans les systèmes de coordonnées cylindrique, on obtient les fonctions de Bessel d'ordre entier (de α = n); des problèmes sphériques, on obtient des commandes demi-entiers (α = n + ½). Par exemple:
- des ondes électromagnétiques dans un cylindrique guide d'ondes
- la conduction de la chaleur dans un objet cylindrique.
- modes de vibration d'une circulaire mince (ou annulaire) membrane artificielle.
- problèmes de diffusion sur un réseau.
Fonctions de Bessel ont également des propriétés utiles pour d'autres problèmes, tels que le traitement de signal (par exemple, voir La synthèse FM, Fenêtre de Kaiser, ou Filtre de Bessel).
Définitions
Puisque ce est une équation différentielle du second ordre, il doit y avoir deux solutions linéairement indépendantes. Selon les circonstances, cependant, différentes formulations de ces solutions sont pratiques, et les différentes variantes sont décrites ci-dessous.
Fonctions de Bessel du premier type: 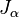
Fonctions de Bessel de la première espèce, noté J α (x), sont des solutions de l'équation différentielle de Bessel qui sont finis à l'origine (x = 0) pour entiers non-négatifs α et divergent x tend vers zéro pour les non-entier négatif α. Le type de solution (par exemple, nombre entier ou non entier) et la normalisation de J α (x) sont définis par les propriétés ci-dessous. Pour les solutions d'ordre entier, il est possible de définir la fonction en sa série de Taylor autour d'extension x = 0:
où  est le fonction gamma, une généralisation de la factorielle fonction pour des valeurs non entières. Pour non entier α, un plus générale série de puissance agrandissement est nécessaire. Les graphiques des fonctions de Bessel regardent à peu près comme oscillant fonctions sinus ou cosinus qui se désintègrent proportionnellement à 1 / √ x (voir aussi leurs formes asymptotiques ci-dessous), bien que leurs racines ne sont généralement pas périodique, sauf pour les grandes asymptotiquement x. (La série de Taylor indique que
est le fonction gamma, une généralisation de la factorielle fonction pour des valeurs non entières. Pour non entier α, un plus générale série de puissance agrandissement est nécessaire. Les graphiques des fonctions de Bessel regardent à peu près comme oscillant fonctions sinus ou cosinus qui se désintègrent proportionnellement à 1 / √ x (voir aussi leurs formes asymptotiques ci-dessous), bien que leurs racines ne sont généralement pas périodique, sauf pour les grandes asymptotiquement x. (La série de Taylor indique que  est la dérivée de
est la dérivée de 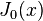 , Un peu comme
, Un peu comme 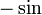 est la dérivée de
est la dérivée de  ; plus généralement, le dérivé de
; plus généralement, le dérivé de 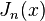 peut être exprimée en termes de
peut être exprimée en termes de  par les identités ci-dessous ).
par les identités ci-dessous ).

Pour les non-entiers α, les fonctions  et
et 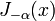 sont linéairement indépendants, et sont donc les deux solutions de l'équation différentielle. D'autre part, pour l'ordre entier
sont linéairement indépendants, et sont donc les deux solutions de l'équation différentielle. D'autre part, pour l'ordre entier  , La relation suivante est valable:
, La relation suivante est valable:
Cela signifie que les deux solutions ne sont linéairement indépendants. Dans ce cas, la deuxième solution linéairement indépendante est ensuite révélée être la fonction de Bessel de la seconde espèce, comme on le verra ci-dessous.
Les intégrales de Bessel
Une autre définition de la fonction de Bessel, pour des valeurs entières de 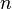 , Est possible en utilisant une représentation intégrale:
, Est possible en utilisant une représentation intégrale:
Ce est l'approche que Bessel utilisé, et à partir de cette définition qu'il tirait plusieurs propriétés de la fonction.
Une autre représentation intégrale est:
Relation à la série hypergéométrique
Les fonctions de Bessel peuvent être exprimées en termes de séries hypergéométriques que
Cette expression est en relation avec le développement de fonctions de Bessel en termes de Fonction de Bessel-Clifford.
Fonctions de Bessel de deuxième type: 
Les fonctions de Bessel de deuxième type, désignés par Y α (x), sont des solutions de l'équation différentielle de Bessel. Ils sont singuliers ( infinie) à l'origine (x = 0).

Y α (x) est parfois aussi appelé la fonction Neumann, et est occasionnellement noté la place de N α (x). Pour non entiers α, elle est liée à J α (x) par:
Dans le cas de l'ordre n nombre entier, la fonction est définie en prenant la limite comme un non entier α tend à n ':
qui a pour conséquence (sous forme intégrale)
Pour le cas de non-entiers α, la définition de Y α (x) est redondant (comme il ressort de la définition ci-dessus). D'autre part, lorsque α est un nombre entier, Y α (x) est la deuxième solution linéairement indépendantes de l'équation de Bessel; De plus, comme ce était le cas est similaire pour les fonctions de la première sorte, la relation suivante est valable:
Les deux J α (x) et Y α (x) sont fonctions holomorphes de x sur le plan complexe coupés le long de l'axe réel négatif. Quand α est un nombre entier, il ne est pas point de ramification, et les fonctions de Bessel sont fonctions entières de x. Si x est maintenu fixe, puis les fonctions de Bessel sont des fonctions entières de α.
Fonctions de Hankel: 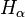
Une autre formulation important des deux solutions linéairement indépendantes de l'équation de Bessel sont les fonctions de Hankel H α (1) (x) α et H (2) (x), définies par:
où i est l' unité imaginaire . Ces combinaisons linéaires sont également connus comme les fonctions de Bessel du troisième type; ils sont deux solutions linéairement indépendantes de l'équation différentielle de Bessel. Les fonctions de Hankel du premier et du second type sont utilisés pour exprimer vers l'extérieur et vers l'intérieur se propageant solutions d'ondes cylindrique de l'équation d'onde cylindrique, respectivement (ou vice versa, en fonction de la convention de signe pour le fréquence). Ils sont nommés d'après Hermann Hankel.
En utilisant les relations précédentes, ils peuvent se exprimer ainsi:
si α est un nombre entier, la limite doit être calculée. Les relations suivantes sont valides, si α est un nombre entier ou non:
Fonctions de Bessel modifiées: 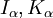
Les fonctions de Bessel sont valables même pour complexes arguments x, et un cas particulier important est celui d'un argument purement imaginaire. Dans ce cas, les solutions de l'équation de Bessel sont appelés les fonctions de Bessel modifiées (ou parfois les fonctions de Bessel hyperboliques) du premier et du deuxième type, et sont définies par:
Ceux-ci sont choisis pour être de valeur réelle pour les arguments réels x. Le développement en série de I α (x) est donc analogue à celle J α (x), mais sans l'alternance (-1) Facteur de m.
Je α (x) et K α (x) sont les deux solutions linéairement indépendantes de l'équation de Bessel modifiée:
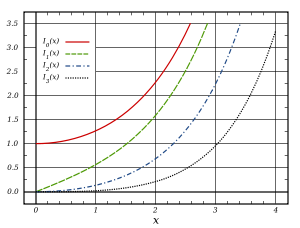
Contrairement aux fonctions de Bessel ordinaires, qui sont oscillant fonctions d'un véritable argument, je α et K α sont en croissance exponentielle et fonctions en décomposition, respectivement. Comme l'ordinaire la fonction de Bessel J α, la fonction I α tend vers zéro à x = 0 pour α> 0 et est fini en x = 0 pour α = 0. De manière analogue, K α diverge en x = 0.
 |  |
La fonction de Bessel modifiée de deuxième espèce a également été appelé par les noms maintenant rares:
- Fonction Basset
- fonction de Bessel modifiée du troisième type
- Fonction MacDonald
Sphériques fonctions de Bessel: 


Lorsque la résolution du Équation de Helmholtz en coordonnées sphériques par séparation des variables, l'équation radiale a la forme:
Les deux solutions linéairement indépendantes de cette équation sont appelés les fonctions de Bessel sphérique j n et y n, et sont liés à l'ordinaire fonctions de Bessel J n et Y n par:
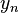 est également notée
est également notée 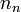 ou η n; certains auteurs appellent ces fonctions les fonctions sphériques Neumann.
ou η n; certains auteurs appellent ces fonctions les fonctions sphériques Neumann.
Les fonctions de Bessel sphériques peuvent également se écrire:
La première fonction de Bessel sphérique  est également connue sous le nom (non normalisée) fonction sinc. Les premières fonctions de Bessel sphériques sont:
est également connue sous le nom (non normalisée) fonction sinc. Les premières fonctions de Bessel sphériques sont:
et
Il ya aussi des analogues sphériques des fonctions de Hankel:
En fait, il ya des simples expressions forme fermée pour les fonctions de Bessel de Afin demi-entier en termes de la norme fonctions trigonométriques , et donc pour les fonctions de Bessel sphériques. En particulier, pour les entiers non-négatifs n:
et h n (2) est le complexe conjugué de la présente (par réel x). Il en résulte, par exemple, que j 0 (x) = sin (x) / x 0 et y (x) = cos (x) / x, et ainsi de suite.
Fonctions Riccati-Bessel: 
Fonctions de Riccati-Bessel diffèrent que légèrement des fonctions de Bessel sphériques:
Ils satisfont l'équation différentielle:
Cette équation différentielle, et les solutions de Riccati-Bessel, se pose dans le problème de la diffusion des ondes électromagnétiques par une sphère, connu sous le nom Diffusion de Mie après la première solution publiée par Mie (1908). Voir, par exemple Du (2004) pour les développements récents et les références.
Suivant Debye (1909), la notation  est parfois utilisé à la place de
est parfois utilisé à la place de  .
.
Formes asymptotiques
Les fonctions de Bessel sont les suivantes formes asymptotiques pour α non-négative. Pour les petits arguments  , On obtient:
, On obtient:
où γ est le Euler-Mascheroni constant (0,5772 ...) et Γ désigne la fonction gamma. Pour les grands arguments 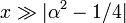 , Ils deviennent:
, Ils deviennent:
(Pour α = 1/2 ces formules sont exactes, voir les fonctions de Bessel sphériques ci-dessus.) Formes asymptotique pour les autres types de fonction de Bessel suivent carrément des relations ci-dessus. Par exemple, pour les grands 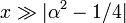 , Les fonctions de Bessel modifiées deviennent:
, Les fonctions de Bessel modifiées deviennent:
tandis que pour les petits arguments  , Ils deviennent:
, Ils deviennent:
Propriétés
Pour entier afin α = n, J n est souvent définie par un Laurent série pour une fonction de génération:
une approche utilisée par PA Hansen en 1843. (Ceci peut être généralisé à l'ordre non entier par l'intégration de contour ou d'autres méthodes.) Un autre relation importante pour les commandes entières est le Jacobi-Anger identité:
qui est utilisé pour étendre un onde plane comme une somme d'ondes cylindriques, ou pour trouver le série de Fourier d'une tonalité modulée Le signal FM.
Les fonctions α J, Y, H α α (1), et H α (2) satisfaire à toutes les relations de récurrence:
où Z désigne J, Y, H (1), ou H (2). (Ces deux identités sont souvent combinés, par exemple ajouté ou soustrait, pour obtenir divers autres relations.) De cette façon, par exemple, on peut calculer les fonctions de Bessel de commandes plus élevés (ou des dérivés plus élevés) étant donné les valeurs en ordres inférieurs (ou dérivés inférieurs ). En particulier, il se ensuit que:
Fonctions de Bessel modifiées suivent relations similaires:
et
La relation de récurrence lit
C où α dénote je α ou e απ i K α. Ces relations de récurrence sont utiles pour les problèmes de diffusion discrets.
Parce que l'équation de Bessel devient Hermitienne (auto-adjoint) se il est divisé par x, les solutions doivent satisfaire une relation d'orthogonalité des conditions aux limites appropriées. En particulier, il se ensuit que:
où α> 1, δ m, n est le Kronecker delta, et u α, m est la m ième de zéro J α (x). Cette relation d'orthogonalité peut ensuite être utilisé pour extraire les coefficients de la Série de Fourier-Bessel, où une fonction est détendu dans la base des fonctions J α (x u α, α m) pour fixe et variable m. (Une relation analogue pour les fonctions de Bessel sphériques suit immédiatement.)
Une autre relation d'orthogonalité est l'équation de fermeture:
pour α> -1/2 et où δ est la Fonction de Dirac. Cette propriété est utilisée pour construire une fonction arbitraire parmi une série de fonctions de Bessel au moyen de la Transformée de Hankel. Pour les fonctions de Bessel sphériques la relation d'orthogonalité est:
pour α> 0.
Une autre propriété importante des équations de Bessel, qui découle de L'identité d'Abel, implique la Wronskien des solutions:
où A et B α α sont toutes deux des solutions de l'équation de Bessel et C α est une constante indépendante de x (qui dépend de α, et sur les fonctions particulières de Bessel considérés). Par exemple, si A = α J α et α B = Y α, α est alors C 2 / π. Cela vaut également pour les fonctions de Bessel modifiées; par exemple, si A = α I et α B α = K α, α est alors C -1.
(Il ya un grand nombre d'autres intégrales et des identités connues qui ne sont pas reproduites ici, mais qui peuvent être trouvés dans les références.)
Multiplication théorème
Les fonctions de Bessel obéissent à une multiplication théorème
où  et
et 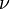 peuvent être pris comme des nombres complexes quelconques. Une forme similaire peut être accordé pour
peuvent être pris comme des nombres complexes quelconques. Une forme similaire peut être accordé pour  et etc. Voir
et etc. Voir

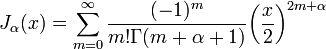



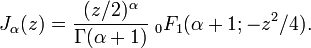
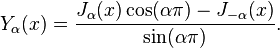
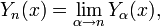
![Y_n (x) = \ frac {1} {\ pi} \ int_ {0} ^ {\ pi} \ sin (x \ sin \ theta - n \ theta) d \ theta - \ frac {1} {\ pi} \ int_ {0} ^ {\ infty} \ left [e ^ {nt} + (-1) ^ ne ^ {- nt} \ right] e ^ {- x \ sinh t} dt.](../../images/208/20863.png)




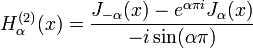
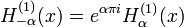
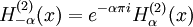
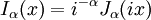


![x ^ 2 \ frac {d ^ 2 y} {dx} ^ 2 + 2x \ frac {} {dx dy} + [x ^ 2 - n (n + 1)] y = 0.](../../images/209/20907.png)
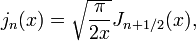





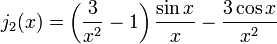

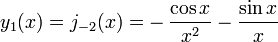


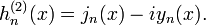



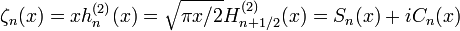
![x ^ 2 \ frac {d ^ y} 2 {^ 2} dx + [x ^ 2 - n (n + 1)] y = 0](../../images/209/20927.png)

![Y_ \ alpha (x) \ rightarrow \ gauche \ {\ begin {matrix} \ frac {2} {\ pi} \ left [\ ln (x / 2) + \ gamma \ right] et \ mbox {if} \ alpha = 0 \\ \\ - \ frac {\ Gamma (\ alpha)} {\ pi} \ left (\ frac {2} {x} \ right) ^ \ alpha et \ mbox {if} \ alpha> 0 \ end {matrix} \ right.](../../images/209/20932.png)
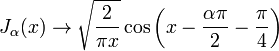






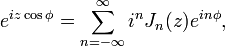

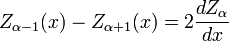
![\ Left (\ frac {d} {x dx} \ right) ^ m \ left [x ^ \ alpha Z _ {\ alpha} (x) \ right] = x ^ {\ alpha - m} Z _ {\ alpha - m } (x)](../../images/209/20944.png)
![\ Left (\ frac {d} {x} dx \ right) ^ m \ left [\ frac {Z_ \ alpha (x)} {x ^ \ alpha} \ right] = (-1) ^ m \ frac {Z_ {\ alpha} + m (x)} {x ^ {\ alpha + m}}](../../images/209/20945.png)


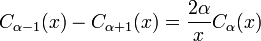

![\ Int_0 ^ 1 x J_ \ alpha (x u _ {\ alpha, m}) J_ \ alpha (x u _ {\ alpha, n}) dx = \ frac {\ delta_ {m, n}} {2} [J_ { \ alpha + 1} (u _ {\ alpha, m})] ^ 2 = \ frac {\ delta_ {m, n}} {2} [J _ {\ alpha} '(u _ {\ alpha, m})] ^ 2,](../../images/209/20950.png)