
Variance
Contexte des écoles Wikipédia
Cette sélection de wikipedia a été choisi par des bénévoles aidant les enfants SOS de Wikipedia pour cette sélection Wikipedia pour les écoles. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille près de la charité. Lire la suite ...
Dans la théorie des probabilités et des statistiques , la variance d'une variable aléatoire , distribution de probabilité , ou l'échantillon est une mesure de dispersion statistique, la moyenne de la distance au carré des valeurs possibles de la valeur attendue (moyenne). Alors que la moyenne est une façon de décrire l'emplacement d'une distribution, la variance est un moyen de capturer son ampleur ou le degré de se étalant. Le unité de la variance est le carré de l'unité de la variable d'origine. La racine carrée de la variance, appelée écart-type , a les mêmes unités que la variable d'origine et peut être plus facile à interpréter pour cette raison.
La variance d'une vraie variable aléatoire -Évaluées est sa deuxième moment central, et il arrive aussi d'être sa deuxième cumulant. Tout comme certaines distributions ne ont pas une moyenne, certains ne ont pas un écart aussi bien. La moyenne existe chaque fois la variance existe, mais pas vice versa.
Définition
Si μ = E (X) est le valeur attendue (moyenne) de la variable aléatoire X, la variance est
Cette définition englobe les variables aléatoires qui sont discrète , continue , ou aucun des deux. De tous les points sur lesquels les écarts au carré aurait pu être calculées, la moyenne produit la valeur minimale pour la somme moyenne des carrés des écarts.
De nombreuses distributions, tels que la Distribution de Cauchy, ne ont pas un écart parce que les intégrale diverge pertinents. En particulier, si la distribution ne est pas une valeur attendue, il n'a pas non plus une variance. L'inverse ne est pas vrai: il ya des distributions pour lesquelles la valeur attendue existe, mais la variance ne est pas.
Cas discret
Si la variable aléatoire est discrète avec probabilité fonction de masse de p 1, ..., p n, ce qui équivaut à
(Note: cette variation doit être divisée par la somme des poids dans le cas d'une discrète variance pondérée.) Ce est, ce est la valeur attendue de la carré de l'écart de X à partir de sa propre moyenne. En clair, il peut être exprimé comme «La moyenne du carré de la distance de chaque point de la moyenne des données". Ce est donc la déviation quadratique moyenne. La variance de variable aléatoire X est généralement désigné comme Var (X), 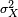 , Ou tout simplement σ 2.
, Ou tout simplement σ 2.
Propriétés
La variance est non-négatif, car les places sont positives ou nulles. La variance d'une variable aléatoire est égal à 0 si et seulement si la variable est dégénérée, ce est à dire qu'il prend une valeur constante avec une probabilité de 1, et la variance d'une variable dans un ensemble de données est 0 si et seulement si toutes les entrées ont le même valeur.
La variance est invariante par rapport aux changements dans un paramètre de position. Autrement dit, si une constante est ajoutée à l'ensemble des valeurs de la variable, la variance est inchangé. Si toutes les valeurs sont mises à l'échelle par une constante, la variance est réduite par le carré de cette constante. Ces deux propriétés peuvent être exprimées dans la formule suivante:
La variance d'une somme finie de variables aléatoires non corrélées est égale à la somme de leurs variances.
- Supposons que les observations peuvent être divisées en sous-groupes selon certains seconde variable. Ensuite, la variance de l'ensemble du groupe est égal à la moyenne des variances des sous-groupes ainsi que la variance de la moyenne des sous-groupes. Cette propriété est connue sous le nom décomposition de la variance ou la droit de la variance totale et joue un rôle important dans la analyse de la variance. Par exemple, supposons qu'un groupe se compose d'un sous-groupe d'hommes et un aussi grand sous-groupe de femmes. Supposons que les hommes ont une longueur moyenne de corps 180 et que la variance de leurs longueurs est de 100. Supposons que les femmes ont une longueur moyenne de 160 et que la variance de leurs longueurs est de 50. Ensuite, la moyenne des variances est (100 + 50) / 2 = 75; la variance des moyens est la variance de 180, 160 qui est de 100. Ensuite, pour l'ensemble du groupe des hommes et femmes confondus, la variance des longueurs de corps sera 75 + 100 = 175. Notez que cette utilise N pour le dénominateur au lieu de N - 1.
Dans un cas plus général, si les sous-groupes ont des tailles inégales, alors ils doivent être pondérés proportionnellement à leur taille dans les calculs des moyennes et des variances. La formule est valable également avec plus de deux groupes, et même si la variable de regroupement est continue.
Cette formule implique que la variance de l'ensemble du groupe ne peut pas être plus petit que la moyenne des variances des sous-groupes. Notez, cependant, que la variance totale ne est pas nécessairement plus grande que les variances des sous-groupes. Dans l'exemple ci-dessus, lorsque les sous-groupes sont analysés séparément, la variance est influencée seulement par les différences homme-homme et les différences femme-femme. Si les deux groupes sont combinées, cependant, les différences hommes-femmes entrent dans la variance aussi.
- De nombreuses formules de calcul pour la variance sont basées sur cette égalité:. L'écart est égal à la moyenne des carrés moins le carré de la moyenne Par exemple, si l'on considère les chiffres 1, 2, 3, 4 alors la moyenne des carrés est (1 + 1 × 2 × 2 × 3 + 3 + 4 x 4) / 4 = 7,5. La moyenne est de 2,5, de sorte que le carré de la moyenne est de 6,25. Par conséquent, la variance est 07/05 au 06/25 = 1,25, ce qui est bien le même résultat obtenu plus tôt avec les formules de définition. Beaucoup de calculatrices de poche utilisent un algorithme qui est basé sur la formule et qui leur permet de calculer la variance pendant que les données sont entrées, sans stocker toutes les valeurs en mémoire. L'algorithme consiste à ajuster seulement trois variables lorsqu'une nouvelle valeur de données est entré: Le nombre de données saisies jusqu'à présent (n), la somme des valeurs pour l'instant (S), et la somme des valeurs au carré la mesure (SS) . Par exemple, si les données sont 1, 2, 3, 4, puis après avoir entré la première valeur, l'algorithme faudrait n = 1, S = 1 et SS = 1. Après avoir entré le deuxième valeur (2), il aurait n = 2, 3 et S = SS = 5. Lorsque toutes les données sont saisies, il aurait n = 4, S = 10 et SS = 30. Ensuite, la moyenne est calculée comme M = S / n, et enfin la variance est calculé comme SS / n - M × M. Dans cet exemple, le résultat serait 30/4-2,5 × 2,5 = 7/5 à 6/25 = 1,25. Si l'estimation non biaisée de l'échantillon doit être calculé, le résultat sera multipliée par n / (n - 1), ce qui donne 1,667 dans cet exemple.
Propriétés, formelle
8.a. variance de la somme des variables non corrélées
L'une des raisons pour l'utilisation de la variance de préférence à d'autres mesures de la dispersion, ce est que la variance de la somme (ou la différence) de variables aléatoires non corrélées est la somme de leurs écarts:
Cette déclaration est souvent faite avec la condition plus forte que les variables sont suffit indépendants, mais non corrélation. Donc, si les variables ont la même variance σ 2, puis, depuis division par n est une transformation linéaire, cette formule implique immédiatement que la variance de leur moyenne est
Autrement dit, la variance de la moyenne diminue avec n. Ce fait est utilisé dans la définition de la erreur type de la moyenne d'échantillon, qui est utilisé dans la théorème central limite.
8.b. variance de la somme des variables corrélées
En général, si les variables sont en corrélation, la variance de leur somme est la somme de leur covariances:
Voici Cov est la covariance, qui est nul pour les variables aléatoires indépendantes (si elle existe). La formule indique que la variance de la somme est égale à la somme de tous les éléments de la matrice de covariance des composantes. Cette formule est utilisée dans la théorie de Alpha de Cronbach dans théorie classique des tests.
Donc, si les variables ont variance égale σ 2 et la corrélation moyenne des variables distinctes est ρ, la variance de leur moyenne est
Ceci implique que la variance de la moyenne augmente avec la moyenne des corrélations. En outre, si les variables ont variance unité, par exemple si elles sont normalisés, ce qui simplifie ensuite à
Cette formule est utilisée dans la Spearman-Brown formule de prédiction de la théorie classique des tests. Cette converge vers ρ si n tend vers l'infini, à condition que la corrélation moyenne reste constante ou converge aussi. Ainsi, pour la variance de la moyenne des variables avec des corrélations normalisées égales ou convergent corrélation moyenne, nous avons
Par conséquent, la variance de la moyenne d'un grand nombre de variables normalisées est approximativement égale à leur corrélation moyenne. Il est donc clair que la moyenne de l'échantillon de variables corrélées ne convergent généralement à la moyenne de la population, même si le Loi des grands nombres indique que la moyenne de l'échantillon vont converger pour les variables indépendantes.
8.c. variance d'une somme pondérée de variables
Propriétés 6 et 8, ainsi que cette propriété de la page de covariance: Cov (aX, par) = ab Cov (X, Y) implique conjointement que
Ceci implique que dans une somme pondérée de variables, la variable avec la plus grande aura un poids de manière disproportionnée grand poids de la variance du total. Par exemple, si X et Y ne sont pas corrélées et le poids de X est deux fois le poids de Y, alors le poids de la variance de X sera quatre fois le poids de la variance de Y.
9. La décomposition de variance
La formule générale pour la décomposition de la variance ou la droit de la variance totale est: Si X et Y sont deux variables aléatoires et la variance de X existe,
Ici, E (X | Y) est le espérance conditionnelle de X étant donné Y, et Var (X | Y) est la variance conditionnelle de X sachant Y. (Une explication plus intuitive est que, étant donné une valeur particulière de Y, alors X suit une distribution de moyenne E (X | Y) et la variance Var (X |. Y) La formule ci-dessus indique comment trouver Var (X) sur la base du distributions de ces deux quantités, lorsque Y est autorisé à varier.) Cette formule est souvent appliquée en analyse de la variance, où la formule correspondante est
Il est également utilisé dans la régression linéaire analyse, où la formule correspondante est
Cela peut aussi être dérivé de l'additivité des écarts (propriété 8), depuis le (observé) le score total est la somme du score prédit et le score d'erreur, où les deux derniers ne sont pas corrélés.
10. formule de calcul de la variance
Le formule de calcul de la variance suit d'une manière simple à partir de la linéarité des valeurs attendues et la définition ci-dessus:
Ceci est souvent utilisée pour calculer la variance dans la pratique, même si elle souffre de approximation numérique erreur si les deux composantes de l'équation sont similaires en amplitude.
Propriété caractéristique
Le deuxième moment d'une variable aléatoire atteint la valeur minimum lorsqu'il est pris autour de la moyenne de la variable aléatoire, soit  . Cette propriété pourrait être inversée, ce est à dire si la fonction
. Cette propriété pourrait être inversée, ce est à dire si la fonction  satisfait
satisfait  il est alors nécessaire de la forme
il est alors nécessaire de la forme  . Ce est aussi vrai dans le cas multidimensionnel.
. Ce est aussi vrai dans le cas multidimensionnel.
Approximation de la variance d'une fonction
Le Procédé utilise delta du deuxième ordre développements de Taylor à approximation de la variance d'une fonction d'une ou plusieurs variables aléatoires. Par exemple, la variance approximative d'une fonction d'une variable est donnée par
à condition que f est dérivable deux fois et que la moyenne et la variance de X sont finies.
Généralisations
Si 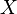 est un vecteur à valeurs variable aléatoire, à valeurs dans
est un vecteur à valeurs variable aléatoire, à valeurs dans 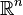 Et considéré comme un vecteur de colonne, puis la généralisation naturelle de la variance est
Et considéré comme un vecteur de colonne, puis la généralisation naturelle de la variance est 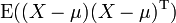 Où
Où 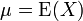 et
et  est la transposée de
est la transposée de 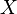 , Et est donc un vecteur ligne. Cet écart est un matrice carrée semi-définie positive, communément dénommé matrice de covariance.
, Et est donc un vecteur ligne. Cet écart est un matrice carrée semi-définie positive, communément dénommé matrice de covariance.
Si 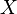 est un complexe variable aléatoire -Évaluées, à valeurs dans
est un complexe variable aléatoire -Évaluées, à valeurs dans 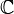 , Puis sa variance est
, Puis sa variance est  Où
Où 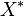 est le conjugué complexe de
est le conjugué complexe de 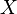 . Cet écart est également une matrice carrée semi-définie positive.
. Cet écart est également une matrice carrée semi-définie positive.
Histoire
Le terme de variance a été introduite par Ronald Fisher dans son document de 1918 La corrélation entre les parents sur la supposition de mendélienne Héritage.
Moment d'inertie
La variance d'une distribution de probabilité est analogue à la moment d'inertie dans la mécanique classique d'une distribution correspondante de masse le long d'une ligne, par rapport à la rotation autour de son centre de masse. Ce est en raison de cette analogie que de telles choses que la variance sont appelés moments de distributions de probabilité . (La matrice de covariance est analogue à la moment d'inertie tenseur pour les distributions multivariées.)
![\ Operatorname {} Var (X) = \ operatorname {} E [(X - \ mu) ^ 2] \,.](../../images/82/8221.png)


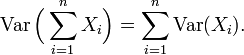
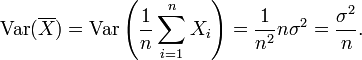


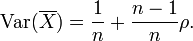

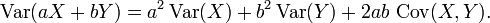



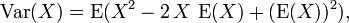


![\ Operatorname {var} \ left [f (X) \ right] \ approx \ gauche (f '(\ operatorname {E} \ left [X \ right]) \ right) ^ 2 \ operatorname {var} \ left [X \ right]](../../images/82/8242.png)
