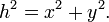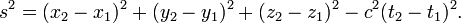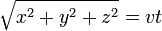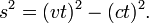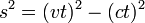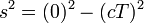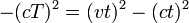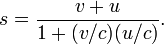Introduction à la relativité restreinte

Albert Einstein lors d'une conférence à Vienne en 1921

Dans la physique , la relativité restreinte est un élément fondamental théorie sur l'espace et le temps , développée par Albert Einstein en 1905 comme une modification de Relativité galiléenne. (Voir " Histoire de la relativité restreinte "pour un compte rendu détaillé et les contributions de Hendrik Lorentz et Henri Poincaré.) La théorie a été en mesure d'expliquer certains pressage théoriques et expérimentales dans les questions de la physique de l'époque impliquant la lumière et électrodynamique, tels que l'échec de la 1887 Expérience de Michelson-Morley, qui visait à mesurer les différences dans la vitesse relative de la lumière due à la La motion de la terre à travers l'hypothétique, et maintenant discrédité, éther luminifère . L'éther a ensuite été considéré comme le milieu de propagation des ondes électromagnétiques comme la lumière.

Einstein a postulé que la vitesse de la lumière dans l'espace libre est la même pour toutes observateurs, indépendamment de leur mouvement par rapport à la source lumineuse, où nous pouvons penser à un observateur comme une entité imaginaire avec un ensemble sophistiqué des appareils de mesure, au repos par rapport à lui-même, qui enregistrent parfaitement les positions et les temps de tous les événements dans l'espace et le temps. Ce postulat découle de l'hypothèse que les équations de Maxwell de l'électromagnétisme , qui prédisent une vitesse spécifique de la lumière dans le vide, détiennent en tout référentiel inertiel plutôt que, comme l'on pensait, juste dans le cadre de l'éther. Cette prédiction contredit les lois de la mécanique classique , qui avaient été acceptés depuis des siècles, en faisant valoir que le temps et l'espace ne sont pas fixes et dans le changement fait pour maintenir une vitesse constante de la lumière indépendamment des mouvements relatifs des sources et des observateurs. L'approche d'Einstein a été basée sur expériences de pensée, les calculs et la principe de relativité, qui est la notion que toutes les lois physiques devraient apparaître même (qui est, prendre la même forme de base) à tous les observateurs inertiels. Aujourd'hui, les scientifiques sont tellement à l'aise avec l'idée que la vitesse de la lumière est toujours le même que le mètre est maintenant défini comme "la longueur du trajet parcouru par la lumière dans le vide pendant un intervalle de temps de 1/299 792 458 de seconde." Cela signifie que la vitesse de la lumière est par convention 299 792 458 m / s (environ 1,079 milliards kilomètres par heure, soit 671 million miles par heure).

Les prédictions de la relativité restreinte sont presque identiques à celles de la relativité galiléenne pour la plupart des phénomènes quotidiens, dans lequel les vitesses sont beaucoup plus bas que la vitesse de la lumière, mais il fait des prédictions différentes, non-évidentes pour les objets se déplaçant à des vitesses très élevées. Ces prédictions ont été testées expérimentalement à de nombreuses reprises depuis la création de la théorie et ont été confirmées par ces expériences. Les principales prédictions de la relativité restreinte sont:

• Relativité de la simultanéité: Les observateurs qui sont en mouvement par rapport à l'autre peuvent être en désaccord sur si deux événements ont eu lieu en même temps ou l'un a eu lieu avant l'autre.
• Dilatation du temps (Un observateur regardant deux horloges identiques, l'un mobile et une au repos, permettra de mesurer l'horloge en mouvement cocher plus lentement)
• La contraction des longueurs (Le long de la direction du mouvement, une tige mobile par rapport à un observateur sera mesuré à être plus courte qu'une tige identique au repos), et
• Le équivalence de la masse et de l'énergie (écrit comme E = mc ^2).

Relativité restreinte prédit une non linéaire formule d'addition de vitesse qui empêche des vitesses supérieures à celle de la lumière d'être observé. En 1908, Hermann Minkowski a reformulé la théorie basée sur différents postulats de nature plus géométrique. Cette approche considère l'espace et le temps comme étant différents composants d'une seule entité, le l'espace-temps, qui est "divisée" de différentes manières par les observateurs en mouvement relatif. De même, l'énergie et l'élan sont les composantes de la quatre élan et l' électrique et champ magnétique sont les composantes de la tenseur électromagnétique.

Comme relativité galiléenne est maintenant considéré comme une approximation de la relativité spéciale valable pour de faibles vitesses, la relativité restreinte est considérée comme une approximation de la théorie de la relativité générale valable pour faible champs gravitationnels. La relativité générale postule que les lois physiques devraient apparaître la même chose pour tous les observateurs (une accélération de cadre de référence étant équivalent à celui dans lequel gravitationnel actes sur le terrain), et que la gravitation est l'effet de la courbure de l'espace-temps causé par l'énergie (y compris la masse).

La physique classique et de l'électromagnétisme

Grâce à l'époque entre Newton et autour du début du 20e siècle, le développement de la physique classique avait fait de grands progrès. La demande de Newton de la loi du carré inverse de la gravité était la clé pour débloquer une grande variété d'événements physiques, de la chaleur de la lumière , et le calcul fait le calcul direct de ces effets traitable. Au fil du temps, de nouvelles techniques mathématiques, notamment le Lagrange, grandement simplifié l'application de ces lois physiques à des problèmes plus complexes.

Comme l'électricité et le magnétisme étaient mieux explorées, il est devenu clair que les deux concepts sont liés. Au fil du temps, ce travail a abouti à des équations de Maxwell , un ensemble de quatre équations qui pourraient être utilisés pour calculer la totalité de l'électromagnétisme. L'un des résultats les plus intéressants de l'application de ces équations était qu'il était possible de construire une onde de champs électriques et magnétiques qui peuvent se propager à travers l'espace autonome. Quand réduit, le calcul a montré que la vitesse de propagation dépendait de deux constantes universelles, et leur rapport est la vitesse de la lumière . Lumière était une onde électromagnétique.

Dans le modèle classique, les vagues sont les déplacements au sein d'un milieu. Dans le cas de la lumière, les vagues ont été pensés pour être déplacements d'un milieu spécial connu sous le nom d'éther luminifère , qui se étendait à travers tout l'espace. Ceci étant le cas, la lumière se déplace dans son propre cadre de référence, le cadre de l'éther. Selon transformer le Galiléen, nous devrions être capables de mesurer la différence de vitesses entre le châssis de l'éther et de tout autre - un cadre universel au dernier.

Concevoir une expérience pour exercer effectivement cette mesure se est avérée très difficile, cependant, que les vitesses et le calendrier impliqués faites mesure précise difficile. Le problème de mesure a finalement été résolu avec le Expérience de Michelson-Morley. À la surprise de tout le monde, pas de mouvement relatif a été vu. Soit l'éther roulait à la même vitesse que la Terre, difficile d'imaginer donné mouvement complexe de la Terre, ou il n'y avait pas éther. Expériences de suivi testé différentes possibilités, et, au début du 20e siècle, elle a été de plus en plus difficile d'échapper à la conclusion que ne existait pas l'éther.

Ces expériences ont montré que tous les lumière n'a tout simplement pas suivre la transformation de Galilée. Et pourtant, il était clair que les objets physiques lumière émise, ce qui conduit à des problèmes non résolus. Si l'on devait réaliser l'expérience sur le train par "éclairer" au lieu de balles, si la lumière ne suit pas la transformation de Galilée, puis les observateurs devraient se entendent pas sur les résultats. Pourtant, il était évident que l'univers était en désaccord; systèmes physiques connus pour être à grande vitesse, comme des étoiles lointaines, avaient la physique qui étaient aussi semblable à la nôtre que les mesures autorisées. Une sorte de transformation devait agir sur la lumière, ou mieux, une seule transformation à la fois la lumière et la matière.

Le développement d'une transformation appropriée pour remplacer la transformation de Galilée est la base de la relativité restreinte.

Invariance de longueur: l'image euclidienne

Le théorème de Pythagore

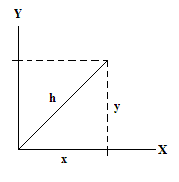
Dans la relativité restreinte, l'espace et le temps sont réunis en un continuum à quatre dimensions unifié appelé l'espace-temps. Pour avoir une idée de ce que l'espace-temps est comme, nous devons d'abord regarder l' espace euclidien de la physique newtonienne classique. Cette approche à expliquer la théorie de la relativité spéciale commence par le concept de " longueur ".

Dans l'expérience quotidienne, il semble que la longueur des objets reste le même, peu importe la façon dont ils sont tournés ou déplacés d'un endroit à l'autre; à la suite de la simple longueur d'un objet ne semble pas changer ou est invariante. Cependant, comme cela est représenté dans les illustrations ci-dessous, ce qui est réellement proposée est que la longueur semble être invariant dans un système de coordonnées à trois dimensions.

La longueur d'une ligne en deux dimensions un système de coordonnées cartésiennes est donnée par le théorème de Pythagore :

L'un des théorèmes de base de l'algèbre vectorielle, ce est que la longueur d'un vecteur ne change pas lorsqu'il est mis en rotation. Cependant, un examen plus approfondi nous dit que ce ne est vrai que si l'on considère rotations confinés au plan. Si nous introduisons la rotation dans la troisième dimension, alors nous pouvons incliner la ligne de l'avion. Dans ce cas, la projection de la ligne sur le plan va se raccourcir. Cela signifie-t les variations de longueur de la ligne? - Évidemment pas. Le monde est en trois dimensions et dans un système de coordonnées cartésiennes 3D la longueur est donnée par la version trois dimensions du théorème de Pythagore:

Ce est invariant par toutes les rotations. La violation apparente de l'invariance de la longueur ne est arrivé parce que nous étions "manque" une dimension. Il semble que, à condition que toutes les directions dans lesquelles un objet peut être incliné ou arrangés sont représentés dans un système de coordonnées, la longueur d'un objet ne change pas sous rotations. Avec le temps et l'espace considéré comme en dehors du domaine de la physique elle-même, en vertu de la mécanique classique un système de coordonnées en 3 dimensions est suffisant pour décrire le monde.

Notez que l'invariance de la longueur ne est pas habituellement considérée comme un principe ou de droit, pas même un théorème. Ce est tout simplement une déclaration sur la nature fondamentale de l'espace lui-même. Espace que nous le concevons habituellement il est appelé en trois dimensions espace euclidien , parce que sa structure géométrique est décrit par les principes de la géométrie euclidienne . La formule pour la distance entre deux points est une propriété fondamentale d'un espace euclidien, il est appelé le tenseur métrique euclidienne (ou simplement la métrique euclidienne). En général, les formules de distance sont appelés tenseurs métriques.

Notez que les rotations sont fondamentalement liés à la notion de longueur. En fait, on peut définir la longueur ou la distance à ce qui reste le même (est invariant) sous rotations, ou de définir des rotations être celle qui garder la longueur invariant. Compte tenu de toute une, il est possible de trouver l'autre. Si nous connaissons la formule de la distance, nous pouvons trouver la formule pour transformer coordonnées dans une rotation. Si, d'autre part, nous avons la formule pour les rotations alors nous pouvons trouver la formule de la distance.

La formulation Minkowski: introduction de l'espace-temps

Après Einstein dérivé relativité restreinte formellement de la (à première vue contre-intuitif) hypothèse que la vitesse de la lumière est la même chose pour tous les observateurs, Hermann Minkowski construit sur des approches mathématiques utilisés dans la géométrie non-euclidienne et sur le travail mathématique de Lorentz et Poincaré. Minkowski a montré en 1908 que la nouvelle théorie d'Einstein pourrait aussi se expliquer par le remplacement de la notion de temps et l'espace séparé avec un continuum à quatre dimensions appelé l'espace-temps. Ce était un concept révolutionnaire, et Roger Penrose a dit que la relativité ne était pas vraiment complète jusqu'à ce Minkowski reformulé les travaux d'Einstein.

Le concept d'un espace à quatre dimensions est difficile à visualiser. Il peut aider au début de penser simplement en termes de coordonnées. Dans l'espace en trois dimensions, il faut trois nombres réels de se référer à un point. Dans le L'espace de Minkowski, on a besoin de quatre nombres réels (trois coordonnées spatiales et une coordonnée de temps) de se référer à un point à un instant particulier de temps. Ce point, spécifié par les quatre coordonnées, se appelle un événement. La distance entre deux événements différents se appelle l'intervalle espace-temps.

Un chemin à travers l'espace-temps à quatre dimensions (généralement connu comme l'espace de Minkowski) est appelé ligne de monde. Comme il indique à la fois la position et l'heure, une particule ayant une ligne de monde connu a une trajectoire complètement déterminé et de la vitesse. Ce est exactement comme graphiquement le déplacement d'une particule se déplaçant en ligne droite contre le temps écoulé. La courbe contient les informations de mouvement complet de la particule.

De la même manière que la mesure de distance dans l'espace 3D besoins, tous les trois coordonnées, il faut comprendre le temps ainsi que les trois coordonnées de l'espace lors du calcul de la distance dans l'espace de Minkowski (ci-après appelé M). Dans un sens, l'intervalle espace-temps fournit une estimation combinée de la distance qui sépare deux événements se produisent dans l'espace ainsi que le temps qui se écoule entre leur occurrence.

Mais il se agit d'un problème; temps est liée aux coordonnées spatiales, mais ils ne sont pas équivalents. Le théorème de Pythagore traite toutes les coordonnées sur un pied d'égalité (voir l'espace euclidien pour plus de détails). Nous pouvons échanger deux coordonnées spatiales sans changer la longueur, mais nous ne pouvons pas simplement échanger un espace de coordonnées avec le temps - ils sont fondamentalement différents. Ce est une chose tout à fait différente pour deux événements à être séparés dans l'espace et d'être séparées dans le temps. Minkowski a proposé que la formule pour la distance avait besoin d'un changement. Il a constaté que la formule correcte est en fait assez simple, ne différant que par un signe du théorème de Pythagore:

où c est une constante et t est le temps de coordonnées. La multiplication par C, qui a la dimensions L T ^-1, convertit le temps en unités de longueur constante, ce qui a la même valeur que la vitesse de la lumière . Donc, l'intervalle de l'espace-temps entre deux événements distincts est donnée par

Il ya deux points importants à noter. Tout d'abord, le temps est mesuré dans les mêmes unités que la longueur en le multipliant par un facteur de conversion constant. Deuxièmement, et plus important encore, le temps coordonnée a un signe différent de celui des coordonnées spatiales. Cela signifie que l'espace-temps dans quatre dimensions, une coordonnée est différent des autres et influe sur la distance différente. Cette nouvelle «distance» peut être nulle, voire négative. Cette nouvelle formule de distance, appelée métrique de l'espace-temps de la, est au cœur de la relativité. Cette formule de distance est appelée tenseur métrique de M. signe Cet moins signifie que beaucoup de notre intuition sur les distances ne peut pas être directement reportée à intervalles d'espace-temps. Par exemple, l'intervalle de l'espace-temps entre deux événements séparés dans le temps et l'espace peut être nulle (voir ci-dessous). A partir de maintenant, la formule termes de distance et tenseur métrique seront utilisés de façon interchangeable, que seront les conditions Minkowski d'intervalle métrique et l'espace-temps.

Dans l'espace-temps de Minkowski l'intervalle espace-temps est la longueur invariant, la longueur de la 3D ordinaire ne est pas tenu d'être invariant. L'intervalle de l'espace-temps doit rester le même dans les rotations, mais longueurs ordinaires peut changer. Tout comme avant, il nous manquait une dimension. Notez que tout est jusqu'à présent uniquement définitions. Nous définissons une construction mathématique à quatre dimensions qui a une formule spéciale pour la distance, où la distance qui reste signifie que les mêmes rotations sous (alternativement, on peut définir une rotation être celle qui maintient la distance inchangé).

Maintenant vient la partie physique. Rotations dans l'espace de Minkowski ont une interprétation différente de rotations ordinaires. Ces rotations correspondent aux transformations de cadre de référence. Le passage d'un cadre de référence à l'autre correspond à la rotation de l'espace de Minkowski. Une justification intuitive en est donnée ci-dessous, mais mathématiquement ce est un postulat dynamique comme en supposant que les lois physiques doivent rester le même sous les transformations de Galilée (qui semble tellement intuitif que nous ne reconnaissons généralement pas être un postulat).

Depuis rotations par définition doit tenir la distance même, de passer à un cadre de référence différent doit garder l'intervalle espace-temps entre deux événements inchangés. Cette exigence peut être utilisé pour dériver une forme mathématique explicite pour la transformation qui doit être appliqué aux lois de la physique (comparer avec l'application de transformations galiléennes aux lois classiques) lors du passage des cadres de référence. Ces transformations sont appelés Transformations de Lorentz. Tout comme le Transformations galiléennes sont l'énoncé mathématique du principe de relativité galiléenne en mécanique classique, les transformations de Lorentz sont la forme mathématique du principe de la relativité d'Einstein. Lois de la physique doivent rester le même sous les transformations de Lorentz. Les équations de Maxwell et L'équation de Dirac satisfaire cette propriété, et donc ils sont relativiste lois correctes (mais classique incorrecte, car ils ne se transforment pas correctement sous les transformations de Galilée).

Avec la déclaration de la métrique de Minkowski, le nom commun pour la formule de la distance indiquée ci-dessus, le fondement théorique de la relativité restreinte est terminée. La base pour l'ensemble de la relativité restreinte peut être résumée par la déclaration géométrique "changements de cadre de référence correspondent à des rotations dans l'espace-temps de Minkowski 4D, qui est défini pour avoir la formule de distance donnée ci-dessus". Les prévisions dynamiques uniques de souches SR de cette propriété géométrique de l'espace-temps. La relativité spéciale peut être dit la physique de l'espace-temps de Minkowski. Dans ce cas, l'espace-temps, il ya six rotations indépendants à prendre en considération. Trois d'entre eux sont les rotations standard sur un plan en deux directions de l'espace. Les trois autres sont des rotations dans un plan à la fois de l'espace et le temps: Ces rotations correspondent à un changement de vitesse , et de la Minkowski diagrammes élaborés par le décrivent ces rotations.

Comme il a été mentionné précédemment, on peut remplacer formules de distance avec des formules de rotation. Au lieu de commencer avec l'invariance de la métrique de Minkowski comme la propriété fondamentale de l'espace-temps, on peut État (comme cela a été fait dans la physique classique avec la relativité galiléenne) la forme mathématique des transformations de Lorentz et exigent que les lois physiques soient invariants par ces transformations. Ce ne fait aucune référence à la géométrie de l'espace-temps, mais va produire le même résultat. Ce était en fait l'approche traditionnelle de SR, utilisé à l'origine par Einstein lui-même. Cependant, cette approche est souvent considéré pour offrir moins de perspicacité et être plus lourdes que le formalisme Minkowski plus naturel.

Le postulat d'Einstein: la constance de la vitesse de la lumière

Le postulat d'Einstein que la vitesse de la lumière est une constante apparaît comme une conséquence naturelle de la formulation Minkowski.

Proposition 1:

Lorsqu'un objet se déplace à c dans un certain cadre de référence, l'intervalle de l'espace-temps est zéro.

Preuve:

L'intervalle de l'espace-temps entre l'origine-événement (0,0,0,0) et un événement (x, y, z, t) est

La distance parcourue par un objet se déplaçant à la vitesse v de t secondes est:

donnant

Depuis la vitesse v égale c nous avons

Ce est pourquoi l'intervalle espace-temps entre les événements de départ et d'arrivée est donnée par

Proposition 2:

Un objet se déplaçant à c dans une trame de référence se déplace à c dans tous les cadres de référence.

Preuve:

Que l'objet se déplacer avec vitesse v quand on l'observe d'un cadre de référence différent. Un changement dans la trame de référence correspond à une rotation dans M. Comme l'intervalle d'espace-temps doit être conservée en rotation, l'intervalle d'espace-temps doit être le même dans tous les cadres de référence. Dans la proposition 1, nous avons montré qu'il est nul dans un cadre de référence, par conséquent, il doit être à zéro dans tous les autres cadres de référence. Nous obtenons que

ce qui implique

Les chemins de rayons lumineux ont un intervalle d'espace-temps zéro, et donc tous les observateurs obtiendront la même valeur pour la vitesse de la lumière. Par conséquent, lorsque l'hypothèse que l'univers a quatre dimensions qui sont liés par la formule de Minkowski, la vitesse de la lumière apparaît comme une constante, et ne doit pas être pris (postulé) être constante comme dans l'approche originale de Einstein pour la relativité restreinte.

Horloge retards et de tige: contractions plus sur les transformations de Lorentz

Une autre conséquence de l'invariance de l'intervalle de l'espace-temps est que les horloges apparaîtront aller plus lentement sur des objets qui se déplacent par rapport à l'observateur. Ceci est très similaire à la façon dont la projection 2D d'une ligne mis en rotation dans la troisième dimension apparaît à se raccourcir. Longueur ne est pas conservée tout simplement parce que nous ignorons l'une des dimensions. Revenons à l'exemple de John et Bill.

John observe la longueur de l'intervalle de l'espace-temps de Bill comme:

alors que le projet de loi ne pense pas qu'il a voyagé dans l'espace, écrit:

L'intervalle de l'espace-temps, S ^2, est invariant. Il a la même valeur pour tous les observateurs, peu importe qui le mesure ou comment ils se déplacent en ligne droite. Cela signifie que l'intervalle de l'espace-temps de Bill égale l'observation de Jean de intervalle de l'espace-temps de Bill sorte:

et

d'où

.

Donc, si John voit une horloge qui est au repos dans le dossier de trame une secondes de Bill, John se trouve que ses propres mesures d'horloge entre ces mêmes tiques un intervalle t, appelé coordonner les temps, ce qui est supérieur à une seconde. Il est dit que les horloges en mouvement ralentissent, par rapport à ceux sur les observateurs au repos. Ceci est connu comme "relativiste dilatation du temps d'une horloge en mouvement ". Le temps qui est mesurée dans le cadre reste de l'horloge (dans le cadre de projet de loi) est appelé bon moment de l'horloge.

Dans la relativité restreinte, par conséquent, des changements dans référentiel affectent le temps aussi. Le temps ne est plus absolue. Il n'y a pas d'horloge universellement correcte; temps imparti à des taux différents pour les différents observateurs.

De même, il peut être démontré que John sera également observer piges au repos sur la planète le projet de loi à être plus courte dans le sens du mouvement que ses propres barres de mesure. Il se agit d'une prédiction dite "relativiste la contraction des longueurs d'une tige mobile ". Si la longueur d'une tige au repos sur la planète projet de loi est X, alors nous appelons cette quantité du bonne longueur de la tige. La longueur x de la même tige, mesurée sur la planète John, est appelée longueur de coordonner et donnée par

.

Comment les coordonnées de Bill semblent John à l'instant où ils se croisent

Ces deux équations peuvent être combinés pour obtenir la forme générale de la transformation de Lorentz dans une dimension spatiale:

ou de manière équivalente:

où le Facteur de Lorentz est donnée par

Les formules ci-dessus pour les retards d'horloge et contractions de longueur sont des cas particuliers de la transformation générale.

Alternativement, ces équations pour la dilatation du temps et de la contraction des longueurs (ici obtenues à partir de l'invariance de l'intervalle de l'espace-temps), peuvent être obtenues directement à partir de la transformation de Lorentz en mettant X = 0 pour la dilatation du temps, ce qui signifie que l'horloge est au repos dans le cadre de projet de loi, ou en réglant t = 0 pour la contraction des longueurs, ce qui signifie que John doit mesurer les distances aux points de la tige mobile finaux en même temps.

Une conséquence des transformations de Lorentz est l'modifiée formule vitesse-plus:

Simultanéité et l'horloge désynchronisation

La dernière conséquence de l'espace-temps de Minkowski est que les horloges seront semblent être en opposition de phase avec l'autre le long de la longueur d'un objet en mouvement. Cela signifie que si un observateur met en place une ligne d'horloges qui sont tous synchronisés afin qu'ils lisent tous en même temps, puis un autre observateur qui se déplace le long de la ligne à grande vitesse verra les horloges tous les différents moments de lecture. Cela signifie que les observateurs qui se déplacent par rapport à l'autre voir différents événements comme simultanée. Cet effet est connu comme "la phase relativiste» ou la «relativité de la simultanéité". La phase relativiste est souvent négligé par les étudiants de la relativité restreinte, mais si elle est comprise, alors phénomènes tels que la double paradoxe sont plus faciles à comprendre.

Le "plan de simultanéité" ou "surface de la simultanéité" contient tous les événements qui se produisent au même moment pour un observateur donné. Les événements qui sont simultanés pour un observateur ne sont pas simultanées pour un autre observateur en mouvement relatif.

Les observateurs ont un ensemble d'événements simultanés autour d'eux qu'ils considèrent comme composer l'instant présent. La relativité des résultats de simultanéité dans observateurs qui se déplacent par rapport à l'autre ayant différents ensembles d'événements dans leur instant présent.

L'effet net de l'univers à quatre dimensions est que les observateurs qui sont en mouvement par rapport à vous semblez avoir les coordonnées de temps qui se penchent plus dans la direction du mouvement, et d'envisager les choses soient simultanée qui ne sont pas simultanée pour vous. Longueurs spatiales dans le sens de Voyage sont raccourcis, parce qu'ils basculent vers le haut et vers le bas, par rapport à l'axe du temps dans le sens de Voyage, qui se apparente à un biais ou de cisaillement de l'espace en trois dimensions.

Un grand soin est nécessaire lors de l'interprétation des diagrammes d'espace-temps. Diagrammes données présentes dans deux dimensions, et ne peut pas montrer fidèlement comment, par exemple, un intervalle de l'espace-temps de la longueur de zéro apparaît.

La relativité générale: un coup d'oeil vers l'avant

Contrairement aux lois de Newton sur le mouvement, la relativité ne est pas basée sur des postulats dynamiques. Il ne assume rien sur le mouvement ou les forces. Au contraire, il traite de la nature fondamentale de l'espace-temps. Il se inquiète de décrire la géométrie de la toile de fond sur laquelle tous les phénomènes dynamiques se déroulent. En un sens donc, ce est un méta-théorie, une théorie qui définit une structure que toutes les autres théories doivent suivre. En vérité, la relativité restreinte est qu'un cas particulier. Il suppose que l'espace-temps est plat. Ce est, il suppose que la structure de l'espace de Minkowski et le tenseur métrique de Minkowski est constante tout au long. Dans la relativité générale , Einstein a montré que ce ne est pas vrai. La structure de l'espace-temps est modifiée par la présence de la matière. Plus précisément, la formule de la distance indiquée ci-dessus ne est généralement plus valables sauf dans l'espace libre de la masse. Cependant, tout comme une surface courbe peut être considéré comme plat dans la limite infinitésimale de calcul, un espace courbe peut être considéré comme plat à une petite échelle. Cela signifie que la métrique de Minkowski écrit sous la forme différentielle est généralement valable.

On dit que la métrique de Minkowski est valable localement, mais il ne parvient pas à donner une mesure de la distance sur de longues distances. Il ne est pas valable à l'échelle mondiale. En fait, dans la relativité générale se métrique mondiale devient dépendant de la distribution de masse et varie à travers l'espace. Le problème central de la relativité générale est de résoudre la célèbre Équation d'Einstein pour une distribution de masse donnée et trouver la formule de la distance qui se applique dans ce cas particulier. La formulation de l'espace-temps de Minkowski était l'intensification conceptuelle pierre pour la relativité générale. Son fondamentalement nouvelle perspective a permis non seulement le développement de la relativité générale, mais aussi dans une certaine mesure les théories quantiques des champs .

L'équivalence masse-énergie: la lumière du soleil et de bombes atomiques

Einstein a montré que la masse est simplement une autre forme d'énergie. L'équivalent énergétique de repos masse m est mc ^2. Cette équivalence implique que la masse doit être interconvertibles avec d'autres formes d'énergie. Ce est le principe de base derrière les bombes atomiques et la production d'énergie dans les réacteurs nucléaires et les étoiles (comme le Soleil).

Applications

Il ya une perception commune que la physique relativiste ne est pas nécessaire pour des raisons pratiques ou dans la vie quotidienne. Ce n'est pas vrai. Sans effets relativistes, l'or aurait l'air argentée, plutôt que jaune. Beaucoup de technologies dépendent de façon critique sur la physique relativiste:

• Tubes cathodiques,
• Les accélérateurs de particules,
• Global Positioning System (GPS) - bien que cela nécessite vraiment la théorie complète de la relativité générale

Les postulats de la relativité restreinte

Einstein a développé la relativité restreinte sur la base de deux postulats:

• Première postulat - spécial principe de relativité - Les lois de la physique sont les mêmes dans tous les référentiels inertiels. En d'autres termes, il n'y a pas de référentiels inertiels privilégiés de référence.
• Deuxième postulat - invariance de c - La vitesse de la lumière dans un vide est indépendante du mouvement de la lumière la source.

La relativité spéciale peut être dérivé de ces postulats, comme cela a été fait par Einstein en 1905. Les postulats d'Einstein sont toujours applicables dans la théorie moderne, mais l'origine des postulats est plus explicite. Il a été montré ci-dessus comment l'existence d'une vitesse constante universelle (la vitesse de la lumière) est une conséquence de la modélisation de l'univers comme un espace à quatre dimensions particulier ayant certaines propriétés spécifiques. Le principe de la relativité est le résultat de la structure Minkowski étant conservé par les transformations de Lorentz, qui sont postulés pour les transformations physiques de cadres de référence inertiels.