
Énergie cinétique
À propos de ce écoles sélection Wikipedia
Ce contenu de Wikipedia a été sélectionné par SOS Enfants d'aptitude dans les écoles à travers le monde. Une bonne façon d'aider d'autres enfants est de parrainer un enfant

L'énergie cinétique d'un objet est le supplément d'énergie qu'elle possède en raison de son mouvement. Il est défini comme le travail nécessaire pour accélérer un corps d'une masse donnée de repos à sa vitesse actuelle. Ayant acquis cette énergie au cours de son accélération , le corps maintient cette énergie cinétique à moins que ses changements de vitesse. Travail négatif de la même ampleur serait nécessaire pour retourner le corps à un état de repos à partir de cette vitesse.
Étymologie
| Chercher cinétique dans Wiktionary, le dictionnaire libre. |
L'adjectif «cinétique» au substantif énergie a ses racines dans le grec mot pour «motion» ( Kinesis). Les termes de l'énergie cinétique et de travail et de leurs significations scientifiques actuelles datent du milieu du 19ème siècle. Les premiers accords de ces idées peuvent être attribués à Gaspard-Gustave Coriolis qui en 1829 a publié le document intitulé Du Calcul de l'Effet des Machines décrivant les mathématiques de l'énergie cinétique.
William Thomson , plus tard Lord Kelvin, est donné le crédit pour inventer le terme énergie cinétique c. 1849.
Introduction
Il existe différentes formes d'énergie: énergie chimique, la chaleur , rayonnement électromagnétique , l'énergie potentielle (gravitationnelle, électrique, élastique, etc.), énergie nucléaire, énergie au repos. Ceux-ci peuvent être classés en deux catégories principales: énergie potentielle et l'énergie cinétique.
L'énergie cinétique peut être mieux compris par des exemples qui démontrent comment il est transformé à partir d'autres formes d'énergie et aux autres formes. Par exemple, un cycliste utilisera énergie chimique qui a été apporté par l'alimentation pour accélérer un vélo pour une vitesse choisie. Cette vitesse peut être maintenue sans la poursuite des travaux, à l'exception de surmonter résistance de l'air et la friction. L'énergie a été transformée en l'énergie du mouvement, connu comme l'énergie cinétique, mais le processus ne est pas totalement efficace et la chaleur est également produite dans le cycliste.
L'énergie cinétique dans le déplacement à vélo et de la cycliste peut être convertie en d'autres formes. Par exemple, le cycliste pourrait rencontrer une colline juste assez haut à l'autre, de sorte que le vélo vient à un arrêt complet au sommet. L'énergie cinétique est maintenant largement été convertie en énergie potentielle gravitationnelle qui peut être libéré par roue libre vers le bas de l'autre côté de la colline. (Depuis la bicyclette a perdu une partie de son énergie à la friction, il ne retrouvera jamais la totalité de sa vitesse sans pédaler. Notez que l'énergie ne est pas perdue, car il n'a été convertie en une autre forme par le frottement.) Sinon, le cycliste peut connecter un dynamo à l'une des roues et également générer de l'énergie électrique à la descente. Le vélo se rendrait plus lentement en bas de la colline parce que certains de l'énergie a été détourné dans la prise électrique. Une autre possibilité serait pour le cycliste d'appliquer les freins, dans ce cas, l'énergie cinétique serait dissipée par frottement que l'énergie thermique.
Comme toute grandeur physique qui est fonction de la vitesse, l'énergie cinétique d'un objet ne dépend pas seulement de la nature interne de cet objet. Elle dépend aussi de la relation entre l'objet et l'observateur (en physique un observateur est formellement défini par une classe particulière de système de coordonnées appelé référentiel inertiel). Grandeurs physiques de ce genre sont, dit-on pas invariant. L'énergie cinétique est co-localisés avec l'objet et contribue à son champ gravitationnel.
Calculs
Il existe plusieurs équations différentes qui peuvent être utilisées pour calculer l'énergie cinétique d'un objet. Dans de nombreux cas, ils donnent presque la même réponse à bien dans la précision mesurable. Si elles sont différentes, le choix de l'utiliser est déterminée par la vitesse du corps ou sa taille. Ainsi, si l'objet se déplace à une vitesse bien inférieure à la vitesse de la lumière, les mécaniciens (classiques) newtoniens seront suffisamment précis; mais si la vitesse est comparable à la vitesse de la lumière, la relativité commence à faire des différences significatives au résultat et doit être utilisé. Si la taille de l'objet est sub-atomique, la mécanique quantique équation est la plus appropriée.
L'énergie cinétique newtonienne
L'énergie cinétique des corps rigides
Dans la mécanique classique , l'énergie cinétique d'un "objet point" (un corps si petit que sa taille peut être ignoré), ou d'un non rotatif corps rigide, est donnée par l'équation 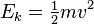 où m est la masse et v est la vitesse du corps.
où m est la masse et v est la vitesse du corps.
Par exemple - on peut calculer l'énergie cinétique d'un déplacement de masse 80 kg à 18 mètres par seconde (40 mph) en tant que 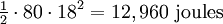 .
.
Notez que l'énergie cinétique augmente avec le carré de la vitesse. Cela signifie, par exemple, que si vous voyagez deux fois plus vite, vous aurez quatre fois plus d'énergie cinétique. À la suite de cela, une voiture roulant deux fois plus vite nécessite quatre fois plus de distance pour se arrêter (en supposant une force de freinage constante. Voir travail mécanique ).
Ainsi, l'énergie cinétique peut être calculée en utilisant la formule:
où:
- E k est l'énergie cinétique en joules
- m est la masse en kg, et
- v est la vitesse, en mètres par seconde.
Pour l'énergie cinétique de translation d'un corps dont la constante de masse m, dont le centre de masse se déplace en ligne droite à une vitesse v, comme on le voit ci-dessus est égal à
où:
- m est la masse du corps
- v est la vitesse du centre de masse du corps.
Ainsi l'énergie cinétique est une mesure relative et aucun objet ne peut être considéré comme ayant une énergie cinétique unique. Un moteur-fusée peut être considérée à transférer son énergie à la fusée ou dans le flux de gaz d'échappement en fonction de la trame de référence choisi. Mais l'énergie totale du système, ce est à dire l'énergie cinétique, l'énergie chimique du carburant, de l'énergie thermique, etc, sera conservée quel que soit le choix de la trame de sondage.
L'énergie cinétique d'un objet est en relation avec son élan par l'équation:
Calcul et définition
Le travail effectué accélérer une particule pendant l'intervalle de temps infinitésimal dt est donné par le produit scalaire de la force et le déplacement:
L'application de la règle du produit, nous voyons que:
Par conséquent (en supposant une masse constante), ce qui suit peut être vu:
Puisque ce est une différentielle totale (ce est, il ne dépend que de l'état final, pas comment la particule est arrivé là), nous pouvons intégrer et appeler le résultat de l'énergie cinétique:
Cette équation indique que l'énergie cinétique (E k) est égale à l' intégrale de la point produit de la vitesse (v) d'un corps et la changement infinitésimal de l'organisme l'élan (p). Il est supposé que le corps commence sans énergie cinétique quand il est au repos (immobile).
L'énergie cinétique des systèmes
Pour un seul point, ou un corps rigide qui ne est pas en rotation, l'énergie cinétique va à zéro lorsque le corps se arrête.
Cependant, pour les systèmes contenant plusieurs organes mobiles indépendamment, ce qui peut exercent des forces entre eux, et peut (ou non) être en rotation; ce ne est plus vrai.
Cette énergie est appelée «l'énergie».
L'énergie cinétique du système à tout instant dans le temps est simplement la somme des énergies cinétiques et par les masses, y compris l'énergie cinétique due aux rotations.
Un exemple serait le système solaire. Dans le centre de masse du système solaire, le Soleil est (presque) stationnaire, mais les planètes et les astéroïdes sont en mouvement à ce sujet. Ainsi, même dans un fixe centre du cadre de masse, il ya encore de l'énergie cinétique présente.
Cependant, recalculer l'énergie à partir de différents cadres serait fastidieux, mais il ya un truc. L'énergie cinétique du système à partir d'un référentiel inertiel différente peut être calculée simplement à partir de la somme de l'énergie cinétique dans le centre du cadre de masse et en ajoutant de l'énergie que la masse totale du corps dans le centre de masse aurait se il était se déplaçant à la vitesse relative entre les deux cadres.
Ce peut être simplement indiqué: soit V la vitesse relative de la trame k du centre de masse i:
Cependant, laissez-  l'énergie cinétique dans le centre de masse,
l'énergie cinétique dans le centre de masse,  serait tout simplement l'impulsion totale qui est par définition zéro dans le centre de masse, et laissez la masse totale:
serait tout simplement l'impulsion totale qui est par définition zéro dans le centre de masse, et laissez la masse totale:  . En substituant, on obtient:
. En substituant, on obtient:
L'énergie cinétique d'un système dépend donc de la repère inertiel et il est le plus bas par rapport au centre de masse repère de référence, ce est à dire, dans un cadre de référence dans lequel le centre de masse est à l'arrêt. Dans une autre trame de référence il se agit d'une énergie cinétique supplémentaire correspondant à la masse totale en mouvement à la vitesse du centre de masse.
Corps rotatifs
Si un corps rigide est en rotation sur une ligne passant par le centre de la masse alors qu'elle a énergie cinétique de rotation (  ) Qui est simplement la somme des énergies cinétiques de ses pièces mobiles, et il est donc égale à:
) Qui est simplement la somme des énergies cinétiques de ses pièces mobiles, et il est donc égale à:
où:
- ω est le corps de la vitesse angulaire .
- r est la distance de ne importe quelle masse dm de cette ligne
- I est le corps de moment d'inertie
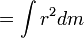
(Dans cette équation, le moment d'inertie doit être pris à un axe traversant le centre de masse et la rotation mesurée par ω doit être autour de cet axe; plusieurs équations générales existent pour les systèmes où l'objet est soumis à vaciller en raison de sa forme excentrique) .
La rotation dans les systèmes
Il est parfois commode de diviser l'énergie cinétique totale d'un corps en la somme du centre de masse du corps de l'énergie cinétique de translation et de l'énergie de rotation autour du centre de masse énergie de rotation:
où:
- E k est l'énergie cinétique totale
- T E est l'énergie cinétique de translation
- E r est l'énergie de rotation ou l'énergie cinétique angulaire dans le cadre de repos
Ainsi, l'énergie cinétique d'une balle de tennis en vol est l'énergie cinétique due à sa rotation, ainsi que l'énergie cinétique due à sa traduction.
L'énergie cinétique relativiste de corps rigides
Dans la relativité restreinte , nous devons changer l'expression de la quantité de mouvement. Intégration par parties, on obtient:
Se souvenant que  , On a:
, On a:
Et ainsi:
La constante d'intégration se trouve en observant que  quand
quand  , Ainsi nous obtenons la formule habituelle:
, Ainsi nous obtenons la formule habituelle:
Si la vitesse d'un corps est une fraction significative de la vitesse de la lumière , il est nécessaire d'utiliser la mécanique relativiste (la théorie de la relativité comme exposé par Albert Einstein ) pour calculer son énergie cinétique.
Pour un objet relativiste l'élan p est égal à:
 ,
,
où m est le masse au repos, v est la vitesse de l'objet, et c est la vitesse de la lumière dans le vide.
Ainsi, le travail dépensé accélérer un objet du repos à une vitesse relativiste est:
 .
.
L'équation montre que l'énergie d'un objet se approche de l'infini comme la vitesse v se approche de la vitesse de la lumière c, il est donc impossible d'accélérer un objet à travers cette frontière.
Le sous-produit mathématique de ce calcul est le formule l'équivalence masse-énergie corps au repos doit avoir un contenu d'énergie égale à:
A une vitesse faible (v <
 ,
,
Ainsi, l'énergie totale E peut être partitionné en l'énergie de la masse au repos, plus l'énergie cinétique newtonien classique à basse vitesse.
Lorsque les objets se déplacent à une vitesse beaucoup plus lente que la lumière (par exemple dans les phénomènes de tous les jours sur la Terre), les deux premiers termes de la série prédominent. Le prochain terme dans le rapprochement est faible pour les faibles vitesses, et peut être trouvé en étendant l'expansion dans une série de Taylor par un autre mandat:
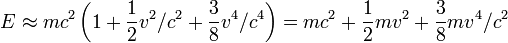 .
.
Par exemple, pour une vitesse de 10 km / s, la correction de l'énergie cinétique est newtonien 0,07 J / kg (sur une énergie cinétique de 50 newtonien MJ / kg) et pour une vitesse de 100 km / s, il est de 710 J / kg (sur une énergie cinétique newtonienne de 5 GJ / kg), etc.
Pour des vitesses supérieures, la formule de l'énergie cinétique relativiste est dérivé par la soustraction de l'énergie masse au repos de l'énergie totale:
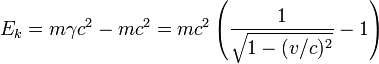 .
.
La relation entre l'énergie cinétique et la dynamique est plus compliqué dans ce cas, et est donné par l'équation:
 .
.
Cela peut aussi être développée en série de Taylor , le premier terme de ce qui est la simple expression de la mécanique newtonienne.
Ce que cela suggère est que les formules pour l'énergie et le dynamisme ne sont pas spécial et axiomatique, mais plutôt des concepts qui émergent de l'équation de la masse d'énergie et les principes de la relativité.
Quantum énergie cinétique mécanique des corps rigides
Dans le domaine de la mécanique quantique, la valeur moyenne de l'énergie cinétique des électrons,  , Par un système d'électrons décrit par la fonction d'onde
, Par un système d'électrons décrit par la fonction d'onde  est une somme de 1 électron valeurs opérateur d'attentes:
est une somme de 1 électron valeurs opérateur d'attentes:
où  est la masse de l'électron et
est la masse de l'électron et 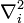 est le Opérateur laplacien agissant sur les coordonnées du i ème électrons et la sommation se étend sur tous les électrons. Notez que ce est la version quantifiée de l'expression non relativiste de l'énergie cinétique en termes de dynamique:
est le Opérateur laplacien agissant sur les coordonnées du i ème électrons et la sommation se étend sur tous les électrons. Notez que ce est la version quantifiée de l'expression non relativiste de l'énergie cinétique en termes de dynamique:
Le densité formalisme de la fonctionnelle de la mécanique quantique nécessite la connaissance de la densité électronique uniquement, ce est à dire, il ne exige pas formellement connaissance de la fonction d'onde. Compte tenu de la densité d'électrons 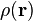 , La N-électrons l'énergie cinétique exacte fonctionnelle est inconnue; toutefois, pour le cas spécifique d'un système 1-électrons, l'énergie cinétique peut se écrire
, La N-électrons l'énergie cinétique exacte fonctionnelle est inconnue; toutefois, pour le cas spécifique d'un système 1-électrons, l'énergie cinétique peut se écrire
où ![T [\ rho]](../../images/173/17351.png) il est connu que l'énergie cinétique de Weizsâcker fonctionnel.
il est connu que l'énergie cinétique de Weizsâcker fonctionnel.
Quelques exemples
l'utilisation de l'engin spatial de l'énergie chimique de décoller et d'acquérir l'énergie cinétique considérable pour atteindre vitesse orbitale. Cette énergie cinétique acquise au cours de lancement restera constante en orbite parce qu'il n'y a pratiquement pas de frottement. Cependant il apparaît à la rentrée lorsque l'énergie cinétique est convertie en chaleur.
L'énergie cinétique peut être passée d'un objet à un autre. Dans le jeu de billard, le joueur donne de l'énergie cinétique à la boule en le frappant avec la queue de billard. Si la bille blanche entre en collision avec une autre balle, il va ralentir de façon spectaculaire et le ballon est entré en collision avec la volonté d'accélérer à une vitesse que l'énergie cinétique est passé sur elle. Collisions en billard sont effectivement collisions élastiques, où l'énergie cinétique est préservée.
Volants sont développés comme une méthode de stockage de l'énergie (voir l'article volant de stockage d'énergie). Cela montre que l'énergie cinétique de rotation peut également être. Notez la formule dans les articles sur les volants pour le calcul de l'énergie cinétique de rotation est différente, mais analogue.
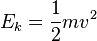


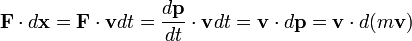
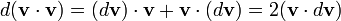
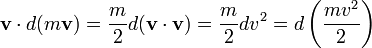



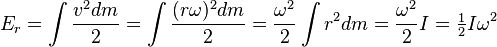





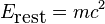

![T [\ rho] = \ frac {1} {8} \ int \ frac {\ nabla \ rho (\ mathbf {r}) \ cdot \ nabla \ rho (\ mathbf {r})} {\ rho (\ mathbf {r})} ^ D 3r](../../images/173/17350.png)
