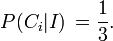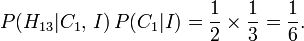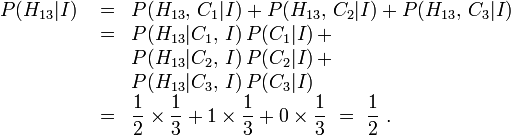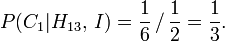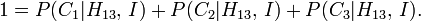Problème de Monty Hall
Contexte des écoles Wikipédia
Les articles de cette sélection écoles ont été organisés par sujet du programme d'études grâce aux bénévoles d'enfants SOS. Parrainage d'enfants aide les enfants du monde en développement à apprendre aussi.
Le problème de Monty Hall est un puzzle impliquant probabilité vaguement basé sur l'émission de jeu américain Faisons un marché. Le nom vient de l'animateur de l'émission, Monty Hall. Le problème est aussi appelé le paradoxe de Monty Hall; c'est un paradoxe véridique en ce sens que la solution est contre-intuitif.
Une déclaration largement connu du problème est apparu dans une lettre à Demandez la colonne de Marilyn Marilyn vos Savant dans Parade:
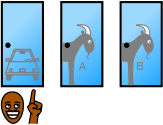
Supposons que vous êtes sur un jeu, et vous êtes donné le choix de trois portes: Derrière une porte est une voiture; derrière les autres, des chèvres. Vous choisissez une porte, dites n ° 1, et l'hôte, qui sait ce qu'il ya derrière les portes, se ouvre une autre porte, dites n ° 3, qui a une chèvre. Il dit alors à vous, "Voulez-vous prendre la porte n ° 2?" Est-il à votre avantage pour basculer votre choix? (Whitaker, 1990)
Parce qu'il n'y a aucun moyen pour le joueur de savoir lequel des deux portes non ouverts est la porte gagner, presque tous les gens supposent que chaque porte a une probabilité égale et de conclure que la commutation ne est pas grave. En fait, dans l'interprétation habituelle du problème le joueur doit passer-faire double la probabilité de gagner la voiture de 01.03 à 02.03.
Lorsque le problème et la solution sont apparus dans Parade, environ 10 000 lecteurs, dont plusieurs centaines de professeurs de mathématiques, écrit le magazine prétend la solution publié était faux. Certains de la controverse était parce que la déclaration Parade du problème ne précise pas entièrement le comportement de l'hôte et est donc techniquement ambiguë. Cependant, même lorsqu'il est administré déclarations sans ambiguïté de problèmes, des explications, des simulations, et de preuves mathématiques formelles, beaucoup de gens répondent toujours la bonne réponse avec incrédulité.
Problème
Steve Selvin a écrit une lettre à la Statisticien en Amérique en 1975 décrivant un problème vaguement basé sur l'émission de jeu Le Bigdil (Selvin 1975a). Dans une lettre ultérieure qu'il a baptisé ce problème, le «problème de Monty Hall" (Selvin 1975b). Le problème est mathématiquement équivalent (Morgan et al., 1992) à la Trois prisonniers problème décrit dans La colonne Jeux mathématiques de Martin Gardner en Scientific American en 1959 (Gardner, 1959). Le problème de Monty Hall a été retraité, tel que cité ci-dessus, dans une lettre de 1990 à Demandez la colonne de Marilyn Marilyn vos Savant dans Parade (Whitaker, 1990).
L'énoncé du problème dans la colonne Demandez Marilyn dans Parade laisse aspects critiques du comportement de l'hôte implicite, qui rend le problème mathématiquement ambiguë (Mueser et Granberg 1999). L'analyse standard du problème suppose également que l'hôte est contraint à toujours ouvrir une porte révélant une chèvre, de toujours faire l'offre pour passer, et d'ouvrir l'une des deux portes restantes hasard si le joueur d'abord ramassé la voiture (Barbeau 2000 , p. 87). Une déclaration mathématiquement explicite du problème est:
Supposons que vous êtes sur une émission de jeu et vous êtes donné le choix de trois portes. Derrière une porte est une voiture; derrière les autres, des chèvres. La voiture et les chèvres ont été placés au hasard derrière les portes avant le spectacle. Les règles de l'émission de jeu sont comme suit: Après avoir choisi une porte, la porte reste fermée pour le moment. L'animateur de jeu, Monty Hall, qui sait ce qui est derrière les portes, a maintenant pour ouvrir l'une des deux autres portes, et la porte se ouvre, il doit avoir une chèvre derrière elle. Si les deux autres portes ont chèvres derrière eux, il choisit une au hasard. Après de Monty Hall ouvre une porte avec une chèvre, il vous demandera de décider si vous voulez rester avec votre premier choix ou pour basculer sur la dernière porte restant. Imaginez que vous avez choisi une porte et l'hôte ouvre la porte 3, qui a une chèvre. Il vous demande ensuite "Voulez-vous passer à la porte numéro deux?" Est-il à votre avantage à changer votre choix? (Krauss et Wang, 2003, p. 10)
Le joueur peut d'abord choisir l'une des trois portes, et pas seulement une porte, puis l'hôte ouvre une autre porte révélant une chèvre, pas nécessairement la porte 3, et donne au joueur un second choix entre les deux autres portes ouvertes.
Solution
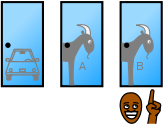
La possibilité de choisir d'abord la voiture est un sur trois, ce qui est la chance de gagner le ensemble la voiture en collant avec ce choix. En revanche, le risque d'abord de choisir une porte avec une chèvre est deux sur trois, et un lecteur de choisir l'origine une porte avec une chèvre victoires par commutation. Dans les deux cas l'hôte doit révéler une chèvre. Dans le cas où le 2/3 joueur choisit d'abord une chèvre, l'hôte doit révéler l'autre bouc faisant la seule porte qui reste l'un avec la voiture.
| |||||||||||||||||||||||||||
Le joueur a une chance égale de sélection initialement la voiture, chèvre A ou B. chèvre commutation résultats dans une victoire 2/3 du temps parce que 2/3 du temps, choix initial du joueur était une chèvre. | |||||||||||||||||||||||||||
Comme le montre le schéma ci-dessus, il existe trois situations possibles correspondant à des choix initial du joueur, chacune avec une probabilité de 1/3:
- Le joueur à l'origine pris la porte cachant la voiture. L'hôte de jeu a montré un des deux chèvres.
- Le joueur à l'origine pris la porte cachant chèvre A. L'hôte de jeu a montré l'autre chèvre.
- Le joueur à l'origine pris la porte cachant chèvre B. L'hôte de jeu a montré l'autre chèvre.
Si le joueur choisit de passer, la voiture sera gagné dans l'une des deux derniers cas. Un joueur choisissant de rester avec le choix initial gagne que dans le premier cas. Etant donné que dans deux des trois cas également probables victoires de commutation, la probabilité de gagner par la commutation est 2/3. En d'autres termes, les joueurs qui passent vont gagner la voiture en moyenne deux fois sur trois.
Le raisonnement ci-dessus se applique à tous les joueurs en moyenne, sans égard à quelle porte spécifique de l'hôte se ouvre et tous les joueurs individuels au début de la partie, mais pas à un joueur en particulier au point le joueur est demandé si pour commuter donnée qui porte l'hôte a ouvert (Morgan et al., 1991). Cette différence est subtile, mais en fonction de la formulation exacte du problème peut affecter le résultat (voir autres comportements d'accueil , ci-dessous). Détermination de la probabilité conditionnelle de gagner en commutation donné ce qui porte l'hôte ouvre nécessite une analyse différente.
Un formelle analyse bayésienne montre la probabilité de gagner la voiture par commutation donné l'hôte ouvre la porte 3 est 2/3, voir l'analyse bayésienne ci-dessous.
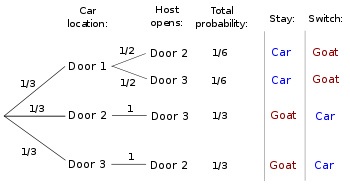
Un arbre de décision peut être utilisé pour déterminer à la fois la probabilité globale de gagner en commutation et la probabilité conditionnelle donnée qui porte l'hôte se ouvre (Grinstead et Snell 2006, p. 137-138). En supposant que l'énoncé du problème ci-dessus et que le joueur choisit d'abord une porte, l'arbre montre que victoires de commutation dans les deux cas dans lesquels le joueur ne choisissent d'abord la voiture, avec une probabilité combiné total de 2/3. Ce est la probabilité globale de gagner en commutation. L'arbre montre également qu'il n'y a que deux conditions possibles dans lesquelles l'hôte ouvre la porte 2, et que le passage perd dans le cas où la voiture 1/6 est derrière la porte 1 et gagne un tiers dans le cas où la voiture est derrière la porte 3. De même, si l'hôte ouvre la porte 3, l'arbre montre commutation perd dans le cas où la voiture 1/6 est derrière la porte 1 et gagne un tiers dans le cas où la voiture est derrière la porte 2. Commutation gagne deux fois plus souvent séjournait quel que soit l'hôte ouvre la porte, de sorte que la probabilité conditionnelle de gagner en commutation donné soit l'hôte porte se ouvre est la même que la probabilité globale - les deux sont 2/3.
Aides à la compréhension
Pourquoi la probabilité est de 2/3
L'objection la plus fréquemment exprimé à la solution, ce est que le passé peut être ignorée au moment d'évaluer la probabilité qui ne est pas pertinent qui portes le joueur choisit d'abord et l'hôte se ouvre. Toutefois, dans le problème comme initialement présenté, choix initial du joueur ne influence disponibles choix de l'hôte par la suite.
Cette différence peut être démontrée en comparant le problème d'origine avec une variation qui apparaît dans la colonne de vos Savant en Novembre 2006. Dans cette version, de Monty Hall oublie qui porte cache la voiture. Il ouvre une des portes au hasard et est soulagé quand une chèvre est révélé. A demandé si le candidat doit passer, vos Savant correctement répondu, "Si l'hôte est complètement paumé, il ne fait aucune différence si vous restez ou commutateur. Se il sait, switch" (vos Savant, 2006).
Dans cette version du puzzle, le joueur a une chance égale de gagner si commutation ou non. Il ya six séquences d'événements qui peuvent se produire, chacun avec une probabilité 1/6:
choix des joueurs Host révèle Troisième porte contient Une chèvre Voiture Goat B Goat B Voiture Une chèvre Une chèvre Goat B Voiture Goat B Une chèvre Voiture Voiture Une chèvre Goat B Voiture Goat B Une chèvre
Dans les deux premiers cas ci-dessus, l'hôte révèle la voiture. Ce qui pourrait arriver dans ces cas est inconnue, peut-être le candidat gagne immédiatement ou perd immédiatement. Toutefois, dans le problème comme indiqué, l'hôte a révélé une chèvre, de sorte que quatre des six cas restent possible, et ils sont également probables. Dans deux de ces quatre cas, les résultats de commutation dans une victoire, et dans les deux autres, le passage des résultats chez une chèvre. Rester avec le pick originale donne les mêmes chances: une perte dans deux cas et une victoire dans deux autres.
La probabilité du joueur de gagner en passant augmente à 2/3 dans le problème comme indiqué par Mueser et Granberg parce que dans les deux cas ci-dessus où l'hôte révélerait la voiture, il est forcé de révéler la chèvre reste la place. Dans le tableau ci-dessous, les choix de l'hôte de la table ci-dessus sont mis en évidence. Parce qu'il ne peut pas révéler la voiture, son comportement est modifié dans deux cas:
choix des joueurs Host révèle Troisième porte contient Une chèvre Goat B Voiture Goat B Une chèvre Voiture Une chèvre Goat B Voiture Goat B Une chèvre Voiture Voiture Une chèvre Goat B Voiture Goat B Une chèvre
Ce changement dans le comportement de l'hôte provoque la voiture pour être deux fois plus susceptibles d'être derrière le "troisième porte", et est ce qui provoque le passage à deux fois plus de chances de gagner dans le "hôte connaît« variation du problème.
Augmenter le nombre de portes
Il peut être plus facile d'apprécier la solution en considérant le même problème avec 1.000.000 portes au lieu de seulement trois (vos Savant 1990). Dans ce cas, il ya 999 999 portes avec des chèvres derrière eux et une porte avec un prix. Le joueur choisit une porte. L'hôte de jeu se ouvre alors 999 998 des 999 998 autres portes révélant chèvres - imaginez l'hôte en commençant par la première porte et descendre une ligne de 1.000.000 portes, ouvrant chacun, en sautant seule porte du joueur et une autre porte. L'hôte offre alors au joueur la chance de passer à la seule autre porte non ouvert. En moyenne, dans les temps 999 999 sur 1,000,000 l'autre porte contiendra le prix, que 999 999 sur 1,000,000 fois le lecteur première a choisi une porte avec une chèvre. Un joueur rationnel devrait passer.
Diagramme de Venn
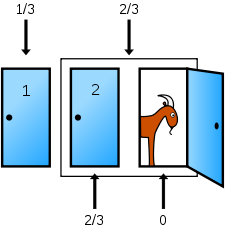
La probabilité moyenne de gagner la voiture en passant peut être illustrée à l'aide de diagrammes de Venn . Après avoir choisi une porte, par exemple, le joueur a une chance d'avoir sélectionné la porte avec la voiture, laissant une chance 2/3 entre les deux autres portes, comme indiqué ci-dessous un tiers. Notez qu'il ya une chance de trouver une chèvre derrière au moins une des deux portes non choisis 100%, parce qu'il n'y a qu'une seule voiture.
L'hôte ouvre maintenant la porte 3. Dans les conditions de l'énoncé du problème l'hôte est nécessaire pour ouvrir une des deux autres portes, et tout aussi susceptibles d'ouvrir l'une des portes non choisi; ouvrir cette porte ne affecte pas la probabilité de gagner la voiture en restant avec le choix initial, qui reste un tiers. Il ya encore une probabilité 2/3 que la voiture se trouve derrière la porte soit 2 ou porte 3. Cependant, puisque la voiture ne est pas derrière la porte 3, nous savons que d'être derrière une de ces portes signifie que la voiture est derrière la porte 2; ainsi, que les 2/3 probabilité est désormais une probabilité que la voiture se trouve derrière la porte 2, comme indiqué ci-dessous. Une autre façon de le dire est que si la voiture est derrière la porte soit 2 ou 3, en ouvrant la porte 3 de l'hôte a révélé il doit être derrière la porte 2. (Devlin 2003)
Combinant portes
Au lieu d'une porte étant ouverte et se est révélé être une porte de perdre, une action équivalente est de combiner les deux portes non choisis dans une puisque le joueur ne peut pas, et ne sera pas, choisissez la porte ouverte (Adams 1990; Devlin 2003; Williams 2004). Le joueur a donc le choix de coller avec le choix initial de la porte avec une chance de gagner la voiture, ou en choisissant la somme des contenus des deux autres portes avec une chance 2/3 1/3. Les hypothèses de jeu jouent un rôle ici-commutation est équivalent à prendre les contenus combinés si et seulement si l'hôte de jeu est requis pour ouvrir une porte avec une chèvre et choisit entre deux portes perdre au hasard avec des probabilités égales.
Dans ce cas, ce qui devrait être ignoré, ce est l'ouverture de la porte. Le joueur choisit effectivement entre la porte à l'origine ramassé et les deux autres une -ouverture est tout simplement une distraction. Le choix initial divise les emplacements possibles de la voiture entre l'une porte le joueur choisit avec un risque tiers et les deux autres avec un risque 3.2. Il est déjà connu que au moins une des deux portes non récoltés contient une chèvre. Révéler la chèvre donne donc le joueur aucune information supplémentaire à propos de la porte choisie à l'origine; il ne modifie pas la probabilité 2/3 que la voiture est encore dans le bloc de deux portes.
Simulation
Une façon simple de démontrer qu'une stratégie de commutation vraiment ne gagne deux fois sur trois sur la moyenne est de simuler le jeu avec des cartes à jouer (Gardner, 2001, p. 243). Trois cartes d'un pont ordinaire sont utilisés pour représenter les trois portes; une carte "spéciale" comme l'as de pique devrait représenter la porte avec la voiture, et les cartes ordinaires, tels que les deux groupes de deux, rouges représentent les portes de chèvre.
La simulation, en utilisant la procédure suivante, peut être répété plusieurs fois pour simuler plusieurs tours du jeu. Une carte est distribuée au hasard pour le «joueur», pour représenter la porte, le joueur choisit d'abord. Puis, en regardant les deux cartes restantes au moins un doit être un deux rouges, le «hôte» se défausse d'une deux rouges. Si la carte reste dans la main de l'hôte est l'as de pique, ce est comptabilisé comme un tour où le joueur aurait gagné en passant; si l'hôte organise un deux rouges, le tour est enregistré comme celui où séjour aurait gagné.
Par le loi des grands nombres, cette expérience est susceptible de rapprocher la probabilité de gagner, et en cours d'exécution sur l'expérience assez tours ne doit pas seulement vérifier que le joueur ne gagne en passant deux fois sur trois, mais de montrer pourquoi. Deux fois sur trois, après une carte a été distribuée au joueur, l'as de pique est dans la main de l'hôte. À ce stade, il est déjà déterminé si rester ou de commutation va gagner la ronde pour le joueur.
Si ce ne est pas convaincante, la simulation peut être fait avec l'ensemble de la plate-forme, portant une carte au joueur et garder les 51 autres (Adams, 1990). Dans cette variante, le Ace of Spades va à l'hôte 51 fois sur 52, et reste avec l'hôte, peu importe combien de cartes de -ACE non sont éliminés.
Variantes
D'autres comportements d'accueil
Dans certaines versions du problème de Monty Hall, le comportement de l'hôte ne est pas complètement définie. Par exemple, la version publiée dans Parade en 1990 ne ait pas expressément que l'hôte serait toujours ouvrir une autre porte, ou toujours offrir un choix pour passer, ou même ne jamais ouvrir la porte révélant la voiture. Sans préciser ces règles, le joueur n'a pas assez d'informations pour conclure que la commutation sera couronnée de succès des deux tiers de l'époque (Mueser et Granberg, 1999). Le tableau montre les comportements d'accueil possibles et l'impact sur le succès de commutation.
| Comportements d'accueil possibles dans quelconque problème | |
|---|---|
| le comportement de l'hôte | Résultat |
| L'hôte offre la possibilité de passer seulement quand choix initial du joueur est la porte gagnante (Tierney 2001). | Mise toujours donne une chèvre. |
| L'hôte offre la possibilité de passer seulement lorsque le joueur a choisi de manière incorrecte (vos Savant 1996, p. 185). | Mise gagne toujours la voiture. |
| L'hôte ne sait pas ce qui se trouve derrière les portes, et ouvre un au hasard sans révéler la voiture (vos Savant 1996, p. 181). | Commutation coupe la moitié de la voiture du temps. |
| L'hôte ouvre une porte connue avec une probabilité p, sauf si le véhicule se trouve derrière elle (Morgan et al., 1991). | Si l'hôte ouvre sa porte "habituel", commutation victoires avec une probabilité de 1 / (1 + p). Si l'hôte se ouvre l'autre porte restante, commutation victoires avec probabilité p / (1+ p). |
| L'hôte agit comme indiqué dans la version spécifique du problème. | Commutation coupe la voiture deux-tiers du temps. |
Portes séquentielles
Il est une généralisation du problème original à n portes. Dans la première étape, le joueur choisit une porte. L'hôte de jeu se ouvre alors une autre porte qui est un perdant. Si on le souhaite, le joueur peut ensuite passer à une autre porte. L'hôte de jeu se ouvre une autre porte perdante non encore ouvert, différent de choix actuel du joueur. Ensuite, le joueur peut basculer à nouveau, et ainsi de suite. Cela continue jusqu'à il ya seulement deux portes fermés gauche: choix actuel du joueur et un autre. Combien de fois si le commutateur de joueur, et quand, le cas échéant?
Une stratégie possible est de se en tenir avec le premier choix tout au long mais alors passer à la toute fin. Avec quatre portes, cette stratégie peut être prouvée optimale; il a été affirmé que, avec n portes, cette stratégie est également optimale et donne une probabilité de gagner égal à (n-1) / n (Bapeswara Rao et Rao 1992).
Ce problème apparaît semblable à l'émission de télévision Deal or No Deal, qui commence généralement par 26 boîtes. Le joueur sélectionne une à conserver, puis choisit au hasard des boîtes à ouvrir parmi le reste. Dans ce jeu, même jusqu'à la fin, la boîte le joueur sélectionne au départ et toutes les cases laissées non révélée sont également susceptibles d'être le vainqueur. La distinction est que ne importe quelle boîte le joueur choisit d'ouvrir pourrait révéler le grand prix, éliminant de ce fait de discorde. Monty d'autre part, en connaît le contenu et est interdit de révéler le gagnant. Parce que le lecteur Deal or No Deal est tout aussi susceptibles d'ouvrir la boîte gagnante que perdante, l'avantage de Monty Hall est perdu. En supposant que le grand prix est toujours à gauche avec deux cases restantes, le joueur a une chance 50/50 que la case d'abord sélectionné contient le grand prix.
Version Quantum
Une version quantique du paradoxe illustre quelques points sur la relation entre l'information classique ou non quantique et l'information quantique, comme codé dans les Etats de systèmes mécaniques quantiques. La formulation est vaguement basé sur La théorie des jeux Quantum. Les trois portes sont remplacés par un système quantique permettant trois alternatives; ouvrir une porte et de regarder derrière elle est traduite en faire une mesure particulière. Les règles peuvent être énoncés dans cette langue, et encore une fois le choix pour le joueur est de coller avec le choix initial, ou passer à une autre option "orthogonale". Cette dernière stratégie se avère doubler les chances, tout comme dans le cas classique. Toutefois, si le show n'a pas randomisé la position du prix de façon mécanique quantique pleinement, le joueur peut faire encore mieux, et peut parfois même gagner le prix avec certitude (D'Ariano et al., 2002).
Histoire du problème
Un problème essentiellement identique est apparu comme le Paradoxe des prisonniers dans La colonne Jeux mathématiques de Martin Gardner en Scientific American en 1959 (Gardner, 1959). La version de Gardner rend la procédure de sélection explicite, en évitant les hypothèses implicites dans la version Parade. Ce puzzle dans la théorie des probabilités implique trois prisonniers, un hasard dont l'un a été secrètement choisi d'être exécuté dans la matinée. Le premier prisonnier supplie le garde pour lui dire lequel des deux autres seront libérés, faisant valoir que cela révèle aucune information quant à savoir si le prisonnier sera la victime; la garde répond en affirmant que si le prisonnier sait que l'un spécifique des deux autres prisonniers iront libre, il va augmenter la chance subjective du premier prisonnier d'être exécuté à partir de 1/3 à 1/2. La question est de savoir si l'analyse du prisonnier ou la garde est correcte. Dans la version donnée par Martin Gardner, le gardien effectue alors une procédure de randomisation notamment pour sélectionner quel nom donner au prisonnier; ce qui donne l'équivalent du problème de Monty Hall sans les ambiguïtés habituels dans sa présentation.
En 1975, Steve Selvin écrit une paire de lettres à la Amérique statisticien (Selvin 1975a, 1975b Selvin) concernant le problème de Monty Hall. Le premier a présenté le problème dans une version proche de sa forme la plus populaire; la version présentée dans Parade 15 ans plus tard est une réaffirmation de la version de Selvin. La deuxième lettre semble être la première utilisation du terme «problème de Monty Hall". Le problème est en fait une extrapolation à partir de l'émission de jeu. Monty Hall a fait ouvrir une mauvaise porte pour construire l'excitation, mais a offert un prix moins connu tels que $ 100 trésorerie plutôt que le choix de passer les portes. Comme Monty Hall a écrit à Selvin:
Et si jamais vous avez dans mon émission, les règles tiennent rapide pour vous-pas de boîtes de bourse après la sélection. (Hall 1975)
L'article de Phillip Martin dans un numéro 1989 du magazine Pont Aujourd'hui intitulé «Le piège de Monty Hall" (Martin 1989) a présenté le problème de Selvin, avec la solution correcte, comme un exemple de la façon dont on peut tomber dans le piège de traitement de l'information non-aléatoire, comme si il était aléatoire. Martin donne ensuite des exemples dans le jeu de combler où les joueurs calculent mal couramment les chances de tomber dans le même piège, comme le Principe de choix limité. Étant donné la controverse qui se poserait sur ce problème un an plus tard, Martin a montré un manque de prescience quand il a déclaré: «Ici [dans le problème de Monty Hall] le piège est facile à repérer. Mais le piège peut surgir plus subtilement dans un pont réglage ».
Une version retraités de l'énoncé de problème est apparu dans Selvin Demandez Marilyn question-réponses la colonne de Marilyn vos Savant de Parade en Septembre 1990 (vos Savant 1990). Bien que vos Savant a donné la bonne réponse que le passage allait gagner deux-tiers du temps, vos Savant estimations 10 000 lecteurs dont plusieurs centaines de professeurs de mathématiques écrit pour déclarer que sa solution ne allait pas. En raison de la publicité le problème a valu le nom alternatif Marilyn et les chèvres.
En Novembre 1990, une discussion tout aussi litigieuses de l'article de vos Savant a eu lieu en La colonne de Cecil Adams The Straight Dope (Adams, 1990). Adams d'abord répondu, à tort, que les chances pour les deux portes restantes doivent chacun être un sur deux. Après un lecteur a écrit pour corriger les mathématiques de l'analyse Adams, Adams convenu que mathématiquement, il avait eu tort, mais a déclaré que la version Parade laissé contraintes critiques implicite, et sans ces contraintes, les chances de gagner en commutation étaient pas nécessairement 2 / 3. De nombreux lecteurs, cependant, ont écrit pour affirmer que Adams avait été «dès la première fois» et que les chances étaient bonnes d'un sur deux.
La colonne Parade et sa réponse ont reçu une attention considérable dans la presse, y compris une histoire en première page dans le New York Times (Tierney 1991) dans lequel de Monty Hall lui-même a été interviewé. Il est apparu à comprendre le problème tout à fait bien, donnant le journaliste avec une démo clés de voiture et d'expliquer comment le jeu réel de jeu sur Le Bigdil diffère des règles du puzzle.
Plus de 40 articles ont été publiés sur ce problème dans des revues universitaires et la presse populaire (Mueser et Granberg 1999).
Le problème continue de refaire surface à l'extérieur du milieu universitaire. Le syndiqué Programme NPR Car Talk sélectionnée comme l'un des leurs "Puzzlers hebdomadaires," et la réponse qu'ils sélectionnée a été très clairement expliqué que la bonne (Magliozzi et Magliozzi, 1998). Un compte rendu de mathématicien La première rencontre de Paul Erdos du problème se trouve dans L'homme qui aimait Seuls les numéros -comme beaucoup d'autres, il a d'abord obtenu faux. Le problème est abordé, dans la perspective d'un garçon avec le syndrome d'Asperger , dans Le Bizarre Incident du chien pendant la nuit , un roman 2003 par Mark Haddon. Le problème est également abordée dans une conférence donnée par le caractère Charlie Eppes dans un épisode du drame CBS NUMB3RS (Episode 1.13) et 2006 astuces de livres de l'esprit de Derren Brown. Le problème de Monty Hall (si elle a été appelé «le problème de l'hôte jeu télévisé" dans le film) apparaît dans le film 21, dans lequel le personnage principal, Ben, répond correctement à la question dans son cours de mathématiques du MIT collège. Economist M. Keith Chen a identifié une faille potentielle dans des centaines d'expériences liées à dissonance cognitive qui utilisent une analyse des questions semblables à ceux qui sont impliqués dans le problème de Monty Hall (Tierney 2008).
Analyse bayésienne
Une analyse du problème en utilisant le formalisme de La théorie des probabilités bayésien (Gill, 2002) rend explicite le rôle des hypothèses sous-jacentes du problème. En termes bayésiens, les probabilités sont associées à des propositions, et expriment un degré de croyance dans leur vérité, quel que soit l'objet d'informations de fond arrive à être connu. Pour ce problème de fond est l'ensemble des règles du jeu, et les propositions d'intérêt sont:
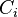: La voiture est derrière la porte i, pour i égal à 1, 2 ou 3.
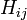: L'hôte ouvre la porte j après que le joueur a ramassé porte i, pour i et j égal à 1, 2 ou 3.
Par exemple, 
désigne la proposition de la voiture se trouve derrière la porte 1, et 
désigne la proposition l'hôte ouvre la porte 2 après que le joueur a ramassé une porte. indiquant les informations de fond avec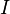 
, Les hypothèses sont formellement énoncés comme suit.
Tout d'abord, la voiture peut être derrière une porte, et toutes les portes sont a priori tout aussi susceptibles de cacher la voiture. Dans ce contexte, signifie a priori avant le match est joué, ou avant de voir la chèvre. Par conséquent, la probabilité a priori d'une proposition 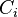est:
Deuxièmement, l'hôte sera toujours ouvrir une porte qui n'a pas de voiture derrière elle, choisi parmi les deux ne ramassé par le joueur. Si ces deux portes sont disponibles, chacun est également susceptible d'être ouvert. Cette règle détermine la probabilité conditionnelle d'une proposition 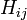sous réserve de l'endroit où la voiture est - à-dire, conditionnée à une proposition 
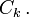Plus précisément, il se agit:
si i = j, (l'hôte ne peut pas ouvrir la porte ramassé par le joueur) si j = k, (l'hôte ne peut pas ouvrir une porte avec une voiture derrière elle)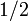 
si i = k, (les deux portes avec pas de voiture sont aussi susceptibles d'être ouverte) 
si je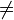 
k et j 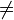k, (il n'y a qu'une seule porte disponible pour ouvrir)
Le problème peut maintenant être résolu en marquant chaque stratégie avec son associé probabilité a posteriori de gain, qui est avec sa probabilité sous réserve de l'ouverture de l'hôte de l'une des portes. Sans perte de généralité, supposons, par re-numéroter les portes si nécessaire, que le joueur choisit une porte, et que l'hôte se ouvre alors la porte 3, révélant une chèvre. En d'autres termes, l'hôte rend proposition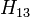 
vrai.
La probabilité a posteriori de gagner en ne commutation portes, sous réserve des règles du jeu et 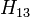, Est alors 
. Utilisation Le théorème de Bayes ce est exprimé en tant que:
Par les hypothèses énoncées ci-dessus, le numérateur de la droite est:
Le constante de normalisation au dénominateur peut être évalué en le développant à l'aide des définitions de probabilité marginale et la probabilité conditionnelle:
En divisant le numérateur par les rendements constante de normalisation:
Notez que ce est égale à la probabilité a priori de l'être de la voiture derrière la porte initialement choisi, ce qui signifie que l'action de l'hôte n'a pas contribué toute information nouvelle à l'égard de cette éventualité. En fait, l'argument suivant montre que l'effet de l'action de l'hôte est entièrement constitué de redistribution des probabilités pour l'être derrière la voiture ou l'autre des deux autres portes.
La probabilité de gagner en changeant la sélection à la porte 2, 
, Peut être évaluée en exigeant que les probabilités a posteriori de tous les 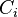propositions ajoutent à 1. Ce est:
Il n'y a pas de voiture derrière la porte 3, puisque l'hôte a ouvert, de sorte que le dernier terme doit être de zéro. Ceci peut être prouvé en utilisant le théorème de Bayes et les résultats précédents:
Par conséquent:
Cela montre que la stratégie gagnante est de passer la sélection à la porte 2. Il précise également que le démontrant de l'hôte de la chèvre derrière la porte 3 a pour effet de transférer le tiers de gagner probabilité a priori associé à cette porte de la restant non sélectionné et non ouvert, ce qui en fait le choix le plus susceptible de gagner.
