Archimède

Archimède de Syracuse (En grec: Ἀρχιμήδης)
Archimède réfléchie par Fetti (1620)
Né	c. 287 BC Syracuse, Sicile Magna Graecia
Mort	c. 212 BC (environ 75 ans) Syracuse
Résidence	Syracuse, Sicile
Les champs	Mathématiques Physique Ingénierie Astronomie Invention
Connu pour	Le principe d'Archimède La vis d'Archimède hydrostatique leviers infinitésimaux

Archimède de Syracuse ( grec : . Ἀρχιμήδης;. C 287 BC - 212 BC c) était un Mathématicien grec, physicien, ingénieur, inventeur, et astronome. Bien que peu de détails sur sa vie sont connus, il est considéré comme l'un des principaux scientifiques dans antiquité classique. Parmi ses avances dans la physique sont les fondements de hydrostatique, statique et une explication du principe de la levier. Il est crédité de la conception innovante machines, y compris engins de siège et la pompe à vis qui porte son nom. Les expériences modernes ont testé revendications qu'Archimède conçu machines capables de soulever des navires d'attaque hors de l'eau et la mise navires sur le feu en utilisant un réseau de miroirs.

Archimède est généralement considéré comme le plus grand mathématicien de l'Antiquité et un des plus grands de tous les temps. Il a utilisé le Procédé d'épuisement de calculer l' aire sous un arc de avec la parabole sommation d'une série infinie, et a donné une approximation remarquablement précis de pi . Il a également défini la spirale qui porte son nom, des formules pour les volumes de surfaces de révolution et un système ingénieux pour exprimer un très grand nombre.

Archimède est mort au cours de la Siège de Syracuse quand il a été tué par un Soldat romain en dépit des ordres qu'il ne devrait pas être affectée. Cicéron décrit visiter le tombeau d'Archimède, qui a été surmontée d'une sphère inscrite dans un cylindre. Archimède avait prouvé que la sphère a deux tiers de la superficie de volume et la surface du cylindre (y compris les bases de ce dernier), et considéré cela comme le plus grand de ses réalisations mathématiques.

Contrairement à ses inventions, les écrits mathématiques d'Archimède étaient peu connus dans l'antiquité. Mathématiciens de Alexandria lu et l'a cité, mais la première compilation exhaustive n'a été faite que c. 530 après JC par Isidore de Milet, tandis que des commentaires sur les œuvres d'Archimède écrits par Eutocius dans le sixième siècle de notre ère les ouvrit à une plus large lectorat pour la première fois. Les quelques copies de l'œuvre écrite d'Archimède qui ont survécu à travers les Moyen Age étaient une source influente d'idées pour les scientifiques au cours de la Renaissance , tandis que la découverte en 1906 des œuvres inconnues auparavant par Archimède dans le Palimpseste d'Archimède a fourni de nouvelles informations sur la façon dont il a obtenu des résultats mathématiques.

Biographie

Cette statue de bronze d'Archimède est à la Archenhold Observatoire de Berlin . Elle a été sculptée par Gerhard Thieme et dévoilé en 1972.

Archimède est né c. 287 BC dans la ville portuaire de Syracuse, en Sicile, à cette époque une auto-administration colonie Magna Graecia. La date de naissance est basé sur une déclaration du Historien grec byzantin Jean Tzétzès qu'Archimède a vécu pendant 75 ans. En L'Arénaire, Archimède donne le nom de son père comme Phidias, une astronome au sujet de laquelle on ne sait rien. Plutarque a écrit dans son Vies parallèles qu'Archimède était liée au roi Hiéron II, le prince de Syracuse. Une biographie d'Archimède a été écrit par son ami Héraclide mais ce travail a été perdu, laissant les détails de sa vie obscure. On ne sait pas, par exemple, se il a jamais mariés ou avaient des enfants. Durant sa jeunesse, Archimède peut avoir étudié dans Alexandrie , l'Egypte , où Conon de Samos et Eratosthène de Cyrène étaient contemporains. Il a évoqué Conon de Samos que son ami, tandis que deux de ses œuvres ( La méthode de théorèmes et de la mécanique Bovins problème) ont introductions adressées à Eratosthène.

Archimède est mort c. 212 au cours de la Colombie-Britannique Seconde guerre punique, romaine lorsque les forces du général Marcus Claudius Marcellus a capturé la ville de Syracuse après deux longues années de siège . Selon le compte rendu populaire donnée par Plutarque, Archimède envisageait une diagramme mathématique lorsque la ville a été capturé. Un soldat romain lui avait ordonné de venir rencontrer Marcellus générales mais il a refusé, disant qu'il devait finir de travailler sur le problème. Le soldat a été exaspéré par cela, et tué d'Archimède avec son épée. Plutarque donne également un compte moins connu de la mort d'Archimède qui suggère qu'il pourrait avoir été tué alors qu'il tentait de se rendre à un soldat romain. Selon cette histoire, Archimède transportait instruments mathématiques, et a été tué parce que le soldat a pensé qu'ils étaient des objets de valeur. Général Marcellus aurait été irrité par la mort d'Archimède, comme il lui un atout scientifique précieuse examiné et avait ordonné qu'il ne soit pas blessé.

Une sphère a 2/3 du volume et de la surface de son cylindre circonscrit. Une sphère et cylindre ont été placés sur la tombe d'Archimède à sa demande.

Les dernières paroles attribuées à Archimède sont «Ne pas déranger mes cercles" ( grec : μή μου τοὺς κύκλους τάραττε), une référence aux cercles dans le dessin mathématique qu'il était censé étudier quand elles sont perturbées par le soldat romain. Cette citation est souvent donné en latin comme " Noli turbare circulos meos, "mais il n'y a aucune preuve fiable qu'Archimède prononça ces paroles et ils ne apparaissent pas dans le récit de Plutarque.

Le tombeau d'Archimède réalisé une sculpture illustrant sa démonstration mathématique préférée, constitué d'une sphère et un cylindre de même diamètre et hauteur. Archimède avait prouvé que la zone de volume et surface de la sphère sont deux tiers de celle du cylindre y compris ses bases. En 75 avant JC, 137 années après sa mort, le Romain orateur Cicero servait questeur Sicile. Il avait entendu des histoires sur le tombeau d'Archimède, mais aucun des habitants a été en mesure de lui donner l'emplacement. Il finit par trouver la tombe près de la porte agrigentin à Syracuse, dans un état négligé et envahi par les buissons. Cicéron avait la tombe nettoyé, et a été en mesure de voir la sculpture et de lire quelques-uns des versets qui avaient été ajoutés comme une inscription. Un tombeau découvert dans une cour de l'hôtel à Syracuse dans le début des années 1960 a été prétendu être que d'Archimède, mais son emplacement est aujourd'hui inconnue.

Les versions standard de la vie d'Archimède ont été écrits longtemps après sa mort par les historiens de la Rome antique. Le compte du siège de Syracuse donnée par Polybe dans son Histoire universelle a été écrit autour de 70 années après la mort d'Archimède, et a été utilisé par la suite comme une source par Plutarque et Tite-Live. Il ne éclaire pas beaucoup d'Archimède comme une personne, et se concentre sur les machines de guerre qu'il est dit avoir construit pour défendre la ville.

Découvertes et inventions

Le principe d'Archimède

Archimède peuvent avoir utilisé son principe de flottabilité pour déterminer si la couronne d'or était moins dense que l'or solide.

Les plus connues anecdote à propos d'Archimède raconte comment il a inventé une méthode pour déterminer le volume d'un objet de forme irrégulière. Selon Vitruve, un couronne votive pour un temple avait été fait pour le roi Hiéron II, qui avait fourni pur or pour être utilisé, et Archimède a été demandé afin de déterminer si certains d'argent avait été substitué par l'orfèvre malhonnête. Archimède avait à résoudre le problème sans endommager la couronne, il ne pouvait pas le faire fondre dans un corps en forme régulièrement afin de calculer sa densité . Tout en prenant un bain, il a remarqué que le niveau de l'eau dans la baignoire se leva comme il est entré, et a réalisé que cet effet pourrait être utilisé pour déterminer le volume de la couronne. Pour des raisons pratiques l'eau est incompressible, donc la couronne immergée déplacerait une quantité d'eau égale à son propre volume. En divisant la masse de la couronne par le volume d'eau déplacé, la densité de la couronne pourrait être obtenu. Cette densité sera inférieure à celle de l'or si des métaux moins coûteux et moins denses ont été ajoutés. Archimède a ensuite pris les rues nues, tellement excité par sa découverte qu'il avait oublié de se habiller, de pleurer " Eureka! »( grec : «εὕρηκα," qui signifie "je l'ai trouvé"!) Le test a été effectué avec succès, ce qui prouve que l'argent avait bien été mélangés dans..

L'histoire de la couronne d'or ne apparaît pas dans les œuvres les plus connues d'Archimède. Par ailleurs, la pratique de la méthode qu'il décrit a été remise en question, en raison de l'extrême précision avec laquelle il faudrait mesurer le déplacement de l'eau. Archimède peut avoir lieu recherché une solution qui se appliquait le principe connu dans hydrostatique que Le principe d'Archimède, qu'il décrit dans son traité Sur corps flottants. Ce principe stipule qu'un corps plongé dans un fluide A expériences force de flottabilité égale au poids du fluide qu'il déplace. Selon ce principe, il aurait été possible de comparer la densité de la couronne d'or à celle de l'or massif en équilibrant la couronne sur une échelle avec un échantillon de référence de l'or, puis immerger l'appareil dans l'eau. La différence de densité entre les deux échantillons causerait la balance à pencher en conséquence. Galileo a jugé "probable que cette méthode est la même que d'Archimède suivie, puisque, en plus d'être très précis, il est basé sur des démonstrations trouvés par Archimède lui-même." Dans un texte du 12e siècle intitulé Mappae clavicule il ya des instructions sur la façon d'effectuer les pesées dans l'eau afin de calculer le pourcentage d'argent utilisée, et donc résoudre le problème. Le poème latin Carmen de ponderibus et mensuris de la 4ème ou 5ème siècle décrit l'utilisation d'une balance hydrostatique pour résoudre le problème de la couronne, et les attributs de la méthode à Archimède.

La vis d'Archimède

Le Vis d'Archimède peut élever l'eau efficacement.

Une grande partie des travaux d'Archimède en génie né de répondre aux besoins de sa ville natale de Syracuse. L'écrivain grec Athénée de Naucratis décrit comment le roi Hiéron II chargea d'Archimède pour concevoir un immense navire, le Syracusia, qui pourrait être utilisé pour Voyage de luxe, transportant des fournitures, et comme un navire de guerre navale. Le Syracusia est dit avoir été le plus grand navire construit dans l'Antiquité classique. Selon Athénée, il était capable de transporter 600 personnes et comprenait décorations de jardin, un gymnase et un temple dédié à la déesse Aphrodite parmi ses installations. Depuis un navire de cette taille serait une fuite d'une quantité considérable d'eau à travers la coque, la Vis d'Archimède a été prétendument développé afin d'éliminer l'eau de cale. La machine d'Archimède est un dispositif avec une lame en forme de vis tournant à l'intérieur d'un cylindre. Il a été tourné à la main, et pourrait également être utilisé pour transférer de l'eau d'un corps de basse altitude de l'eau dans les canaux d'irrigation. La vis d'Archimède est encore en usage aujourd'hui pour pomper des liquides et des solides granulés tels que le charbon et les céréales. La vis d'Archimède décrit à l'époque romaine par Vitruve a peut-être eu une amélioration sur une pompe à vis qui a été utilisé pour irriguer le Jardins suspendus de Babylone. Premier de mer au monde paquebot avec une hélice de vis était le SS Archimède, qui a été lancé en 1839 et nommé en l'honneur d'Archimède et son travail sur la vis.

Griffe d'Archimède

Le Griffe d'Archimède est une arme qu'il aurait conçue pour défendre la ville de Syracuse. Aussi connu comme "le shaker du navire," la griffe se composait d'un bras de la grue comme à partir de laquelle un grand grappin métallique a été suspendu. Lorsque la griffe a été abandonné sur un navire attaquer le bras serait balancer vers le haut, soulevant le bateau hors de l'eau et, éventuellement, de le couler. Il ya eu des expériences modernes pour tester la faisabilité de la griffe, et en 2005 un documentaire télévisé intitulé superarmes du monde antique construit une version de la griffe et a conclu que ce était un dispositif viable.

rayons thermiques

Archimède peuvent avoir utilisé des miroirs agissant collectivement comme un réflecteur parabolique de brûler navires attaquer Syracuse.

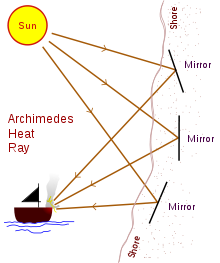
L'AD auteur 2ème siècle Lucian a écrit que pendant la Siège de Syracuse (c. 214-212 BC), Archimède détruit les navires ennemis avec le feu. Des siècles plus tard, Anthemius de Tralles mentionne brûlant lunettes que l'arme d'Archimède. Le dispositif, parfois appelé le "rayon de chaleur d'Archimède", a été utilisée pour concentrer la lumière solaire sur les navires qui approchent, les obligeant à prendre feu.

Cette arme présumée a fait l'objet de débat en cours sur sa crédibilité depuis la Renaissance. René Descartes rejetée comme fausse, tandis que les chercheurs modernes ont tenté de recréer l'effet en utilisant uniquement les moyens qui auraient été disponibles à Archimède. Il a été suggéré qu'une large gamme de poli bronze ou cuivre boucliers agissant comme des miroirs auraient été employées pour concentrer la lumière du soleil sur un bateau. Cela aurait utilisé le principe du réflecteur parabolique d'une manière similaire à un four solaire.

Un test du rayon de chaleur Archimède a été réalisée en 1973 par le savant grec Ioannis Sakkas. L'expérience a eu lieu au Base navale Skaramagas en dehors d'Athènes . A cette occasion, les miroirs 70 ont été utilisés, chacun ayant un revêtement de cuivre et d'une taille de l'ordre de cinq à trois pieds (1,5 m) par une. Les miroirs ont été signalées à un contreplaqué maquette d'un navire romain à une distance d'environ 160 pieds (50 m). Lorsque les miroirs ont porté précisément, le navire a pris feu en quelques secondes. Le navire de contreplaqué avait une couche de peinture de goudron, ce qui peut avoir assistée combustion. Un revêtement de goudron aurait été monnaie courante sur les navires dans l'ère classique.

En Octobre 2005, un groupe d'étudiants de la Massachusetts Institute of Technology a réalisé une expérience avec une 127 pieds (30 cm) des carreaux de miroir carré, porté sur un bateau en bois mock-up à une distance d'environ 100 pieds (30 m). Flames a éclaté sur un patch du navire, mais seulement après que le ciel avait été sans nuages et le navire était resté stationnaire pendant une dizaine de minutes. Il a été conclu que le dispositif était une arme possible dans ces conditions. Le groupe MIT a répété l'expérience pour l'émission de télévision MythBusters, en utilisant un bateau de pêche en bois dans San Francisco en tant que cible. Encore une fois une certaine carbonisation a eu lieu, avec une petite quantité de flamme. Afin de prendre feu, le bois doit atteindre son la température d'auto-inflammation, qui est d'environ 300 ° C (570 ° F).

Lorsque MythBusters diffusé le résultat de l'expérience de San Francisco en Janvier 2006, la demande a été placé dans la catégorie des "éclaté" (ou pas) en raison de la longueur du temps et les conditions météorologiques idéales nécessaires pour la combustion de se produire. Il a également été souligné que, depuis Syracuse face à la mer vers l'est, la flotte romaine aurait dû attaquer pendant le matin de la collecte optimale de la lumière par les miroirs. MythBusters a également souligné que les armes conventionnelles, comme des flèches enflammées ou des boulons de une catapulte, aurait été une manière beaucoup plus facile de fixer un bateau en feu sur de courtes distances.

En Décembre 2010, MythBusters regarda de nouveau l'histoire des rayons de chaleur dans une édition spéciale avec Barack Obama , Défi intitulé président. Plusieurs expériences ont été réalisées, y compris un essai grande échelle avec 500 écoliers visant miroirs à une maquette d'un voilier Roman 400 pieds (120 m) de distance. Dans toutes les expériences, la voile a échoué à atteindre les 210 ° C (410 ° F) nécessaire pour prendre feu, et le verdict était à nouveau "éclaté". Le spectacle a conclu qu'un effet plus probable des miroirs aurait été aveugle, éblouissant, ou distraire l'équipage du navire.

Autres découvertes et inventions

Alors que d'Archimède n'a pas inventé le levier, il a donné une explication du principe impliqué dans son travail sur l'équilibre de Planes. Descriptions antérieures du levier se trouvent dans la École péripatéticienne des adeptes de Aristote , et sont parfois attribué à Archytas. Selon Pappus d'Alexandrie, le travail d'Archimède sur des leviers lui a fait la remarque: «Donnez-moi un point d'appui, et je soulèverai le monde." ( grec : δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω) Plutarque décrit comment Archimède conçus bloc-et-attaquer systèmes de poulies, permettant aux marins utilisent le principe de levier pour soulever des objets qui auraient autrement été trop lourd à déplacer. Archimède a également été crédité de l'amélioration de la puissance et la précision de la catapulte, et d'inventer le odomètre au cours de la Première Guerre punique. Le compteur kilométrique a été décrit comme un panier avec un mécanisme d'engrenage qui a chuté d'une balle dans un récipient après chaque mile parcouru.

Cicéron (106-43 avant JC) mentionne brièvement Archimède dans son dialogue De Republica, qui met en scène une conversation fictive prenant place dans 129 BC. Après la prise de Syracuse c. 212 BC, le général Marcus Claudius Marcellus aurait repris à Rome deux mécanismes, construits par Archimède et utilisées en tant qu'auxiliaires de l'astronomie, qui a montré le mouvement du Soleil, la Lune et cinq planètes. Cicéron mentionne des mécanismes similaires conçus par Thalès de Milet et Eudoxe de Cnide. Le dialogue dit que Marcellus a gardé un des dispositifs que son seul butin personnelle de Syracuse, et a fait don de l'autre au temple des Vertus à Rome. Le mécanisme de Marcellus a été démontré, selon Cicéron, par Gaius Sulpicius Gallus Lucius Furius Philus, qui l'a décrit ainsi:

Hanc sphaeram Gallus cum moveret, fiebat ut soli luna totidem conversionibus dans aere illo quot diebus dans ipso caelo succederet, ex quo et dans caelo sphaera solis Fieret eadem illa defectio, et incideret luna tum dans eam métam quae esset umbra terrae, cum Sol e regione . - Lorsque Gallus déplacé le monde, il est arrivé que la Lune a suivi le Sun par autant de tours sur ce bronze artifice que dans le ciel lui-même, à partir de laquelle aussi dans le ciel le globe du soleil devint d'avoir la même éclipse, et la Lune est alors venue à ce poste qui était son ombre sur la Terre, lorsque le Soleil est en ligne.

Ce est une description d'un un planétarium ou orrery. Pappus d'Alexandrie a déclaré que Archimède avait écrit un manuscrit (maintenant perdu) sur la construction de ces mécanismes intitulé Sur Sphère de décision. La recherche moderne dans ce domaine a été axée sur la Mécanisme d'Anticythère, un autre appareil de l'antiquité classique qui a probablement été conçu pour le même but. Mécanismes de ce genre, il aurait fallu construire une connaissance sophistiquée de engrenage différentiel. Cela a été une fois pensé pour avoir été au-delà de la portée de la technologie disponible dans les temps anciens, mais la découverte du mécanisme d'Anticythère en 1902 a confirmé que les dispositifs de ce genre étaient connus des anciens Grecs.

Mathématiques

Alors qu'il est souvent considéré comme un concepteur de dispositifs mécaniques, Archimède a également fait contributions dans le domaine des mathématiques. Plutarque écrit: "Il a mis toute son affection et son ambition dans ces spéculations pures où il peut y avoir aucune référence aux besoins vulgaires de la vie."

Archimède utilisé le théorème de Pythagore pour calculer le côté de la 12-gone de celle de l' hexagone et pour chaque doublement ultérieure des côtés du polygone régulier.

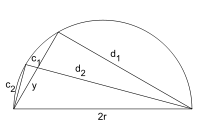
Archimède a pu utiliser infinitésimales d'une manière qui est similaire au moderne calcul intégral . Grâce à la preuve par l'absurde ( reductio ad absurdum), il pourrait donner des réponses à des problèmes à un degré de précision arbitraire, tout en précisant les limites dans lesquelles la réponse Lay. Cette technique est connue sous le nom méthode de l'épuisement, et il employait pour estimer la valeur de π. En De la mesure du cercle il a fait cela en dessinant un grand hexagone régulier en dehors d'un cercle et un hexagone régulier plus petit à l'intérieur du cercle, et de doubler progressivement le nombre de côtés de chaque polygone régulier, le calcul de la longueur d'un côté de chaque polygone à chaque étape. Comme le nombre de côtés augmente, il devient une approximation plus précise de cercle. Après quatre telles mesures, lorsque les polygones avaient 96 parties chacun, il a pu déterminer que la valeur de π se trouvait entre 3 _^1/7 (environ 3,1429) et 3 _^10/71 (environ 3,1408), conformément à sa valeur réelle d'environ 3,1416. Il a aussi prouvé que la zone d'un cercle était égale à π multipliée par le carré de la rayon du cercle (πr ^2). En Sur la sphère et du cylindre, Archimède postule que toute grandeur lorsqu'il est ajouté à lui-même suffisamment de fois dépasseront toute grandeur donnée. Ceci est le Archimédien des nombres réels.

En De la mesure du cercle, Archimède donne la valeur de la racine carrée de trois comme se situant entre _^265/153 (environ 1,7320261) et _^1351/780 (environ 1,7320512). La valeur réelle est d'environ 1.7320508, ce qui en fait une estimation très précise. Il a présenté ce résultat sans offrir aucune explication de la façon dont il l'avait obtenu. Cet aspect de l'œuvre d'Archimède causé John Wallis faire remarquer qu'il était: «que ce était à dessein d'avoir couvert les traces de son enquête comme se il avait envié la postérité le secret de sa méthode d'enquête alors qu'il voulait leur extorquer assentiment à ses résultats." Il est possible qu'il utilise une procédure itérative pour calculer ces valeurs.

Comme prouvé par Archimède, la zone de la segment de parabole dans la figure supérieure est égale à 4/3 celle du triangle inscrit dans le chiffre le plus bas.

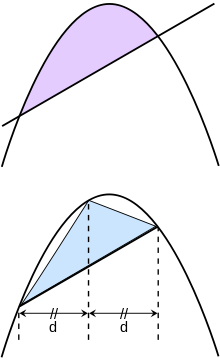
En La Quadrature de la parabole, Archimède se est avéré que la surface délimitée par un parabole et une ligne droite est _^4/3 fois la superficie d'un correspondant inscrit triangle comme indiqué dans la figure de droite. Il a exprimé la solution au problème comme une infini série géométrique avec le rapport commun _^1/4:

Si le premier terme de cette série est l'aire du triangle, puis la seconde est la somme des aires des deux triangles dont les bases sont les deux plus petits lignes sécantes, et ainsi de suite. Cette preuve utilise une variante de la série 1/4 + 1/16 + 1/64 + + 1/256 · · · qui résume à ^{_un tiers.}

En L'Arénaire, Archimède a entrepris de calculer le nombre de grains de sable que l'univers pourrait contenir. Ce faisant, il a défié la notion que le nombre des grains de sable est trop grand pour être comptés. Il a écrit: «Il ya certains, roi Gelo (Gelo II, fils de Hiéron II), qui pensent que le nombre de le sable est infini dans la multitude; et je veux dire par le sable non seulement ce qui existe à propos de Syracuse et le reste de la Sicile, mais aussi celle qui se trouve dans toutes les régions habitées ou si inhabitée. "Pour résoudre le problème, Archimède a conçu un système de comptage fondé sur le multitude. Le mot est de la μυριάς murias grec, pour le nombre 10 000. Il a proposé un système de numération utilisant les pouvoirs d'une myriade de myriades (100 millions) et a conclu que le nombre de grains de sable nécessaires pour remplir l'univers serait 8 vigintillion, ou 8 × 10 ^63.

Écrits

Les travaux d'Archimède ont été écrites en Grec dorique, le dialecte de l'ancienne Syracuse. Le travail écrit d'Archimède n'a pas survécu ainsi que celle de Euclid , et sept de ses traités sont connus pour avoir existé que par des références qui leur sont faites par d'autres auteurs. Pappus d'Alexandrie mentionne Sur Sphère de décision et un autre ouvrage sur les polyèdres , tandis que Théon d'Alexandrie cite une remarque à propos réfraction de la Catoptrica maintenant perdu. Durant sa vie, Archimède fait connaître par correspondance avec les mathématiciens dans son travail d'Alexandrie . Les écrits d'Archimède ont été recueillies par le byzantine architecte Isidore de Milet (c. 530 AD), tandis que des commentaires sur les œuvres d'Archimède écrits par Eutocius au sixième siècle AD a contribué à faire son travail un plus large public. Le travail d'Archimède a été traduit en arabe par Thābit ibn Qurra (836-901 AD), et le latin par Gérard de Crémone (c. 1114-1187 AD). Pendant la Renaissance , l'édition princeps (première édition) a été publié dans de Bâle en 1544 par Johann Herwagen avec les œuvres d'Archimède en grec et en latin. Autour de l'an 1586 Galileo Galilei a inventé un équilibre hydrostatique pour peser les métaux dans l'air et de l'eau après avoir apparemment été inspiré par le travail d'Archimède.

Survivre œuvres

Archimède est dit avoir remarqué de la levier: Donnez-moi un point d'appui, et je soulèverai le monde.

• Sur l'équilibre de Planes (deux volumes)

Le premier livre est dans une quinzaine de propositions avec sept postule, tandis que le second livre est en dix propositions. Dans ce travail d'Archimède explique la Loi du levier, en déclarant: «Les magnitudes sont en équilibre à des distances réciproquement proportionnelles à leur poids."

Archimède utilise les principes dérivés pour calculer les zones et les centres de gravité des différentes figures géométriques, y compris des triangles , parallélogrammes et paraboles.

• Sur la mesure d'un cercle

Ce est un petit ouvrage composé de trois propositions. Il est écrit sous la forme d'une correspondance avec Dosithée de Péluse, qui était un élève de Conon de Samos. Dans la proposition II, Archimède donne un approximation de la valeur de pi (π), ce qui montre qu'il est supérieur à _^223/71 et inférieur à _^22/7.

• Sur Spirales

Ce travail de 28 propositions se adresse également à Dosithée. Le traité définit ce qui est maintenant appelé le Spirale d'Archimède. C'est le lieu des points correspondant aux emplacements dans le temps d'un point se éloigner d'un point fixe avec une vitesse constante le long d'une ligne qui tourne avec une constante de vitesse angulaire . De manière équivalente, en coordonnées polaires (r, θ), il peut être décrit par l'équation

avec des nombres réels a et b. Ce est un des premiers exemples d'une courbe mécanique (une courbe tracée par un déplacement points) examinée par un mathématicien grec.

• Sur la sphère et le cylindre (deux volumes)

Dans ce traité, adressée à Dosithée, Archimède obtient le résultat dont il était le plus fier, à savoir la relation entre une sphère et un circonscrit cylindre de même hauteur et de diamètre . Le volume est _^4/3 π r ³ de la sphère, et 2 π r ³ pour le cylindre. La surface spécifique est de 4 π r ² pour la sphère, et 6 π r ² pour le cylindre (y compris ses deux bases), où r est le rayon de la sphère et le cylindre. La sphère a un volume deux tiers de celle du cylindre circonscrit. De même, la sphère a une superficie deux tiers de celle du cylindre (y compris les bases). Une sphère sculpté et le cylindre ont été placés sur la tombe d'Archimède à sa demande.

• Sur conoïdes et Sphéroïdes

Ce est un travail en 32 propositions adressées Dosithée. Dans ce traité d'Archimède calcule les surfaces et les volumes de sections de cônes, des sphères et paraboloïdes.

• Le corps flottants (deux volumes)

Dans la première partie de ce traité, Archimède énonce la loi de l'équilibre des fluides, et prouve que l'eau va adopter une forme sphérique autour d'un centre de gravité. Cela peut avoir été une tentative d'expliquer la théorie des astronomes grecs contemporains tels que Eratosthène que la Terre est ronde. Les fluides décrits par Archimède ne sont pas auto-gravitant, car il suppose l'existence d'un point vers lequel toutes les choses tombent afin d'obtenir la forme sphérique.

Dans la deuxième partie, il calcule les positions des sections de paraboloïdes d'équilibre. Ce était probablement une idéalisation des formes de la coque des navires. Certains de ses sections flottent avec la base sous l'eau et le sommet au-dessus de l'eau, semblable à la façon dont les icebergs flottent. Le principe d'Archimède de la flottabilité est donnée dans l'ouvrage, a déclaré ce qui suit:

Tous les corps totalement ou partiellement immergé dans un fluide expériences égal à une poussée vers le haut, mais de sens opposé à, le poids du fluide déplacé.

• La Quadrature de la parabole

Dans ce travail de 24 propositions adressées à Dosithée, Archimède prouve par deux méthodes que la surface délimitée par un parabole et une ligne droite est 4/3 multiplié par la surface d'un triangle avec la même base et la hauteur. Il y parvient en calculant la valeur d'une série géométrique qui résume à l'infini avec le rapport _^1/4.

• (O) Stomachion

C'est un dissection de puzzle semblable à un Tangram, et le traité décrivant il a été constaté sous une forme plus complète dans le Palimpseste d'Archimède. Archimède calcule les zones des 14 pièces qui peuvent être assemblés pour former un carré . Une recherche publiée par le Dr Reviel Netz des Université de Stanford en 2003 a fait valoir que d'Archimède tentait de déterminer combien de façons les pièces pourraient être assemblés en la forme d'un carré. Dr Netz calcule que les pièces peuvent être faites dans un carré 17152 façons. Le nombre d'accords est 536 lorsque des solutions qui sont équivalentes par la rotation et la réflexion ont été exclus. Le puzzle représente un exemple d'un problème au début de la combinatoire .

L'origine du nom de l'énigme ne est pas claire, et il a été suggéré que ce est tiré du grec ancien mot pour la gorge ou l'œsophage, stomachos (στόμαχος). Ausone se réfère à l'énigme que Loculus d'Archimède, un mot composé grec formé à partir des racines de ὀστέον (osteon, os) et μάχη (Mâche - combat). Le casse-tête est également connu comme les Loculus d'Archimède ou Box Archimède.

• Problème des bœufs d'Hélios

Ce travail a été découvert par Gotthold Ephraim Lessing dans un manuscrit grec consistant en un poème de 44 lignes, à la Bibliothèque Herzog Août dans Wolfenbüttel, Allemagne en 1773. Elle est adressée à Eratosthène et les mathématiciens à Alexandrie. Archimède les met au défi de compter le nombre de bovins dans le troupeau du Soleil par la résolution d'un certain nombre de simultanée Équations diophantiennes. Il existe une version plus difficile du problème dans lequel certaines des réponses doivent être nombres carrés. Cette version du problème a été résolu par A. Amthor en 1880, et la réponse est un très grand nombre, environ 7,760271 × 10 ^{206 544.}

• L'Arénaire

Dans ce traité, Archimède compte le nombre de grains de sable qui se adaptera à l'intérieur de l'univers. Ce livre mentionne le héliocentrique théorie du système solaire proposé par Aristarque de Samos, ainsi que des idées contemporaines sur la taille de la Terre et la distance entre les différents corps célestes. En utilisant un système de numéros sur la base de compétences de la multitude, Archimède conclut que le nombre de grains de sable nécessaire pour remplir l'univers est de 8 × 10 ⁶³ en notation moderne. La lettre d'introduction stipule que le père d'Archimède était un astronome du nom de Phidias. L'Arénaire ou Psammites est le seul travail survivre dans lequel Archimède parle de ses vues sur l'astronomie.

• Traité de la Méthode

Ce traité a été pensé perdu jusqu'à la découverte de la Palimpseste d'Archimède en 1906. Dans ce travail utilise Archimède infinitésimales, et montre comment briser un chiffre dans un nombre infini de parties infiniment petites peuvent être utilisés pour déterminer sa surface ou de volume. Archimède ont pu considérer cette méthode manque de rigueur formelle, donc il a aussi utilisé le méthode de l'épuisement pour dériver les résultats. Comme le problème du bétail, Traité de la Méthode a été écrit sous la forme d'une lettre à Eratosthène en Alexandrie .

Œuvres apocryphes

Archimède Livre de lemmes ou Liber Assumptorum est un traité avec quinze propositions sur la nature des cercles. La copie la plus ancienne connue du texte est en arabe . Les chercheurs TL et Heath Marshall Clagett a fait valoir qu'il ne peut pas avoir été écrite par Archimède dans sa forme actuelle, car il cite Archimède, suggérant la modification par un autre auteur. Le lemmes peut être basée sur un travail antérieur par Archimède qui est maintenant perdu.

Il a également été dit que La formule de Heron pour calculer la superficie d'un triangle à partir de la longueur de ses côtés était connu Archimède.Cependant, la première référence fiable pour la formule est donnée parHéron d'Alexandrie dans le 1er siècle après JC.

Palimpseste d'Archimède

Stomachionest uncasse-tête de dissection dans lepalimpseste d'Archimède.

Le document contenant tout le travail d'Archimède est le palimpseste d'Archimède. En 1906, le professeur danois Johan Ludvig Heiberg a visité Constantinople et a examiné un de 174 pages de parchemin en peau de chèvre de prières écrites dans le 13ème siècle. Il a découvert qu'il était un palimpseste, un document avec le texte qui avait été écrit sur ​​un travail plus ancien effacé. Palimpsestes ont été créés en grattant l'encre d'œuvres existantes et la réutilisation eux, ce qui était une pratique courante dans le Moyen Age comme vélin était cher. Les œuvres plus anciennes dans le palimpseste ont été identifiés par les chercheurs comme 10e siècle AD copies de traités précédemment inconnus par Archimède. Le parchemin a passé des centaines d'années dans une bibliothèque du monastère de Constantinople avant d'être vendu à un collectionneur privé dans les années 1920. Le 29 Octobre 1998, il a été vendu aux enchères à un acheteur anonyme pour 2 millions de dollars à Christie à New York . Le palimpseste détient sept traités, y compris la seule copie survivante de Sur corps flottants dans l'original grec. Il est la seule source connue de Traité de la Méthode , évoquée par Suidas et qui aurait été perdu à jamais. Stomachion a également été découvert dans le palimpseste, avec une analyse plus complète du puzzle que ce qui avait été trouvé dans les textes précédents. Le palimpseste est maintenant enregistrée à la Walters Art Museum de Baltimore, Maryland, où il a été soumis à une série de tests modernes, y compris l'utilisation de rayons ultraviolets et des rayons X de lumière pour lire le texte remplacé.

Les traités dans le palimpseste d'Archimède sont:sur l'équilibre des Planes, Des spirales, de la mesure du cercle, sur la sphère et le cylindre, Le corps flottants, Traité de la MéthodeetStomachion.

Héritage

Le Médaille Fields porte un portrait d'Archimède.

• Il y a un cratère sur la Lune nommé Archimède (29,7 ° N, 4.0 ° W) en son honneur, ainsi que toute une gamme lunaire de montagne, laMontes Archimède (25,3 ° N, 4.6 ° W).
• L'astéroïde 3600 Archimède est nommé d'après lui.
• Le Médaille Fields pour ses réalisations exceptionnelles en mathématiques porte un portrait d'Archimède, avec une sculpture illustrant sa preuve sur la sphère et le cylindre. L'inscription autour de la tête d'Archimède est une citation attribuée à lui qui se lit en latin: "Transire suum pectus mundoque potiri" (Lève-dessus de soi et de saisir le monde).
• Archimède est apparu sur les timbres émis parl'Allemagne de l'Est (1973),la Grèce(1983),l'Italie(1983),le Nicaragua(1971),Saint-Marin(1982), etl'Espagne(1963).
• L'exclamation de Eureka! attribué à Archimède est la devise de l'état de Californie . Dans ce cas, le mot renvoie à la découverte d'or près de Mill de Sutter en 1848, qui a déclenché la California Gold Rush.
• Un mouvement pour l'engagement civique visant l'accès universel aux soins de santé dans l'État américain del'Oregona été nommé le "Mouvement d'Archimède», dirigé par l'ancien gouverneur de l'OregonJohn Kitzhaber.

Les travaux d'Archimèdeen ligne

• Texte en grec classique:scans PDF de l'édition Heiberg des œuvres d'Archimède, maintenant dans le domaine public
• Dans la traduction anglaise: Les Travaux d'Archimède , trans. TL Heath; complétée par Traité de la Méthode , trans. LG Robinson