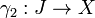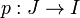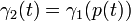Courbe
Renseignements généraux
Cette sélection de wikipedia a été choisi par des bénévoles aidant les enfants SOS de Wikipedia pour cette sélection Wikipedia pour les écoles. Mères SOS chaque regard après une une famille d'enfants parrainés .
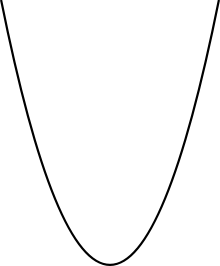
En mathématiques , une courbe (aussi appelé une ligne courbe dans les textes anciens) est, de manière générale, un objet semblable à une ligne mais qui ne est pas nécessaire d'être tout droit. Cela implique qu'une ligne est un cas particulier de la courbe, à savoir une courbe avec null courbure. Souvent, dans les courbes en deux dimensions ( courbes planes) ou en trois dimensions (courbes spatiales) espace euclidien sont d'intérêt.
Diverses disciplines dans les mathématiques ont donné le terme des significations différentes en fonction de la zone d'étude, de sorte que le sens précis dépend du contexte. Cependant, bon nombre de ces significations sont des cas particuliers de la définition qui suit. Une courbe est un espace topologique qui est localement homéomorphe à une ligne. Dans le langage courant, cela signifie que la courbe est un ensemble de points qui, à proximité de chacun de ses points, ressemble à une ligne, jusqu'à une déformation. Un exemple simple d'une courbe est la parabole, indiqué à droite. Un grand nombre d'autres courbes ont été étudiés dans des domaines multiples et mathématiques.
La courbe terme a plusieurs significations en langue non-mathématique ainsi. Par exemple, il peut être presque synonyme de fonction mathématique (comme dans courbe d'apprentissage), ou graphique d'une fonction (comme dans Courbe de Phillips).
Une arc ou un segment de courbe est une partie d'une courbe qui est délimité par deux points d'extrémité distinctes et contient tous les points de la courbe entre ses points d'extrémité. Selon la manière dont l'arc est définie, l'un des deux points d'extrémité peuvent ou non faire partie de celui-ci. Lorsque l'arc est droite, il est généralement appelé segment de ligne.
Histoire

Fascination avec des courbes a commencé longtemps avant qu'ils ont fait l'objet d'étude mathématique. Ceci peut être vu dans de nombreux exemples de leur usage décoratif dans l'art et sur les objets du quotidien datant de la préhistoire. Courbes, ou tout au moins leurs représentations graphiques, sont simples à créer, par exemple par un bâton dans le sable sur une plage.
Historiquement, le terme «ligne» a été utilisé à la place du terme "courbe" plus moderne. Par conséquent, les expressions «ligne droite» et «ligne droite» ont été utilisés pour distinguer ce qui est appelé aujourd'hui les lignes de "lignes courbes». Par exemple, dans le livre I des Éléments d'Euclide , une ligne est définie comme une "longueur sans largeur" (Def. 2), tandis qu'une ligne droite est définie comme «une ligne qui est également placée entre les points sur elle-même» (Def. 4) . L'idée d'Euclide d'une ligne est peut-être clarifié par la déclaration "Les extrémités d'une ligne sont des points," (Def. 3). Commentateurs ultérieurs classées en outre des lignes selon les différents régimes. Par exemple:
- Lignes composites (lignes formant un angle)
- Lignes Incomposite
- Déterminé (lignes qui ne se étendent pas indéfiniment, telles que le cercle)
- Indéterminée (lignes qui se étendent indéfiniment, comme la ligne droite et la parabole)
Le Grec géomètres avaient étudié de nombreux autres types de courbes. Une raison était de leur intérêt pour la résolution de problèmes géométriques qui ne pouvaient être résolus en utilisant la norme règle et au compas construction. Ces courbes sont les suivants:
- Les sections coniques , profondément étudiées par Apollonius de Perge
- Le cissoïde de Dioclès, étudiée par Dioclès et utiliser une méthode pour doubler le cube.
- Le conchoïde de Nicomède, étudiée par Nicomedes comme méthode à la fois à deux fois le cube et à trisecter un angle.
- Le Spirale d'Archimède, étudié par Archimède comme une méthode pour trisecter un angle et la quadrature du cercle.
- Le Spiric sections, sections de tores étudiés par Persée que des sections de cônes avait été étudié par Apollonius.

Une avancée fondamentale dans la théorie des courbes était l'avènement de la géométrie analytique au XVIIe siècle. Cela a permis une courbe à être décrit par une équation plutôt que d'une construction géométrique complexe. Ce permis non seulement de nouvelles courbes à définir et étudié, mais il a permis une distinction formelle à faire entre les courbes qui peuvent être définis à l'aide équations algébriques, courbes algébriques, et ceux qui ne peuvent pas, courbes transcendantes. Auparavant, les courbes ont été décrits comme «géométrique» ou «mécanique», selon la façon dont ils étaient ou pourraient être supposément, générés.
Sections coniques ont été appliquées dans l'astronomie par Kepler . Newton a également travaillé sur un exemple précoce dans le calcul des variations . Les solutions aux problèmes de variations, comme le brachistochrone et questions tautochrone, propriétés introduites de courbes dans de nouvelles façons (dans ce cas, le cycloïde). Le caténaire tire son nom comme la solution au problème d'une chaîne de suspension, le genre de question qui est devenue régulièrement accessible par des moyens de le calcul différentiel.
Au XVIIIe siècle vinrent les débuts de la théorie des courbes planes algébriques, en général. Newton avait étudié la cubiques, dans la description générale des points réels en «ovales». La déclaration de Théorème de Bézout a montré un certain nombre d'aspects qui ne étaient pas directement accessibles à la géométrie de l'époque, à voir avec les points singuliers et des solutions complexes.
Dès le XIXe siècle, il ne est pas une théorie de la courbe séparée, mais plutôt l'apparence de courbes que l'aspect unidimensionnel de la géométrie projective, et la géométrie différentielle ; et par la suite la topologie , lorsque par exemple la Théorème de Jordan a été entendu à mentir assez profond, ainsi que d'être requis dans analyse complexe. L'ère de la courbe l'espace-remplissage finalement provoqué les définitions modernes de la courbe.
Topologie
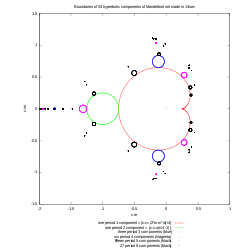
Dans la topologie , une courbe est définie comme suit. Laisser 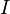 être un intervalle de nombres réels (c.-à-un non vide relié sous-ensemble de
être un intervalle de nombres réels (c.-à-un non vide relié sous-ensemble de 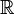 ). Ensuite, une courbe
). Ensuite, une courbe 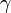 est un continu cartographie
est un continu cartographie 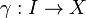 Où
Où 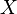 est un espace topologique.
est un espace topologique.
- La courbe
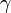 est dit être simple, ou un arc Jordanie, se il est injective, ce est à dire si pour tout
est dit être simple, ou un arc Jordanie, se il est injective, ce est à dire si pour tout  ,
,  en
en 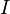 , Nous avons
, Nous avons 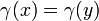 implique
implique  . Si
. Si 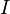 est un intervalle fermé borné
est un intervalle fermé borné ![\, \! [A, b]](../../images/2348/234806.png) , Nous permettons aussi la possibilité
, Nous permettons aussi la possibilité 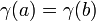 (Cette convention permet de parler de courbes simples «fermés», voir ci-dessous).
(Cette convention permet de parler de courbes simples «fermés», voir ci-dessous).
En d'autres termes cette courbe "ne se croisent pas et n'a pas de points manquants".
- Si
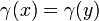 pour certains
pour certains  (Autres que les extrémités de
(Autres que les extrémités de 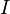 ), Puis
), Puis 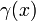 est appelé un point double (ou multiple) de la courbe.
est appelé un point double (ou multiple) de la courbe.
- Une courbe
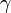 est dit être fermé ou si une boucle
est dit être fermé ou si une boucle ![\, \! I = [a, b]](../../images/2348/234811.png) et si
et si 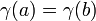 . Une courbe fermée est donc une application continue du cercle
. Une courbe fermée est donc une application continue du cercle 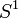 ; une courbe fermée simple est également appelée courbe de Jordan. Le Théorème de Jordan indique que ces courbes divisent le plan en un «intérieur» et «extérieur».
; une courbe fermée simple est également appelée courbe de Jordan. Le Théorème de Jordan indique que ces courbes divisent le plan en un «intérieur» et «extérieur».
Un courbe plane est une courbe pour lesquels X est le plan euclidien -Ce sont les exemples les premier rencontrées ou dans certains cas, la plan projectif. Une courbe de l'espace est une courbe pour laquelle X est de trois dimensions, généralement l'espace euclidien ; une courbe gauche est une courbe de l'espace qui se trouve dans aucun plan. Ces définitions se appliquent également à courbes algébriques (voir ci-dessous). Toutefois, dans le cas des courbes algébriques, il est très fréquent de considérer les systèmes numériques plus générale que les réels.
Cette définition de la courbe capte notre notion intuitive d'une courbe comme une figure géométrique connecté, continu qui est "similaire" une ligne, sans épaisseur et tiré sans interruption, même se il comprend également des chiffres qui peuvent difficilement être appelés courbes d'usage courant. Par exemple, l'image d'une courbe peut couvrir un carré dans le plan ( courbe de remplissage d'espace). L'image de la courbe de simple plan peut avoir Hausdorff dimension plus grande que l'un (voir Flocon de Koch) et même positif Mesure de Lebesgue (le dernier exemple peut être obtenu par la faible variation de Peano courbe construction). Le courbe dragon est un autre exemple inhabituel.
Conventions et terminologie
La distinction entre une courbe et son l'image est importante. Deux courbes distinctes peuvent avoir la même image. Par exemple, un segment de droite peut être tracée en oeuvre à des vitesses différentes, ou un cercle peut être déplacé d'un nombre différent de fois. Plusieurs fois, cependant, nous sommes seulement intéressés à l'image de la courbe. Il est important de prêter attention au contexte et de congrès de lecture.
La terminologie est également pas uniforme. Souvent, topologues utilisent le terme " chemin "pour ce que nous appelons une courbe, et" courbe "pour ce que nous appelons l'image d'une courbe. Le terme" courbe "est plus fréquente dans le calcul vectoriel et de géométrie différentielle .
Les longueurs des courbes
Si 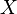 est un espace métrique avec métrique
est un espace métrique avec métrique 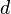 , Alors nous pouvons définir la longueur d'une courbe
, Alors nous pouvons définir la longueur d'une courbe ![! \ \, \ Gamma: [a, b] \ rightarrow X](../../images/2348/234813.png) par
par
où le sup est sur toutes 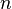 et toutes les partitions
et toutes les partitions 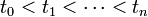 de
de ![[A, b]](../../images/2348/234816.png) .
.
Une courbe rectifiable est une courbe avec longueur finie. Un paramétrisation des 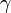 est appelé (vitesse ou unité ou paramétrée par la longueur d'arc) naturelle si, pour quelque
est appelé (vitesse ou unité ou paramétrée par la longueur d'arc) naturelle si, pour quelque 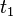 ,
, 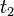 en
en ![[A, b]](../../images/2348/234816.png) , Nous avons
, Nous avons
Si 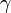 est un Fonction Lipschitz continue, alors il est automatiquement rectifiable. De plus, dans ce cas, on peut définir la vitesse (ou dérivé métrique) des
est un Fonction Lipschitz continue, alors il est automatiquement rectifiable. De plus, dans ce cas, on peut définir la vitesse (ou dérivé métrique) des 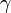 à
à 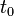 comme
comme
et puis
En particulier, si 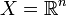 est un espace euclidien et
est un espace euclidien et ![\ Gamma: [a, b] \ rightarrow \ mathbb {R} ^ n](../../images/2348/234823.png) est différentiable alors
est différentiable alors
Géométrie différentielle
Alors que les premiers exemples de courbes que l'on rencontre sont pour la plupart courbes planes (ce est, dans les mots de tous les jours, des lignes courbes dans l'espace à deux dimensions), il ya des exemples évidents tels que la hélice qui existent naturellement dans les trois dimensions. Les besoins de la géométrie, mais aussi par exemple la mécanique classique sont d'avoir une notion de la courbe dans l'espace d'un nombre quelconque de dimensions. Dans la relativité générale , une ligne de monde est une courbe dans l'espace-temps.
Si 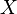 est un variété différentiable, alors nous pouvons définir la notion de courbe différentiable
est un variété différentiable, alors nous pouvons définir la notion de courbe différentiable 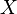 . Cette idée générale est suffisant pour couvrir la plupart des applications de courbes en mathématiques. D'un point de vue local, on peut prendre
. Cette idée générale est suffisant pour couvrir la plupart des applications de courbes en mathématiques. D'un point de vue local, on peut prendre 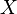 d'être l'espace euclidien . D'autre part, il est utile d'être plus générale, en ce que (par exemple), il est possible de définir le vecteurs tangents à
d'être l'espace euclidien . D'autre part, il est utile d'être plus générale, en ce que (par exemple), il est possible de définir le vecteurs tangents à 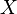 au moyen de cette notion de courbe.
au moyen de cette notion de courbe.
Si 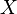 est un variété lisse, une courbe lisse
est un variété lisse, une courbe lisse 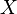 est un carte lisse
est un carte lisse
Ce est une notion fondamentale. Il ya des idées moins et plus restreints, aussi. Si 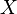 est un
est un  collecteur (ce est à dire, un collecteur dont cartes sont
collecteur (ce est à dire, un collecteur dont cartes sont  fois continûment différentiable), puis un
fois continûment différentiable), puis un  courbe en
courbe en 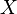 est une courbe qui est seulement supposé être
est une courbe qui est seulement supposé être  (C.
(C.  fois continûment différentiable). Si
fois continûment différentiable). Si 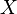 est une variété analytique (ce est à dire infiniment différentiables et les graphiques sont exprimable en série de puissance ), et
est une variété analytique (ce est à dire infiniment différentiables et les graphiques sont exprimable en série de puissance ), et 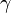 est une carte analytique, puis
est une carte analytique, puis 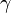 est dit être une courbe analytique.
est dit être une courbe analytique.
Une courbe différentiable est dite régulière si son dérivé ne se annule jamais. (En mots, une courbe régulière ne ralentit jamais à un arrêt ou revient en arrière sur lui-même.) Deux  courbes différentiables
courbes différentiables
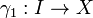 et
et
sont dites équivalentes se il existe un bijective  carte
carte
de telle sorte que la carte inverse
est aussi  Et
Et
pour tous 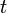 . La carte
. La carte 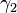 est appelé un reparamétrisation de
est appelé un reparamétrisation de  ; ce qui rend une relation d'équivalence sur l'ensemble de tous
; ce qui rend une relation d'équivalence sur l'ensemble de tous  courbes différentiables dans
courbes différentiables dans 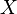 . Un
. Un  est un arc classe d'équivalence de
est un arc classe d'équivalence de  courbes sous le rapport de reparamétrisation.
courbes sous le rapport de reparamétrisation.
Courbe algébrique
Courbes algébriques sont les courbes considérées dans géométrie algébrique. Une courbe algébrique plane est le lieu des points de coordonnées x, y telles que f (x, y) = 0, où f est un polynôme à deux variables définies sur un domaine C. La géométrie algébrique regarde normalement non seulement sur des points de coordonnées par F, mais sur tous les points de coordonnées dans un corps algébriquement clos K. Si C est une courbe définie par un polynôme avec des coefficients f par F, la courbe est définie sur ledit C. Les points de la courbe C de coordonnées dans un champ G sont dits rationnel sur G et peuvent être notées C (G)); ainsi la pleine courbe C = C (K).
Courbes algébriques peuvent également être courbes spatiales, ou des courbes en dimension encore plus élevé, obtenu comme l'intersection (solution de consigne de courant) de plus d'une équation polynomiale à plus de deux variables. En éliminant les variables (par ne importe quel outil de la théorie d'élimination), une courbe algébrique peut être projetée sur un courbe algébrique plane, qui peuvent toutefois introduire de nouvelles singularités telles que cuspides ou le double de points.
Une courbe plane peut également peut également être réalisée en une courbe dans le plan projectif: si une courbe est définie par un polynôme f de degré d totale, puis d w f (u / w, v / p) à une simplifie g polynôme homogène (u, v, w) de degré d. Les valeurs de u, v, w telle que g (u, v, w) = 0 sont les coordonnées homogènes des points de l'achèvement de la courbe dans le plan projectif et les points de la courbe initiale sont ceux tels w est pas zéro. Un exemple est le Fermat courbe u n + v n = w n, qui a une forme affine x n + y n = 1. Un processus similaire d'homogénéisation peut être défini pour les courbes dans des espaces de dimensions supérieures
Des exemples importants de courbes algébriques sont les coniques , qui sont non singulières courbes de degré deux et genre zéro et elliptiques courbes , qui sont courbes non singulières du genre une étudié dans la théorie des nombres et qui ont des applications importantes pour la cryptographie . Comme les courbes algébriques dans les domaines de le plus souvent caractéristique zéro sont étudiés au cours des nombres complexes , courbes algébriques en géométrie algébrique peuvent être considérés comme de véritables surfaces. En particulier, les courbes algébriques projectives complexes non-singuliers sont appelées surfaces de Riemann .
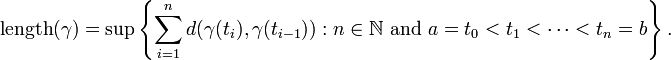
![\ Text {longueur} (\ gamma | _ {[t_1, t_2]}) = | t_2-t_1 |.](../../images/2348/234819.png)