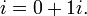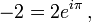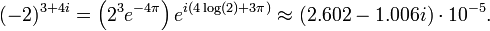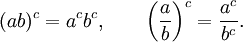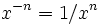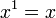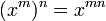Exponentiation
Renseignements généraux
SOS Enfants, qui se déroule près de 200 sos écoles dans le monde en développement, a organisé cette sélection. Cliquez ici pour plus d'informations sur les enfants SOS.
Exponentiation est une mathématique opération, écrit un n, de deux nombres, les base un et l'exposant n. Lorsque n est un positif entier , exponentiation correspond à répétée multiplication :
de même que la multiplication par un nombre entier correspondant à répétées outre :
L'exposant est généralement représenté comme un Exposant à droite de la base. Le exponentiation un n peut être lu comme: une élevé à la puissance n-ième ou élevé à la puissance [de] n, ou plus brièvement: a à la puissance n-ième ou à la puissance [de] n ou encore plus brièvement: un à la n. Certains exposants peuvent être lus d'une certaine manière; par exemple un deux est généralement lu comme un carré et un 3 comme un cube.
La puissance d'un n peut également être définie lors de l'exposant n est un entier négatif. Lorsque la base a est un nombre réel positif, exponentiation est défini pour les exposants réels et même complexes n. La spéciale fonction exponentielle e x est fondamental pour cette définition. Il permet les fonctions de la trigonométrie à se exprimer par exponentiation. Cependant, lorsque la base ne est pas un un nombre réel positif et l'exposant n est pas un entier, un n ne peut pas être défini comme un unique, d'une fonction continue.
Où l'exposant de l'exponentiation est une matrice est utilisée pour résoudre des systèmes équations différentielles linéaires.
Exponentiation est utilisé omniprésente dans de nombreux autres domaines ainsi, y compris l'économie, la biologie, la chimie, la physique et l'informatique, avec des applications telles que l'intérêt composé, la croissance de la population, chimiques cinétique de la réaction, vague comportement, et cryptographie à clé publique.
Exponentiation avec exposants entiers
L'opération d'exponentiation avec des exposants entiers ne nécessite algèbre élémentaire .
Exposants entiers positifs
2 = a · un est appelé carré d'un parce que la zone d'un carré de côté de longueur a est un deux.
3 = a · une · un est appelé cube, parce que le volume d'un cube avec une longueur latérale est 3.
Donc 3 2 est prononcé "trois carré», et deux 3 est "deux cubes".
L'exposant dit combien de copies de la base sont multipliés ensemble. Par exemple, 3 5 = 3 · 3 · 3 · 3 · 3 = 243. La base 3 apparaît cinq fois dans la multiplication répétée, puisque l'exposant est 5. Ici, 3 est la base, 5 est l'exposant, et 243 est la puissance ou, plus précisément, la cinquième puissance de 3 ou 3 élevé à la puissance cinq.
Le mot «en relief» est généralement omise, et le plus souvent «pouvoir» ainsi, donc 3 5 est généralement prononcé "trois à la cinquième" ou "trois à cinq".
Formellement, puissances ayant des exposants entiers positifs peuvent être définies par l'état initial a 1 = a et la une relation de récurrence n 1 = a · un n.
Exposants et une nulle
Notez que 3 1 est le produit d'un seul 3, ce qui est évidemment trois.
Notez également que 3 5 = 3 · 3 4. Aussi 3 4 = 3 · 3 3. La poursuite de cette tendance, nous devrions avoir
- 3 = 1 3 3 0 ·.
Une autre façon de faire est que lorsque n, m, et n - m est positif (et si x ne est pas égal à zéro), on peut voir en comptant le nombre d'occurrences de x que
Étendue au cas que n et m sont égaux, l'équation se lirait
depuis le numérateur et le dénominateur sont égaux. Par conséquent, nous prenons cela comme la définition de x 0.
Par conséquent, nous définissons 3 0 = 1, de sorte que l'égalité ci-dessus détient. Cela conduit à la règle suivante:
- Ne importe quel nombre à la puissance 1 est lui-même.
- Tout nombre différent de zéro à la puissance 0 est une; une interprétation de ces pouvoirs est aussi produits vides. Le cas de 0 0 est discutée ci-dessous .
Interprétation combinatoire
Pour les entiers non-négatifs N et M, la puissance n m est égale à la cardinal de l'ensemble des m - un n tuples de -Element ensemble, ou le nombre de mots m de -Lettre d'un n -lettre alphabet.
- 0 5 = | {} | = 0. Il n'y a pas 5-tuple de l'ensemble vide.
- 1 4 = | {(1,1,1,1)} | = 1. Il est un 4-uplet d'un ensemble à un élément.
- 2 3 = | {(1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1, 2), (2,2,1), (2,2,2)} | = 8. Il ya huit 3-uplets d'un ensemble de deux éléments.
- 3 2 = | {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3, 2), (3,3)} | = 9. Il ya 9 2-uplets d'un ensemble à trois éléments.
- 4 1 = | {(1), (2), (3), (4)} | = 4. Il existe une 4-uplets d'un ensemble à quatre éléments.
- 5 0 = | {()} | = 1. Il est exactement un vide tuple.
Voir aussi EXPONENTIATION sur des ensembles .
Exposants entiers négatifs
Élever un nombre différent de zéro à la puissance -1 produit son réciproque.
Ainsi:
Raising 0 à une puissance négative impliquerait division par 0, et ainsi ne est pas défini.
Un exposant entier négatif peut également être considérée comme répétée division par la base. Ainsi 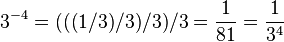 .
.
Identités et propriétés
Le plus important identité satisfaite par élévation à une puissance entière est:
Cette identité a pour conséquence:
pour a ≠ 0, et
 .
.
Un autre identité de base est
 .
.
Bien que l'addition et la multiplication sont commutatif (par exemple, 2 + 3 = 5 = 3 + 2 et 3 · 2 = 6 = 3 · 2), exponentiation est pas commutative: 2 3 = 8, mais 3 2 = 9.
De même, alors que l'addition et de multiplication sont associative (par exemple, (2 + 3) 4 2+ = 9 = (3 + 4) et (2 · 3) · 4 = 24 = 2 · (3 · 4), est exponentiation pas associatifs soit: 2 3 à la puissance 4 est 8 4 ou 4096, mais 2 à la puissance 3 4 2 est 81 ou 2.417.851.639.229.258.349.412.352 Sans parenthèses pour modifier l'ordre de calcul, la commande est généralement compris comme étant de droite à gauche.:
Pouvoirs de dix
- Voir Notation scientifique
Puissances de 10 sont facilement calculés dans la base dix ( décimal système) Numéro. Par exemple, 10 = 8 100 000 000.
Exponentiation avec la base 10 est utilisé dans la notation scientifique pour décrire les grandes ou de petites quantités. Par exemple, 299 792 458 (la vitesse de la lumière dans le vide, en mètres par seconde) peut être écrit comme 2,99792458 · 10 8 puis approchée que 2,998 · 10 8, (ou parfois 299,8 · 10 6 ou 299.8E + 6, en particulier dans le logiciel de l'ordinateur).
Préfixes SI basés sur des puissances de 10 sont également utilisés pour décrire petites ou grandes quantités. Par exemple, le préfixe kilo signifie 10 3 = 1000, donc un kilomètre est 1000 mètres.
Pouvoirs de deux
Le positif des puissances de 2 sont importants dans la science informatique , car il ya 2 n valeurs possibles pour un n - bit variable. Voir système de numération binaire .
Pouvoirs de deux sont importants dans la théorie des ensembles depuis un ensemble de n membres a une puissance définie, ou un ensemble de tous les sous-ensembles de l'ensemble original, avec 2 n membres.
Les puissances négatives de deux sont couramment utilisés, et les deux premiers ont des noms spéciaux: moitié, et trimestre.
Pouvoirs d'un
Les puissances entières de l'un sont une: 1 n = 1.
Pouvoirs de zéro
Si l'exposant est positif, la puissance du zéro est nul: 0 n = 0, où n> 0.
Si l'exposant est négatif, la puissance de zéro (0 - n, où n> 0) est toujours pas défini, car la division par zéro est implicite.
Si l'exposant est zéro, certains auteurs définissent 0 0 = 1, alors que d'autres laissent indéfini, comme on le verra ci-dessous .
Pouvoirs du moins un
Les pouvoirs du moins un sont utiles pour exprimer des séquences alternées.
Si l'exposant est pair, la puissance moins un est une: (-1) 2 n = 1.
Si l'exposant est impair, la puissance moins un est moins un: (-1) 2 n 1 = -1.
Pouvoirs de l'unité imaginaire
Les pouvoirs de l' unité imaginaire i sont utiles pour exprimer des séquences de période 4. Voir, par exemple Racine de l'unité # Périodicité.
Pouvoirs du e
Le numéro e, la base du logarithme naturel , est un bien étudié constante approximativement égale à 2,718. Elle peut être approximée par de grandes puissances positives ou négatives de nombres à proximité de l'un, tels que
ou
et définie comme étant la limite
Tout pouvoir entier non nul de e peut être calculée comme ceci:
La fonction exponentielle , défini par
a des applications dans de nombreux domaines des mathématiques et de la science. Cette définition de l'e x correspond à la définition du e k lorsque x est un entier, mais elle se applique aussi pour les valeurs fractionnaires, réels ou complexes de x, et même lorsque x est une matrice carrée , qui est utilisé dans les équations différentielles ordinaires .
Une autre formule populaire est la série de puissance
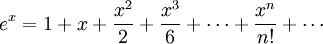 .
.
Pouvoirs de nombres réels
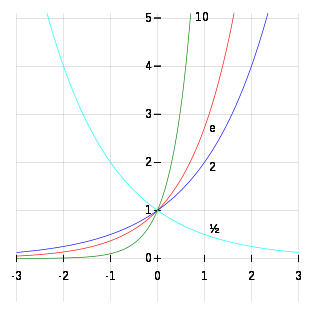

Élever un nombre réel positif à un pouvoir qui ne est pas un nombre entier peut être réalisé de deux façons.
- Nombre rationnel exposants peuvent être définies en termes de n ième racines, et des exposants non nuls arbitraires peuvent ensuite être définies par la continuité.
- Le logarithme naturel peut être utilisé pour définir des exposants réels à l'aide de la fonction exponentielle.
Les identités et les propriétés indiquées ci-dessus sont vraies pour les exposants non entiers ainsi.
Principal n-ième racine
Un n-ième racine d'un certain nombre a est un nombre b tel que b n = a.
Lorsqu'on se réfère à la n ième racine d'un nombre réel a, on suppose que ce qui est souhaité est la principale racine n ième du nombre. Si a est un nombre réel, et n est un nombre entier positif, alors la solution vraie unique avec le même signe en tant que l'équation
est appelée le principal n ième racine d'un, et est notée ![\ Sqrt [n] {a}](../../images/114/11497.png) en utilisant le radical symbole
en utilisant le radical symbole  .
.
![x = a ^ {\ frac {1} {n}} = \ sqrt [n] {a}](../../images/114/11499.png) .
.
Par exemple: 4 1/2 = 2, 8 1/3 = 2, (-8) 1/3 = -2,.
Notez que si n est égal à même, les nombres négatifs ne auront pas un principal n ième racine.
Puissances rationnelles de nombres réels positifs
Exponentiation avec une rationnelle exposant m / n peut être définie comme
![un ^ {\ frac {m} {n}} = \ left (un ^ m \ right) ^ {\ frac {1} {n}} = \ sqrt [n] {a} ^ m](../../images/115/11500.png) .
.
Par exemple, 8 2/3 = 4.
Puisque tout nombre réel peut être approchée par des nombres rationnels, à une exponentiation réel exposant k arbitraire peut être défini par continuité avec la règle
où la limite est prise seulement sur des valeurs rationnelles de r.
Par exemple, si
puis
De réels pouvoirs de nombres réels positifs
Le logarithme naturel ln (x) est l' inverse de la fonction exponentielle e x. Il est défini pour chaque nombre réel positif b et satisfait l'équation
En supposant b x est déjà défini, exponentielles et les logarithmes règles donnent l'égalité
Cette égalité peut être utilisé pour définir exponentiation avec toute base réelle b positif
Cette définition du nombre réel pouvoir b x est d'accord avec la définition donnée ci-dessus en utilisant des exposants rationnels et la continuité. La définition de l'élévation à une puissance à l'aide des logarithmes est plus commun dans le cadre de nombres complexes, comme discuté ci-dessous.
Certaines puissances rationnelles de nombres réels négatifs
Ni la méthode du logarithme, ni la méthode d'exposant fractionnaire peuvent être utilisés pour définir un k comme un nombre réel d'un négatif et un nombre réel arbitraire nombre réel k. Dans certains cas particuliers, une définition est possible: des puissances entières de nombres réels négatifs sont des nombres réels, et les pouvoirs rationnels de la forme d'un m / n où n est impair peut être calculé en utilisant les racines. Mais comme il n'y a pas de nombre réel x tel que x 2 = -1, la définition d'un m / n quand n est pair et m est impair doivent utiliser le unité imaginaire i, comme décrit plus en détail dans la section suivante.
La méthode de logarithme ne peut pas être utilisé pour définir un k comme un nombre réel quand un <0 car e x est positive pour chaque nombre réel x, alors connectez-vous (a) ne peut pas être un nombre réel.
La méthode d'exposant rationnelle ne peut pas être utilisé pour les valeurs négatives d'un car elle repose sur la continuité. La fonction f (r) = a r a une extension continue unique à partir des nombres rationnels aux nombres réels pour chaque a> 0. Mais quand un <0, la fonction f ne est même pas en continu sur l'ensemble des nombres rationnels r pour lesquels elle est définie.
Par exemple, prenez = -1. La n ième racine de -1 est -1 pour chaque nombre impair naturel n. Donc, si n est un entier positif impair, (-1) (m / n) = -1 si m est impair, et (-1) (m / n) = 1 si m est pair. Ainsi, l'ensemble des nombres rationnels q pour lesquels -1 q = 1 est dense dans les nombres rationnels, comme ce est l'ensemble de q pour lequel q = -1 -1. Cela signifie que la fonction q (-1) ne est pas continue à ne importe quel nombre rationnel q où elle est définie.
Pouvoirs imaginaires de e
L' interprétation géométrique des opérations sur les nombres complexes et la définition des pouvoirs de e est la clé pour comprendre i e · x pour x réel. Considérons le triangle (0, 1, 1+ i · x / n). Pour les grandes valeurs de n le triangle est presque un secteur circulaire avec un petit angle au centre égal à x / n radians. Les triangles (0, (1+ i · x / n) k, (1+ i · x / n) k 1) sont mutuellement similaire pour toutes les valeurs de k. Donc, pour les grandes valeurs de N le point de (1+ ix / n) limitant n est le point sur le cercle unité dont l'angle de l'axe réel positif x est radians . Les coordonnées polaires de ce point sont (r, θ) = (1, x), et les coordonnées cartésiennes sont (cos (x), sin (x)). Alors E i · x = cos (x) + i · sin (x), et ce est La formule d'Euler, reliant l'algèbre de trigonométrie au moyen de nombres complexes .
Les solutions de l'équation z = e 1 sont des multiples entiers de π · 2 · i:
Plus généralement, si e b = a, alors chaque solution e z = A peut être obtenue en ajoutant un multiple entier de 2 · π · i to B:
 .
.
Ainsi, la fonction exponentielle complexe est un fonction périodique de période 2 · π · i.
Les fonctions trigonométriques
Il résulte de La formule d'Euler que la fonctions trigonométriques cosinus et sinus sont
Historiquement, les sinus et cosinus sont définis géométriquement avant l'invention de nombres complexes. La formule ci-dessus réduit les formules complexes pour fonctions trigonométriques d'une somme dans la formule d'exponentiation simples
Utilisation exponentiation avec des exposants complexes on n'a pas besoin d'étudier la trigonométrie.
Pouvoirs complexes de e
La puissance e x + i · y est calculé e x · e · i y. Le facteur réel e x est la valeur absolue de l'e x + i · Y et le facteur complexe e i · y mentionne le direction de e x + i · y.
Pouvoirs complexes de nombres réels positifs
Si a est un nombre réel positif, et z est un nombre complexe, le pouvoir a z est défini comme e z · ln (a), où x = ln (a) est la vraie solution unique de l'équation x = e a. Donc, de la même méthode de travail pour les exposants réels fonctionne également pour les exposants complexes. Par exemple:
- 2 i = e i · ln (2) = cos (ln (2)) + i · sin (ln (2)) = i · 0,63896 0.7692+
- e i = i · 0.54030+ 0,84147
- 10 i = i · -0.66820+ 0,74398
- (E 2 · π) = 535,49 i i = 1
Pouvoirs de nombres complexes
Des puissances entières de nombres complexes sont définis par multiplication ou division répétée comme ci-dessus. Pouvoirs complexes de réels positifs sont définis via e x comme ci-dessus. Ce sont des fonctions continues. Essayer d'étendre ces fonctions au cas général des puissances non entières de nombres complexes qui ne sont pas réels positifs conduit à des difficultés. Soit nous définissons fonctions discontinues ou fonctions multiples. Aucune de ces options sont entièrement satisfaisante.
La puissance rationnelle d'un nombre complexe doit être la solution à une équation algébrique. Par exemple, w = z 1/2 doit être une solution de l'équation z = w 2. Mais si w est une solution, il en est - w, parce que (-1) 2 = 1. Donc, l'équation algébrique w = z 2 ne est pas suffisante pour définir z 2.1. Choisir l'une des deux solutions que la principale valeur de z moitié nous laisse avec une fonction qui ne est pas continue, et les règles habituelles pour la manipulation des pouvoirs nous égarer.
Le logarithme d'un nombre complexe
Une solution, z = log a, à l'équation e z = a, est appelé le valeur principale du logarithme complexe. Il est l'unique solution dont la partie imaginaire réside dans le . intervalle (-π, π] Par exemple, log 1 = 0, log (-1) = π i, i = connecter π i / 2, et log (-. i) = i -π / 2 La valeur principale de le logarithme est connue comme une branche du logarithme; autres branches peuvent être spécifiées en choisissant une gamme différente pour la partie imaginaire du logarithme La frontière entre les branches est connu comme un. Branch Cut. La valeur principale a une coupure de branche se étendant depuis l'origine le long de l'axe réel négatif, et est discontinue à chaque point de la branche coupée.
Alimentation complexe d'un nombre complexe
Le grand complexe de puissance a b d'un nombre complexe non nul est défini comme un
Lorsque l'exposant est un nombre rationnel de la puissance z = a n / m est une solution de l'équation z = m a n.
Le calcul des pouvoirs complexes est facilitée par une conversion de la base en forme polaire, comme décrit en détail ci-dessous .
Racines complexes de l'unité
Un nombre complexe a tel que a = 1 pour n un nombre entier positif n est un n-ième racine de l'unité. Géométriquement, la n-ième racines de l'unité se trouvent sur le cercle unité du plan complexe aux sommets d'un n-gon régulier avec un sommet sur le nombre réel 1.
Si z n = 1, mais z k ≠ 1 pour tous les nombres naturels k tel que 0 <k <n, alors z est appelé un n ième primitive racine de l'unité. L'unité négative -1 est la seule racine carrée primitive de l'unité. L' unité imaginaire i est l'une des deux racines primitives 4-ème de l'unité; l'autre est - i.
Le nombre e 2 πi (1 / n) est le n ième primitive racine de l'unité avec le plus petit positif argumentation complexe. (Il est parfois appelé le principal n ième racine de l'unité, même si cette terminologie ne est pas universelle et ne doit pas être confondu avec le principale valeur de n √ 1, qui est 1.)
Les autres n ième racines de l'unité sont donnés par
pour 2 ≤ k ≤ n.
Racines de nombres complexes arbitraires
Bien qu'il existe une infinité de valeurs possibles pour un logarithme complexe général, il ne existe qu'un nombre fini de valeurs de la puissance de z dans le cas particulier important lorsque z = 1 / n et n est un nombre entier positif. Il se agit de la n ième racines d'un; ce sont des solutions de l'équation x = n a. Comme avec de vraies racines, une deuxième root est aussi appelé une racine carrée et un troisième root est aussi appelé une racine cubique.
Il est classique en mathématiques pour définir un 1 / n comme la principale valeur de la racine. Si a est un nombre réel positif, il est également classique pour sélectionner un nombre réel positif que la valeur principale de la racine d'un 1 / n. Pour les nombres complexes généraux, le n ième racine avec le plus petit argument est souvent choisie comme la principale valeur de la n ième opération de racine, comme avec les valeurs principales de racines de l'unité.
L'ensemble des n ième racines d'un nombre complexe a est obtenu en multipliant la valeur nominale de 1 / n par chacun des n ième racines de l'unité. Par exemple, les racines quatrièmes de 16 sont 2, -2, 2 i, i et -2, parce que la valeur principale de la racine quatrième de 16 est 2 et le quatrième racines de l'unité sont 1, -1, i, et - i.
Informatique pouvoirs complexes
Il est souvent plus facile à calculer pouvoirs complexes en écrivant le numéro à exponentielle en forme polaire . Chaque nombre complexe z peut être écrit sous la forme polaire
où r est un nombre réel non négatif et θ est le (réel) l'argument de z. L'argument, comme le logarithme complexe, possède de nombreuses valeurs possibles pour chaque z et donc un Branch Cut permet de choisir une valeur spécifique. La forme polaire a une interprétation géométrique simple: si un nombre complexe u + iv est considéré comme représentant un point (u, v) dans le plan complexe en utilisant les coordonnées cartésiennes , alors (r, θ) est le même point de coordonnées polaires . Ce est, r est le "rayon" r 2 = u 2 + v 2 et θ est le "angle" θ = atan2 (v, u). La coupure de branche correspond à l'idée que un angle θ polaire est ambiguë, car tout multiple de 2π pourrait être ajouté à θ sans changer l'emplacement du point. La valeur principale (coupure de branche la plus courante), comme mentionné ci-dessus, correspond à θ choisie dans l'intervalle (-π, π].
Afin de calculer la puissance d'un complexe b, écrire un sous forme polaire:
 .
.
Puis
et ainsi
Si b est décomposée comme c + di, alors la formule pour une b peut se écrire plus explicitement que
Cette formule finale permet pouvoirs complexes pour être calculées facilement de décompositions de la base en forme polaire et l'exposant en forme cartésienne. Il est montré ici à la fois sous forme polaire et sous forme cartésienne (via l'identité d'Euler).
Les exemples suivants utilisent la valeur du capital, la coupe de branche qui provoque θ être dans l'intervalle (-π, π] Pour calculer i i, i écrire dans des formes polaires et cartésiennes.:
Ensuite, la formule ci-dessus, avec r = 1, θ = π / 2, c = 0 et d = 1, on obtient:
De même, à trouver (-2) 3 + 4 i, calculer la forme polaire de -2,
et utiliser la formule ci-dessus pour calculer
La valeur d'une puissance complexe dépend de la branche utilisé. Par exemple, si la forme polaire i = 1 e i (5π / 2) est utilisée pour calculer i i, la puissance se avère e -5π / 2; la principale valeur de i i, calculé ci-dessus, est e -π / 2.
Défaillance de l'alimentation et de logarithme identités
Identités de pouvoirs et logarithmes qui détiennent pour les nombres réels positifs peuvent échouer lorsque les nombres réels positifs sont remplacés par des nombres complexes arbitraires. Il n'y a aucune méthode pour définir les pouvoirs complexes ou le logarithme complexe que les fonctions de valeurs complexes tout en préservant les identités possèdent ces opérations dans les nombres réels positifs.
Un exemple impliquant logarithmes concerne le journal de la règle (un b) = b · log A, qui détient chaque fois qu'un est un nombre réel positif et b est un nombre réel. Le calcul suivant montre que cette identité ne tient pas en général pour la valeur principale du logarithme complexe quand un ne est pas un nombre réel positif:
Quelle que soit la branche du logarithme est utilisé, une défaillance similaire de l'identité existera toujours.
Un exemple impliquant règles d'alimentation concerne les identités
Ces identités sont valides lorsque a et b sont des nombres réels positifs et c est un nombre réel. Mais un calcul utilisant des valeurs principales montre que
et
Ces exemples montrent que les pouvoirs et les logarithmes complexes ne se comportent pas de la même manière que leurs homologues réels, et donc la prudence est nécessaire lorsque l'on travaille avec les versions de ces opérations complexes.
Zéro à la puissance zéro
L'évaluation de 0 0 pose un problème, parce que le raisonnement mathématique différente conduit à des résultats différents. Le meilleur choix pour la valeur dépend du contexte. Selon Benson (1999), "Le choix se il faut définir 0 0 est basé sur la commodité, pas correcte." Il ya deux principaux traitements dans la pratique, un de mathématiques discrètes et l'autre de l'analyse.
Dans de nombreux contextes, en particulier dans les fondations et combinatoire, 0 0 est définie à 1. Cette définition se pose dans les traitements fondamentaux des nombres naturels comme cardinaux finis , et est utile pour raccourcir identités combinatoires et la suppression des cas particuliers de théorèmes, comme illustré ci-dessous. Dans de nombreux autres paramètres, 0 0 ne est pas définie. Dans le calcul , 0 0 est un forme indéterminée, qui doit être analysé plutôt que évaluée. En général, l'analyse mathématique traite comme 0 0 undefined afin que la fonction exponentielle être continue.
Justifications pour définir 0 0 = 1 comprennent:
- Lorsque 0 0 est considéré comme un vide produit de zéros, sa valeur est 1.
- L' interprétation combinatoire de 0 0 est le nombre de lignes vides d'éléments de l'ensemble vide. Il ya exactement un vide tuple.
- De manière équivalente, l' interprétation de la théorie des ensembles de 0 0 est le nombre de fonctions de l'ensemble vide à l'ensemble vide. Il est exactement une telle fonction, le fonction vide.
- Il simplifie grandement la théorie de polynômes et séries de puissance qu'un terme constant peut être écrit pour une hache 0 x arbitraire. Par exemple:
- La formule pour les coefficients dans un produit de polynômes perdrait beaucoup de sa simplicité si les termes constants devaient être traités spécialement.
- Une série de puissance tel que
 ne est pas valable pour x = 0 0 0 moins, qui apparaît dans le numérateur du premier terme de la série, est 1. Sinon il faudrait utiliser l'identité plus
ne est pas valable pour x = 0 0 0 moins, qui apparaît dans le numérateur du premier terme de la série, est 1. Sinon il faudrait utiliser l'identité plus  .
. - Le théorème de binôme
 ne est pas valable pour x = 0, à moins 0 0 = 1. En définissant 0 0 à 1, un cas particulier du théorème peut être éliminé.
ne est pas valable pour x = 0, à moins 0 0 = 1. En définissant 0 0 à 1, un cas particulier du théorème peut être éliminé.
- En le calcul différentiel, le règle de puissance
 ne est pas valide pour n = 1 à x = 0 0 0 = moins 1. Définir cette façon élimine la nécessité d'un cas particulier de la règle de puissance.
ne est pas valide pour n = 1 à x = 0 0 0 = moins 1. Définir cette façon élimine la nécessité d'un cas particulier de la règle de puissance.
Dans les contextes où l'exposant peut varier en continu, il est généralement préférable de traiter 0 0 comme quantité mal défini. Justifications pour traiter comme undefined comprennent:
- La valeur 0 0 se pose souvent la limite officielle de fonctions exponentielles, f (x) g (x), où f (x) et g (x) approche 0 quand x tend vers un (une constante ou l'infini). Là, 0 0 suggère [lim f (x)] lim g (x), qui est une quantité bien définie et est la valeur correcte de lim f (x) g (x) lorsque des constantes non nulles f et d'approche g, mais ne est pas bien défini quand approche f et g 0. Le même raisonnement se applique à certains pouvoirs impliquant l'infini ,
 et
et  . Une manière plus abstraite de dire ce est la suivante: La fonction réelle x y des deux non négatifs variables réelles x et y ne est pas continue au point (x, y) = (0, 0), et ainsi de 0 à 0 ne est pas déterminée par la continuité. Autrement dit, la fonction x y n'a pas d'extension continue à partir du premier quadrant ouvert pour inclure le point (0,0). La règle de calcul, que
. Une manière plus abstraite de dire ce est la suivante: La fonction réelle x y des deux non négatifs variables réelles x et y ne est pas continue au point (x, y) = (0, 0), et ainsi de 0 à 0 ne est pas déterminée par la continuité. Autrement dit, la fonction x y n'a pas d'extension continue à partir du premier quadrant ouvert pour inclure le point (0,0). La règle de calcul, que  si les deux côtés de l'équation sont définis, échouerait si 0 0 ont été définis.
si les deux côtés de l'équation sont définis, échouerait si 0 0 ont été définis. - La fonction z z, considérée comme une fonction d'un nombre complexe z variable et défini comme e z journal z est undefined à z = 0 car journal z ne est pas défini à z = 0. De plus, parce z z a une logarithmique point z = 0 de la branche, il ne est pas commun à étendre le domaine de z z à l'origine dans ce contexte.
Traitement des langages de programmation
Les langages de programmation informatique qui évaluent 0 0 à 1 comprennent J, Java , Python , Ruby, Haskell, ML, Scheme, MATLAB, et la calculatrice de Microsoft Windows.
Maple simplifie de 0 à 1 et un 0 à 0, même si aucune contrainte sont placées sur un, et évalue 0 0-1.
Recherche Google lorsqu'il est utilisé pour sa fonction calculatrice évalue 0 0-1.
Mathematica simplifie un 0-1, même si aucune contraintes sont placées sur un. Il ne simplifie pas un 0, et il prend 0 0 d'être une forme indéterminée.
Dans le .NET Framework, le méthode System.Math.Pow traite 0 0 à 1.
Pouvoirs avec l'infini
Expressions exponentielles impliquant l'infini peuvent être considérés comme des généralisations de types plus familiers de exponentiation, mais il ya au moins deux types distincts de généralisation fortement au cas infini. D'une part, il ya la combinatoire interprétation théorique ou ensemble; voir exponentiation des nombres cardinaux .
D'autre part, on peut trouver des expressions telles que  et
et  provenant d'analyse pour la même raison que 0 0, et ils ne sont pas définis pour la même raison. Ce est, il est vrai que (lim f (x)) lim g (x) = lim f (x) g (x) lorsque constantes non nulle fini F et d'approche de g, mais pas quand ils se approchent 0 ou l'infini; puis, à la limite de la puissance peut être ne importe quoi, pas prévisibles à partir des limites de f et g.
provenant d'analyse pour la même raison que 0 0, et ils ne sont pas définis pour la même raison. Ce est, il est vrai que (lim f (x)) lim g (x) = lim f (x) g (x) lorsque constantes non nulle fini F et d'approche de g, mais pas quand ils se approchent 0 ou l'infini; puis, à la limite de la puissance peut être ne importe quoi, pas prévisibles à partir des limites de f et g.
Il est logique de dire que  Si ce est simplement interprétée comme une abréviation pour le théorème que si f et g approche à la fois l'infini quand x tend vers a, alors lim f (x) g (x) est aussi infinie. (De même,
Si ce est simplement interprétée comme une abréviation pour le théorème que si f et g approche à la fois l'infini quand x tend vers a, alors lim f (x) g (x) est aussi infinie. (De même,  ,
,  , Etc.)
, Etc.)
Calculer efficacement une puissance
La méthode la plus simple de calculer a n n-1 nécessite des opérations de multiplication, mais elle peut être calculée de façon plus efficace comme illustré par l'exemple suivant. Pour calculer 2 100, notez que 100 = 96 + 4 et 96 = 3 * 32. Calculer la suivante dans l'ordre:
- 2 2 = 4
- (2 2) 2 = 2 4 = 16
- (2 4) 2 = 2 8 = 256
- (2 8) 2 = 2 16 = 65536
- (2 16) 2 = 2 32 = 4294967296
- 2 32 2 32 2 32 2 4 = 2 100
Cette série d'étapes ne nécessite huit opérations de multiplication au lieu de 99.
En général, le nombre d'opérations de multiplication nécessaires pour calculer un n peut être réduite à Θ (log n) en utilisant Exponentiation rapide ou (plus généralement) exponentiation outre-chaîne. Trouver la séquence minimale de multiplications (dans la chaîne d'addition longueur minimale de l'exposant) pour un n est un problème difficile pour lequel aucun des algorithmes efficaces sont actuellement connus, mais de nombreux algorithmes heuristiques raisonnablement efficaces sont disponibles.
La notation exponentielle pour les noms de fonction
Déposer une exposant entier après le nom ou le symbole d'une fonction, comme si la fonction étaient élevés à une puissance, se réfère communément à répéter la composition de fonctions plutôt que la multiplication répétée. Ainsi f 3 (x) peut signifier f (f (f (x))); en particulier, f -1 (x) désigne généralement la fonction inverse de f.
Cependant, pour des raisons historiques, une syntaxe spéciale se applique aux fonctions trigonométriques : un exposant positive appliquée à l'abréviation de la fonction signifie que le résultat est élevé à ce pouvoir, tout en un exposant de -1 désigne la fonction inverse. Ce est, sin 2 x est juste un raccourci pour écrire (sin x) 2 sans l'aide de parenthèses, alors que sin -1 x se réfère à la fonction inverse de la sinus, également appelé arcsin x. Il ne est pas nécessaire pour un raccourci pour les inverses des fonctions trigonométriques puisque chacun a son propre nom et abréviation, par exemple 1 / sin (x) = (sin x) -1 est csc x. Une convention similaire se applique aux logarithmes, où log 2 (x) = (log (x)) 2 et il n'y a pas d'abréviation courante pour log (log (x)).
Généralisations de exponentiation
Exponentiation en algèbre abstraite
Exponentiation pour exposants entiers peut être définie pour les structures très généraux dansl'algèbre abstraite.
Soit X soit un ensemble avec une puissance associative opération binaire, que nous écrirons multiplicativement. Dans cette situation très générale, on peut définir x n pour tout élément x de X et tout non nulle nombre naturel n , simplement en multipliant x par lui-même n fois; par définition, le pouvoir associativité signifie qu'il n'a pas d'importance dans quel ordre nous effectuons les multiplications.
Supposons maintenant en outre l'opération qui a un élément ayant une identité 1. Puis on peut définir x 0 soit égal à 1 pour chaque x . Maintenant x n est défini pour tout entier naturel n , y compris 0.
Enfin, supposons que l'opération a inverses, et que la multiplication est associative (de sorte que le magma est un groupe ). Ensuite, nous pouvons définir x -n à l'inverse de x n où n est un nombre naturel. Maintenant x n est défini pour tout entier n et tout x dans le groupe.
Exponentiation dans ce sens purement algébrique satisfait aux lois suivantes (à chaque fois que les deux parties sont définies):
Ici, nous utilisons une division slash ("/") pour indiquer multipliant par l'inverse, afin de réserver le symbole x -1 pour élever x à la puissance -1, plutôt que l'inverse de x . Cependant, comme l'un des états ci-dessus lois, x -1 est toujours égal à l'inverse de x , de sorte que la notation n'a pas d'importance à la fin.
Si en plus l'opération de multiplication estcommutative(de sorte que l'ensembleXest ungroupe abélien), puis nous avons quelques lois supplémentaires:
- (xy)n=xnyn
- (x/y)n=xn/yn
Si nous prenons toute cette théorie de l'exponentiation dans un contexte algébrique mais écrivons l'opération binaire additive, "la multiplication exponentielle est répété", puis peut être réinterprété comme " la multiplication est répété plus ". Ainsi, chacune des lois de exponentiation ci-dessus a un analogue entre les lois de la multiplication.
Quand on a plusieurs opérations autour, celles-ci pouvant être répété en utilisant exponentiation, il est courant d'identifier les opérations qui se répète en plaçant son symbole dans l'exposant. Ainsi, x *n est x * ··· * x , alors x #n est x ··· # # x , quelles que soient les opérations * et # soient.
Exposant notation est également utilisé, en particulier dans la théorie des groupes , pour indiquer la conjugaison. Autrement dit, g h = h -1 gh , où g et h sont des éléments d'un certain groupe . Bien que la conjugaison obéit à certains des mêmes lois que exponentiation, il est pas un exemple de la multiplication répétée dans tous les sens. Un quandle est une structure algébrique dans laquelle ces lois de conjugaison jouent un rôle central.
Exponentiation sur des ensembles
Si n est un nombre naturel et A est un ensemble arbitraire, l'expression A n est souvent utilisé pour désigner l'ensemble des ordonnées n -uplets d'éléments de A . Cela équivaut à laisser un n désignent l'ensemble des fonctions de l'ensemble {0, 1, 2, ..., n } -1 à l'ensemble A ; le n Z-uplets ( un 0 , un 1 , un 2 , ..., a n-1 ) représente la fonction qui envoie i à un je .
Pour un infini nombre cardinal κ et un ensemble A , la notation A κ est également utilisé pour désigner l'ensemble des fonctions d'un ensemble de κ de taille à un . Cela est parfois écrit κ A pour le distinguer du cardinal exponentiation, défini ci-dessous.
Cette exponentielle généralisée peut également être défini pour les opérations sur les ensembles ou pour des ensembles avec supplémentaire structure. Par exemple, dans l'algèbre linéaire , il est logique d'index sommes directes de espaces vectoriels sur des ensembles d'index arbitraires. Autrement dit, nous pouvons parler de
où chaque V je est un espace vectoriel. Ensuite, si V je = V pour chaque i , la somme directe résultant peut être écrit en notation exponentielle comme V (+)N , ou tout simplement V N avec la compréhension que la somme directe est la valeur par défaut. Nous pouvons à nouveau remplacer la série N avec un nombre cardinal n d'obtenir V n , bien que sans choix d'une norme spécifique défini de cardinal n , ceci est défini uniquement à isomorphisme. Prenant V soit le domaine R des nombres réels (pensée comme un espace vectoriel sur lui-même) et n y avoir un certain nombre naturel , nous obtenons l'espace vectoriel qui est le plus couramment étudié en algèbre linéaire, l' espace euclidien R n .
Si la base de l'opération d'exponentiation est un ensemble, l'opération d'exponentiation est le produit cartésien, sauf indication contraire. Depuis plusieurs produits cartésiens produisent un n - uplet, qui peut être représenté par une fonction sur un ensemble de cardinal échéant, S N devient tout simplement l'ensemble des fonctions de N à S dans ce cas:
Cela correspond à l'exponentiation des nombres cardinaux, dans le sens où | S N | = | S | |N| , où | X | est le cardinal de X . Lorsque N = 2 = {0,1}, nous avons | 2 X | = 2 |X| , où 2 X , généralement désigné par P X , est le jeu de puissance de X ; chaque sous-ensemble Y de X correspond à une fonction unique sur X prenant la valeur 1 pour x ∈ Y et 0 pour x ∉ Y .
Exponentiation dans la théorie des catégories
Dans un Cartésienne catégorie fermée, l' opération exponentielle peut être utilisé pour soulever un objet arbitraire à la puissance d'un autre objet. Ceci généralise le produit cartésien dans la catégorie des ensembles.
Exponentiation des nombres cardinaux et ordinaux
Enthéorie des ensembles, il ya des opérations exponentielles pourcardinaletordinalnuméros.
Si κ et λ sont des nombres cardinaux, le κ d'expression λ représente le cardinal de l'ensemble des fonctions de tout ensemble de cardinal λ à un ensemble de cardinal κ. Si κ et λ sont finies alors ce d'accord avec l'opération exponentielle ordinaire. Par exemple, l'ensemble des 3-uplets d'éléments d'un ensemble 2-élément est de cardinal 8.
Exponentiation de nombres cardinaux est distinct de l'exponentiation de nombres ordinaux , qui est définie par une limite procédé. Dans les nombres ordinaux, exponentiation est définie par induction transfinie. Pour ordinaux α et β, l'α exponentielle β est la borne supérieure du produit ordinale a γ a sur tout γ <β.
Exponentiation répétée
Tout comme exponentiation des nombres naturels est motivée par multiplication répétée, il est possible de définir une opération sur la base de l'exponentiation répété; cette opération est parfois appelé tétration. Itération tétration conduit à une autre opération, et ainsi de suite. Cette séquence d'opérations est capturé par la fonction d'Ackermann.
Exponentiation en langages de programmation
La notation exposant x y est pratique dans l'écriture, mais gênant pour machines à écrire et des terminaux informatiques qui alignent les lignes de base de tous les caractères sur chaque ligne. De nombreux langages de programmation ont des façons différentes d'exprimer exponentiation qui ne pas utiliser les exposants:
- ↑ x y:Algol,Commodore BASIC
- x ^ y:BASIC, J, Matlab, R, Microsoft Excel,TeX(et ses dérivés),Haskell (pour les exposants entiers), et la plupart dessystèmes d'algèbre informatique
- x ** y: Ada, Bash, Fortran, FoxPro,Perl,Python, Ruby, SAS,ABAP, Haskell (pour virgule flottante exposants),Turing
- x * y: APL
- Puissance (x, y): Microsoft Excel, Delphi / Pascal (déclarée dans «Math» -unit)
- pow (x, y):C,C ++, PHP
- Math.pow (x, y):Java, JavaScript Modula-3
- Math.pow (x, y): C #
- (Exp xy):Common Lisp,Scheme
Dans Bash, C, C ++, C #, Java, JavaScript, PHP et Python, le symbole ^ représente bit XOR. En Pascal, il représente indirection.
Histoire de la notation
Le terme de puissance a été utilisé par Euclide pour le carré d'une ligne. Nicolas Chuquet utilisé une forme de notation exponentielle dans le 15ème siècle, qui a ensuite été utilisé par Henricus Grammateus et Michael Stifel. Samuel Jeake introduit le terme indices en 1696. Au 16ème siècle, Robert Recorde utilisé les termes carré, cube, zenzizenzic (quatrième pouvoir), surfolide (cinquième), zenzicube (sixième), deuxième surfolide (septième) et Zenzizenzizenzic (huitième).
Un autre synonyme historique,involution, est maintenant rare et ne doit pas être confondu avecson sens plus commun.


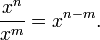




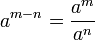





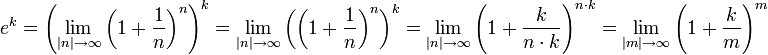


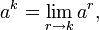

![5 ^ k \ environ 5 ^ {1,732} = 5 ^ {} 433/250 = \ sqrt [250] {5} ^ {433} \ environ 16,241.](../../images/115/11503.png)




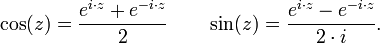

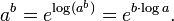



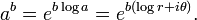
![\ Left (r ^ CE ^ {- d \ theta} \ right) e ^ {i (d \ log r + c \ theta)} = \ left (r ^ CE ^ {- d \ theta} \ right) \ gauche [\ cos (d \ log r + c \ theta) + i \ sin (d \ log r + c \ theta) \ right].](../../images/115/11517.png)