Mécanique des fluides
À propos de ce écoles sélection Wikipedia
SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . Parrainer un enfant de faire une réelle différence.
| Mécanique des milieux continus |
|---|
 |
Lois
|
Mécanique des solides
|
Mécanique des fluides
|
Rhéologie
|
Mécanique des fluides est l'étude de la façon dont fluides se déplacent et les forces sur eux. (Liquides comprennent des liquides et gaz .) Mécanique des fluides peuvent être divisés en statique des fluides, l'étude des fluides au repos, et la dynamique des fluides, l'étude des fluides en mouvement. Ce est une branche de mécanique des milieux continus, un sujet qui comptent modèles sans utiliser les renseignements qu'il est fait d'atomes. L'étude de la mécanique des fluides remonte au moins à l'époque de la Grèce antique, quand Archimède a fait un début sur la statique des fluides. Cependant, la mécanique des fluides, en particulier la dynamique des fluides, est un domaine de recherche actif avec de nombreux problèmes non résolus ou partiellement résolus. Mécanique des fluides peuvent être mathématiquement complexe. Parfois, il peut être mieux résolu par les méthodes numériques, typiquement en utilisant des ordinateurs. Une discipline moderne, appelé Computational Fluid Dynamics (CFD), est consacré à cette approche pour résoudre les problèmes de mécanique des fluides. Profitant également de la nature hautement visuelle de l'écoulement du fluide est Particle Image Velocimetry, une méthode expérimentale pour la visualisation et l'analyse de l'écoulement du fluide.
Relation à la mécanique des milieux continus
Mécanique des fluides est une sous-discipline de mécanique des milieux continus, comme illustré dans le tableau suivant.
| Continuum mécaniciens l'étude de la physique des matériaux en continu | Mécanique des solides: l'étude de la physique des matériaux continus avec une forme de repos définie. | Elasticité: qui décrit les matériaux qui retournent à leur forme au repos après une appliquée stress. | |
| Plasticité: qui décrit les matériaux qui se déforment de façon permanente après un grand effort appliqué assez. | Rhéologie: l'étude des matériaux avec les deux caractéristiques solides et des fluides | ||
| Mécanique des fluides: l'étude de la physique des matériaux continues qui prennent la forme de leur contenant. | Des fluides non newtoniens | ||
| Fluides newtoniens | |||
En vue mécanique, un fluide est une substance qui ne prend pas contrainte tangentielle; ce est pourquoi un fluide dans le repos a la forme de leur contenant un fluide vessel.And dans le repos ont nulle contrainte de cisaillement
Hypothèses
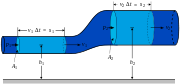
Comme tout modèle mathématique du monde réel, mécanique des fluides rend certaines hypothèses de base sur les matériaux étudiés. Ces hypothèses sont transformées en équations qui doivent être satisfaits si les hypothèses sont à vrai. Par exemple, considérons un fluide incompressible en trois dimensions. L'hypothèse que la masse est conservée signifie que pour ne importe quelle surface fermée fixe (comme une sphère) le taux d'adoption de masse de l'extérieur vers l'intérieur de la surface doit être le même que le taux de masse passant dans l'autre sens. (Sinon, la masse reste à l'intérieur constant, tout comme la masse extérieur). Cela peut être transformé en un équation intégrale sur la surface.
Mécanique des fluides suppose que chaque fluide obéit à la suivante:
- Conservation de la masse
- Conservation du moment
- L'hypothèse de continuum, détaillé ci-dessous.
En outre, il est souvent utile (et réaliste) d'assumer un fluide est incompressible - ce est la masse volumique du fluide ne change pas. Liquides peut souvent être modélisée comme fluides incompressibles, alors que les gaz ne peuvent pas.
De même, il peut parfois être supposé que la viscosité du fluide est nulle (le fluide est non visqueux). Les gaz peuvent souvent être supposé non visqueux. Si un fluide est visqueux, et son débit contenait une certaine manière (par exemple dans un pipe), alors le flux à la frontière doit avoir une vitesse nulle. Pour un fluide visqueux, si la limite ne est pas poreux, les forces de cisaillement entre le fluide et les résultats dans des limites aussi une vitesse nulle pour le fluide à la limite. Ceci est appelé le condition d'adhérence. Pour un milieu poreux non, à la frontière de la cuve contenant la condition de glissement est pas une vitesse nulle, et le fluide a un champ de vitesse discontinue entre le fluide et le liquide libre dans le milieu poreux (ce qui est lié à la Beavers et Joseph état).
L'hypothèse de continuum
Les liquides sont composées de molécules qui entrent en collision avec l'autre et des objets solides. L'hypothèse de continuum, cependant, considère fluides à continue. Ce est, propriétés telles que la densité, la pression, la température et la vitesse sont prises pour être bien défini au "infiniment" petits points, définissant une REV (Référence élément de volume), à l'ordre géométrique de la distance entre deux molécules adjacentes fluide. Les propriétés sont supposées varier de façon continue d'un point à un autre, et sont les valeurs moyennes dans le REV. Le fait que le fluide est constitué de molécules discrètes est ignorée.
L'hypothèse de continuum est fondamentalement un rapprochement, de la même façon planètes sont approchées par des particules ponctuelles lorsqu'il se agit de la mécanique céleste, et permet donc de solutions approximatives. Par conséquent, hypothèse de l'hypothèse de continuum peut conduire à des résultats qui ne sont pas de précision souhaitées. Cela dit, dans les bonnes circonstances, l'hypothèse du continu produit des résultats extrêmement précis.
Ces problèmes pour lesquels l'hypothèse du continu ne permet pas de solutions de précision souhaitée sont résolues en utilisant la mécanique statistique . Pour déterminer si oui ou non d'utiliser la dynamique des fluides classiques ou mécanique statistique, la Nombre de Knudsen est évaluée pour le problème. Le nombre de Knudsen est défini comme le rapport entre le moléculaire longueur moyenne des parcours libre à une certaine longueur physique représentant échelle. Cette échelle de longueur peut être, par exemple, le rayon d'un corps dans un fluide. (Plus simplement, le nombre de Knudsen est combien de fois son propre diamètre d'une particule se rendra en moyenne avant de frapper une autre particule). Problèmes avec des nombres de Knudsen égales ou supérieures à l'unité sont mieux évaluées en utilisant la mécanique statistique des solutions fiables.
Article détaillé: équations de Navier-Stokes
Les équations de Navier-Stokes (nommés d'après Claude-Louis Navier et George Gabriel Stokes) sont l'ensemble d'équations qui décrivent le mouvement de substances fluides tels que les liquides et les gaz. Ces équations état que des changements dans la dynamique ( accélération ) de particules de fluide ne dépendent que de l'externe pression et forces visqueuses internes (similaire à frottement) agissant sur le fluide. Ainsi, les équations de Navier-Stokes décrivent l'équilibre des forces agissant sur une région donnée du fluide.
Les équations de Navier-Stokes sont des équations différentielles qui décrivent le mouvement d'un fluide. Ces équations établir des relations entre les taux de modifier les variables d'intérêt. Par exemple, les équations de Navier-Stokes pour un fluide avec une viscosité idéale de zéro indique que l'accélération (le taux de variation de vitesse) est proportionnelle à la dérivée de la pression interne.
Cela signifie que les solutions des équations de Navier-Stokes pour un problème physique donné doivent être recherchées à l'aide de calculs . En termes pratiques, seuls les cas les plus simples peuvent être résolus exactement de cette manière. Ces cas impliquent généralement non turbulent, flux constant (débit ne change pas avec le temps) dans lequel le Nombre de Reynolds est petite.
Pour les situations plus complexes, tels que les systèmes météorologiques mondiaux comme El Niño ou l'ascenseur dans une aile, des solutions des équations de Navier-Stokes ne peuvent actuellement être trouvés avec l'aide d'ordinateurs. Ce est un domaine des sciences par son propre appelé dynamique des fluides computationnelle.
Forme générale de l'équation
La forme générale des équations de Navier-Stokes pour la conservation du moment est:
où
 est la densité du fluide,
est la densité du fluide,
 est le dérivé de fond (également appelé le dérivé du matériel)
est le dérivé de fond (également appelé le dérivé du matériel)
 est le vecteur de vitesse,
est le vecteur de vitesse, 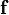 est le vecteur de force de corps, et
est le vecteur de force de corps, et  est un tenseur qui représente les forces de surface appliqués sur une particule fluide (la comobiles tenseur).
est un tenseur qui représente les forces de surface appliqués sur une particule fluide (la comobiles tenseur).
À moins que le fluide est constitué de filage degrés de liberté comme tourbillons,  est un tenseur symétrique. En général, (en trois dimensions)
est un tenseur symétrique. En général, (en trois dimensions)  a la forme:
a la forme:
où
 sont contraintes normales et
sont contraintes normales et  sont contraintes tangentielles (contraintes de cisaillement).
sont contraintes tangentielles (contraintes de cisaillement).
Ce qui précède est en fait un ensemble de trois équations, par une dimension. En eux-mêmes, ceux-ci ne sont pas suffisantes pour produire une solution. Cependant, l'ajout de conservation de la masse et des conditions aux limites appropriées pour le système d'équations produit un ensemble d'équations résoluble.
Fluides newtoniens vs non-newtoniens
Un fluide newtonien (nommé d'après Isaac Newton ) est défini comme étant un fluide dont la contrainte de cisaillement est linéairement proportionnelle à la vitesse gradient dans la direction perpendiculaire au plan de cisaillement. Cette définition signifie indépendamment des forces agissant sur un fluide, il continue à se écouler. Par exemple, l'eau est un fluide newtonien, car il continue à afficher les propriétés des fluides peu importe combien il est agité ou mélangé. Une définition un peu moins rigoureuse est que le traînée d'un petit objet est déplacé à travers le fluide est proportionnelle à la force appliquée à l'objet. (Comparez frottement).
En revanche, en remuant une fluide non-newtonien peut laisser un "trou" derrière. Ce sera progressivement remplir au fil du temps - ce comportement est vu dans des matériaux tels que le pudding, oobleck ou sable (bien que le sable ne est pas strictement un fluide). alternativement, en remuant un fluide non-newtonien peut causer la viscosité de diminuer, de sorte que le fluide apparaît "plus mince" (cela se voit dans la non-goutte peintures). Il existe de nombreux types de fluides non-newtoniens, comme ils sont définis pour être quelque chose qui ne obéit pas à une propriété particulière.
Équations pour un fluide newtonien
La constante de proportionnalité entre la contrainte de cisaillement et le gradient de vitesse est connu comme le viscosité. Une équation simple pour décrire le comportement de fluide newtonien est
où
 est la contrainte de cisaillement exercée par le fluide (" glisser ")
est la contrainte de cisaillement exercée par le fluide (" glisser ")  est la viscosité du fluide - une constante de proportionnalité
est la viscosité du fluide - une constante de proportionnalité  est le gradient de vitesse perpendiculaire à la direction de cisaillement
est le gradient de vitesse perpendiculaire à la direction de cisaillement
Pour un fluide newtonien, la viscosité, par définition, ne dépend que de la température et la pression, pas sur les forces qui agissent sur lui. Si le fluide est incompressible et la viscosité est constante à travers le fluide, l'équation régissant la contrainte de cisaillement (en coordonnées cartésiennes ) est
où
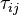 est la contrainte de cisaillement sur la
est la contrainte de cisaillement sur la  face d'un élément dans le fluide
face d'un élément dans le fluide  direction
direction  est la vitesse de la
est la vitesse de la  direction
direction 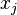 est le
est le  direction coordonnée
direction coordonnée
Si un fluide ne obéit pas à cette relation, il est appelé fluide non newtonien, dont il existe plusieurs types.