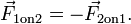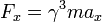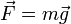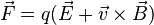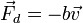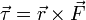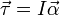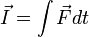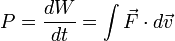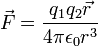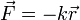Force
Renseignements généraux
Cette sélection écoles a été choisi par SOS Enfants pour les écoles dans le monde en développement ne ont pas accès à Internet. Il est disponible en téléchargement intranet. Parrainer un enfant de faire une réelle différence.

| Chercher vigueur dans Wiktionary, le dictionnaire libre. |
Dans la physique , la force est ce qui provoque une masse à accélérer et est vécue comme une poussée ou une traction. La somme vectorielle de toutes les forces agissant sur un corps (connu sous le nom force nette ou force résultante) est proportionnelle à l'accélération et la masse du corps. Dans un corps étendu, la force peut aussi causer rotation, déformation, ou un changement de pression. Effets de rotation sont déterminés par le couples, tandis que la déformation et la pression sont déterminées par la souligne que les forces créent.
La force nette est mathématiquement identique au temps taux de changement de la dynamique du corps sur lequel il agit. Depuis l'élan est un vecteur quantité (ce est à dire, il a à la fois une ampleur et direction), la force est également une quantité de vecteur.
Le concept de la force a été utilisée dans Statique et dynamique depuis les temps anciens. Ce qui est connu sur les anciennes contributions à la statique est généralement dit avoir culminé avec le travail de Archimède dans le 3ème siècle avant JC, qui fait toujours partie de la physique moderne. En revanche, d'Aristote la dynamique incorporés malentendus intuitives du rôle de la force qui ont finalement été corrigé dans le 17ème siècle culminant dans le travail de Isaac Newton . Suite au développement de la mécanique quantique et de la modèle standard de la physique des particules , il est désormais entendu que les forces associées à des changements dans la dynamique de particules sont la conséquence de interactions fondamentales qui accompagnent l'émission ou l'absorption de bosons de jauge. Sur les grandes échelles, les forces sont perçus avec plus de précision attribuable à la courbure de espace-temps comme explicité dans Einstein de la théorie de la relativité générale . En la physique moderne, seulement quatre interactions fondamentales sont connus; par ordre décroissant de force, ils sont les suivants: [force forte | strong]], électromagnétique , faible, et gravitationnelle. physique des particules de haute énergie observations dans années 1970 et 1980 ont confirmé que les forces faible et électromagnétique sont des expressions d'un unifiée l'interaction électrofaible.
Concepts pré-newtoniens

De l'Antiquité, la notion de force a été reconnue comme partie intégrante du fonctionnement de chacun des machines simples. Le avantage mécanique donnée par une machine simple permis de moins de force pour être utilisé en échange de cette force agissant sur une distance plus grande. L'analyse des caractéristiques des forces en tant que tels, finalement abouti dans le travail de Archimède qui était surtout célèbre pour la formulation d'un traitement de les forces de flottabilité inhérents à fluides.
Philosophique développement du concept d'une force procédé grâce au travail de Aristote . En Cosmologie Aristotleian, le monde naturel a tenu quatre éléments qui existaient dans "état naturel". Aristote croyait que ce était l'état naturel des objets massifs sur la Terre , comme l'eau et la terre éléments, être immobile sur le sol et qu'ils tend vers cet état il est laissé seul. Il distingue entre la tendance innée d'objets à trouver leur «lieu naturel» (par exemple, pour les organismes lourdes pour tomber), qui conduisent à "mouvement naturel", et le mouvement naturel ou forcé, qui exigeaient l'application continue d'une force. Cette théorie, basée sur l'expérience quotidienne de la façon dont les objets se déplacent, tels que l'application constante d'une force nécessaire pour garder un panier mobile, avait de la difficulté conceptuelle représentant le comportement des projectiles, tels que le vol des flèches.
Ces lacunes ne seraient pas entièrement expliqués et corrigés avant que les travaux du XVIIe siècle de Galileo Galilei , qui a été influencé par le regretté idée médiévale que les objets en mouvement forcé effectué une force innée de élan. Galileo construit une expérience dans laquelle des pierres et des boulets de canon ont été à la fois roulé sur une pente de réfuter la Théorie aristotélicienne du mouvement au début du 17ème siècle . Il a montré que les corps ont été accélérées par gravité dans une mesure qui est indépendante de leur masse et soutenu que les objets conservent leur vitesse à moins sollicité par une force, par exemple friction.
Mécanique newtonienne
Isaac Newton est reconnue comme la première personne à plaider explicitement qu'une force constante entraîne un taux constant de changement ( dérivée de temps) de l'élan. En substance, il a donné la première, et la seule définition mathématique de la force - que la dérivée de l'élan: 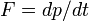 . En 1687, Newton a continué à publier son Philosophiae Naturalis Principia Mathematica , qui a utilisé les concepts de l'inertie, la force et conservation pour décrire le mouvement de tous les objets.
. En 1687, Newton a continué à publier son Philosophiae Naturalis Principia Mathematica , qui a utilisé les concepts de l'inertie, la force et conservation pour décrire le mouvement de tous les objets.

Dans Principia Mathematica , Newton a énoncé trois lois du mouvement qui ont un intérêt direct à la façon dont les forces sont décrits dans la physique.
Première loi de Newton
Première loi du mouvement de Newton énonce les conditions requises pour l'équilibre et définit la inertie liée à la masse d'un objet. En lieu et place de l'idée aristotélicienne de "état naturel", Newton a proposé que ce était le manque de force nette qui était «l'état naturel» fondamentale. Ceci implique directement que l'état de vitesse constante, que ce soit à zéro ou différent de zéro, est le "état" de tous les objets massifs. Objets continuent de se déplacer dans un état de vitesse constante à moins sollicité par une force extérieure déséquilibrée. Dans le prolongement des travaux de Galileo, le concept d'inertie est inexorablement connecté à la notion de vitesses relatives. Plus précisément, dans les systèmes à deux corps, il est impossible de déterminer quel objet est «en mouvement» et qui objet est «au repos»; il est équivalent à basculer entre ce qu'on appelle en physique "inertiel cadres de référence ".
Le concept d'inertie peut encore être généralisée pour expliquer la tendance des objets à poursuivre dans de nombreuses formes différentes de mouvement constant, même ceux qui ne sont pas strictement vitesse constante. Le inertie de rotation de la Terre est ce qui fixe la constance de la durée d'un jour et la longueur d'un années. Albert Einstein a étendu le principe d'inertie plus loin quand il a expliqué que les cadres soumis à une accélération constante de référence, tels que ceux en chute libre vers un objet gravitant, étaient physiquement équivalente aux cadres de référence inertiels. Ce est pourquoi, par exemple, les astronautes expérience apesanteur quand en chute libre orbite autour de la Terre, et pourquoi les lois du mouvement de Newton sont plus facilement perceptibles dans de tels environnements. Si un astronaute place un objet massif dans les airs à côté de elle-même, il restera fixe par rapport à l'astronaute en raison de son inertie. Ce est la même chose qui se produirait si l'astronaute et l'objet massif étaient dans l'espace intergalactique sans force nette de gravité agissant sur leur cadre de référence partagé. Cette principe d'équivalence a été l'un des fondements fondamentaux pour le développement de sa théorie de la relativité générale .
La deuxième loi de Newton
Force est souvent définie en utilisant la deuxième loi de Newton , comme le produit de masse  multipliée par l'accélération
multipliée par l'accélération  :
:
parfois appelé la «deuxième formule la plus célèbre de la physique". Newton n'a jamais dit explicitement la formule = ma F pour laquelle il est souvent crédité. La deuxième loi de Newton est décrit dans ses Principia Mathematica comme un vecteur équation différentielle :
où 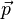 est la dynamique du système. Force est le taux de changement de dynamique dans le temps. L'accélération est le taux de variation de vitesse au fil du temps. Ce résultat, qui suit en tant que conséquence directe de la mise en garde dans la première loi de Newton, montre que la croyance aristotélicienne intuitive qu'une force nette est nécessaire pour maintenir un objet se déplaçant à vitesse constante (zéro d'accélération donc) est objectivement mal et pas seulement la conséquence d'un mauvais choix de définition.
est la dynamique du système. Force est le taux de changement de dynamique dans le temps. L'accélération est le taux de variation de vitesse au fil du temps. Ce résultat, qui suit en tant que conséquence directe de la mise en garde dans la première loi de Newton, montre que la croyance aristotélicienne intuitive qu'une force nette est nécessaire pour maintenir un objet se déplaçant à vitesse constante (zéro d'accélération donc) est objectivement mal et pas seulement la conséquence d'un mauvais choix de définition.
L'utilisation de la deuxième loi de Newton dans l'une de ces formes comme une définition de la force a été décriée dans certains des manuels plus rigoureuses, car cela supprime tout contenu empirique de la loi. En fait, la  dans cette équation représente la force nette (somme vectorielle); en équilibre ce est nul par définition, mais les forces (équilibrés) sont présents néanmoins. Au lieu de cela, la deuxième loi de Newton affirme seulement la proportionnalité de l'accélération et de la masse à la force, dont chacun peut être défini sans référence explicite aux forces. Accélérations peuvent être définies par des mesures cinématiques en masse peut être déterminée par le biais, par exemple, compter les atomes. Cependant, alors que la cinématique sont bien décrits par analyse du cadre de référence en physique avancée, il ya encore des questions profondes qui restent à ce qui est la définition correcte de la masse. La relativité générale propose une équivalence entre espace-temps et de la masse, mais il manque une théorie cohérente de la gravité quantique, il est difficile de savoir comment ou si cette connexion est pertinente sur microbalance. Avec un peu plus de justification, la deuxième loi de Newton peut être considéré comme une définition quantitative de la masse en écrivant la loi comme une égalité, les unités relatives de force et de masse sont fixés.
dans cette équation représente la force nette (somme vectorielle); en équilibre ce est nul par définition, mais les forces (équilibrés) sont présents néanmoins. Au lieu de cela, la deuxième loi de Newton affirme seulement la proportionnalité de l'accélération et de la masse à la force, dont chacun peut être défini sans référence explicite aux forces. Accélérations peuvent être définies par des mesures cinématiques en masse peut être déterminée par le biais, par exemple, compter les atomes. Cependant, alors que la cinématique sont bien décrits par analyse du cadre de référence en physique avancée, il ya encore des questions profondes qui restent à ce qui est la définition correcte de la masse. La relativité générale propose une équivalence entre espace-temps et de la masse, mais il manque une théorie cohérente de la gravité quantique, il est difficile de savoir comment ou si cette connexion est pertinente sur microbalance. Avec un peu plus de justification, la deuxième loi de Newton peut être considéré comme une définition quantitative de la masse en écrivant la loi comme une égalité, les unités relatives de force et de masse sont fixés.
La définition de la force est parfois considérée comme problématique, car il doit soit finalement renvoyé à notre compréhension intuitive de nos perceptions directes, ou être définie implicitement par un ensemble de formules mathématiques cohérentes. Physiciens notables, des philosophes et des mathématiciens qui ont cherché une définition plus explicite comprennent Ernst Mach, Clifford et Truesdell Walter Noll.
Étant donné le succès empirique de la loi de Newton, il est parfois utilisé pour mesurer la puissance des forces (par exemple, utilisant des orbites astronomiques pour déterminer les forces gravitationnelles). Néanmoins, la force et les quantités utilisées pour mesurer restent des concepts distincts.
Quand une résultante force agit sur un objet de masse constante, une accélération se traduira par le produit de sa masse et de l'accélération égale à la force résultante, la direction de l'accélération étant dans la même direction que celle de la force résultante. F = ma '
La troisième loi de Newton
La troisième loi de Newton est un résultat de l'application symétrie situations où les forces peuvent être attribués à la présence de différents objets. Pour deux objets (appelez-les 1 et 2), la troisième loi de Newton affirme que
Cette loi implique que les forces se produisent toujours par paires action-réaction. Toute force qui est appliquée à opposer une due à l'action de l'objet 2 est automatiquement accompagnée d'une force appliquée à opposer deux en raison de l'action de l'objet 1. Si l'objet 1 et l'objet deux sont considérés comme dans le même système, le force nette sur le système en raison des interactions entre les objets 1 et 2 est nul car
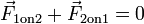 .
.
Cela signifie que les systèmes ne peuvent pas créer forces internes qui sont déséquilibrés. Toutefois, si les objets 1 et 2 sont considérées comme dans des systèmes séparés, puis les deux systèmes seront Chaque expérience une force déséquilibrée et accélérer par rapport à l'autre en fonction de la deuxième loi de Newton.
Combinant deuxième et troisième lois de Newton, il est possible de montrer que la quantité de mouvement d'un système est conservée . Utilisation
et l'intégration par rapport au temps, l'équation:
est obtenu. Pour un système qui inclut des objets 1 et 2,
qui est la conservation de la quantité de mouvement. La généralisation à un système d'un nombre arbitraire de particules est simple. Cela montre que l'échange dynamique entre les objets constitutifs ne affectera pas l'impulsion nette d'un système. En général, tant que toutes les forces sont dues à l'interaction des objets massifs, il est possible de définir un système tel que l'élan net ne est jamais perdu ni gagné.
«Si un corps exerce une force F sur le corps B, puis B corps exerce une force de -F (de taille égale, mais en sens inverse) sur le corps A. '
Descriptions
Forces peuvent être directement perçues comme pousse ou tire; ce qui peut fournir un cadre pour décrire les forces intuitive. Comme avec d'autres concepts physiques (par exemple de température ), la notion intuitive est quantifiée à l'aide définitions opérationnelles qui sont conformes à la perception directe, mais sont plus précis (voir la section sur la mécanique newtonienne pour savoir comment cela se fait ). Historiquement, les forces ont d'abord été étudiés quantitativement dans des conditions de équilibre statique lorsque plusieurs forces mutuellement annulées. Ces expériences prouvent les propriétés cruciales que les forces sont additives vecteur quantités: ils ont ampleur et direction. Lorsque deux forces agissent sur un objet, la force résultante, la résultante, est la somme vectorielle des forces d'origine. Ceci est appelé le principe de superposition. L'ampleur de la résultante varie de la différence des amplitudes des deux forces à leur somme, en fonction de l'angle entre leurs lignes d'action. La force résultante peut être déterminée en suivant le règle de parallélogramme de l'addition de vecteur: l'ajout de deux vecteurs représentés par des côtés d'un parallélogramme, donne un vecteur résultant équivalent qui est égale en grandeur et direction à la transversale du parallélogramme.
Diagrammes de corps libres peuvent être utilisés comme un moyen pratique de garder une trace des forces agissant sur un système. Idéalement, ces diagrammes sont dessinés avec les angles et les amplitudes relatives des vecteurs de force conservé de sorte que l'addition de vecteurs graphique peut être effectuée afin de déterminer la résultante.
En plus d'être ajoutée, les forces peuvent également être résolus en composantes indépendantes à angle droit par rapport à l'autre. Une force horizontale pointant nord peut donc être divisé en deux forces, l'une pointant vers le nord, et un pointage est. La somme de ces composants à l'aide de forces addition de vecteurs donne la force originale. Résoudre les vecteurs de force dans les composants d'un ensemble de vecteurs de base est souvent une façon plus propre à décrire mathématiquement forces que d'utiliser grandeurs et les directions. Ce est parce que, pour composantes orthogonales, les composantes de la somme vectorielle est déterminée de façon unique par l'addition scalaire des composantes des vecteurs individuels. Composantes orthogonales sont indépendants les uns des autres; forces agissant à quatre vingt dix degrés à l'autre ne ont aucun effet sur l'autre. Le choix d'un ensemble de vecteurs de base orthogonales est souvent fait en considérant quel ensemble de vecteurs de base fera les mathématiques plus commode. Le choix d'un vecteur de base qui est dans le même sens que l'une des forces est souhaitable, étant donné que la force aurait alors une seule composante non nulle. des vecteurs de force peut également être en trois dimensions, avec le troisième composant à angle droit par rapport aux deux autres composants.
Equilibres
L'équilibre se produit lorsque la force résultante agissant sur un objet est égale à zéro (ce est la somme vectorielle de toutes les forces est nul). Il existe deux types d'équilibre: équilibre statique et équilibre dynamique.
Équilibre statique
Équilibre statique a été bien compris avant l'invention de la mécanique classique. Objets qui sont au repos ont nulle force nette agissant sur eux.
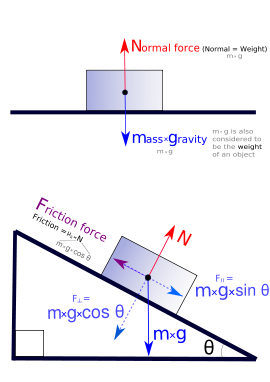
Le cas le plus simple d'équilibre statique se produit lorsque deux forces sont égales en amplitude mais de sens opposé. Par exemple, ne importe quel objet sur une surface de niveau est tiré (attirée) vers le bas vers le centre de la Terre par la force de gravité. Dans le même temps, les forces de surface résister à la force vers le bas avec une force vers le haut égale (appelé le force normale) et le résultat dans l'objet ayant une valeur non nulle poids. La situation est un des zéro et aucune force nette accélération.
Poussant contre un objet sur une surface de friction peut entraîner dans une situation où l'objet ne bouge pas parce que la force appliquée est opposé par frottement statique, généré entre l'objet et la surface de la table. Pour une situation sans mouvement, la force de frottement statique équilibre exactement la force appliquée entraîne pas d'accélération. Les augmentations de frottement statique ou diminue en réponse à la force appliquée jusqu'à une limite supérieure déterminée par les caractéristiques du contact entre la surface et l'objet.
Un équilibre statique entre deux forces est la façon la plus habituelle de mesure des forces, en utilisant des dispositifs simples tels que balances et balances à ressort. Par exemple, un objet suspendu à la verticale balance à ressort éprouve la force de gravité agissant sur l'objet pondérées par une force appliquée par la "force de réaction de printemps» qui est égale au poids de l'objet. L'utilisation de ces outils, certaines lois de force quantitatives ont été découverts: que la force de gravité est proportionnelle au volume pour les objets de constante densité (largement exploitées depuis des millénaires pour définir les poids standard); De principe pour la flottabilité; Archimède Archimède de l'analyse de la levier; La loi de Boyle de pression de gaz; et La loi de Hooke pour les ressorts. Ils ont tous été formulés et expérimentalement vérifiées avant Isaac Newton a exposé ses trois lois du mouvement .
Équilibre dynamique

Équilibre dynamique a été décrite par Galileo qui ont remarqué que certaines hypothèses de la physique aristotélicienne ont été contredites par observations et logique . Galileo est rendu compte que simple addition de vitesse exige que le concept d'une "absolue cadre repos »ne existait pas. Galileo a conclu que le mouvement dans une constante de vitesse était complètement équivalent au repos. Ce est contraire à la notion aristotélicienne d'un "état naturel" de repos que les objets massifs naturellement approché. Des expériences simples montrent que la compréhension de Galileo de l'équivalence de la vitesse et reste constant d'être correcte. Par exemple, si un marin a chuté un boulet de canon du nid de pie d'un navire se déplaçant à une vitesse constante, la physique aristotélicienne aurait le boulet de canon tombe vers le bas alors que le navire déplacé en dessous. Ainsi, un univers aristotélicienne, le boulet de canon tomber allait atterrir derrière le pied du mât d'un navire en mouvement. Toutefois, lorsque cette expérience est effectivement réalisée, le boulet de canon tombe toujours au pied du mât, comme si le boulet de canon sait voyager avec le navire tout en étant séparé de celle-ci. Comme il ne existe aucune force horizontale vers l'avant appliquée sur le boulet de canon comme il tombe, la seule conclusion gauche, ce est que le boulet de canon continue à se déplacer à la même vitesse que le bateau comme il tombe. Ainsi, aucune force ne est nécessaire pour maintenir le boulet de canon se déplaçant à la vitesse d'avance constante.
En outre, ne importe quel objet se déplaçant à une vitesse constante doit être soumis à zéro force nette (de force résultante). Ce est la définition de l'équilibre dynamique: lorsque toutes les forces sur un équilibre de l'objet, mais il se déplace toujours à une vitesse constante.
Un cas simple d'équilibre dynamique se produit en mouvement à vitesse constante sur une surface avec frottement cinétique. Dans une telle situation, une force est appliquée dans la direction de déplacement tandis que la force de frottement cinétique se oppose exactement la force appliquée. Il en résulte une force nette nulle, mais étant donné que l'objet a commencé avec une vitesse non nulle, il continue à se déplacer avec une vitesse non nulle. Aristote mal interprété cette motion comme étant causée par la force appliquée. Toutefois, lorsque frottement cinétique est pris en considération, il est clair qu'il n'y a pas de force nette provoquant un mouvement à vitesse constante.
Diagrammes de Feynman

Forces et l'accélération des particules dans modernes physique des particules se produisent au cours de l'échange de bosons de jauge. Avec le développement de la théorie quantique des champs et de la relativité générale , on a réalisé que «force» est un concept redondant résultant de la conservation du moment ( 4-impulsion dans la relativité et l'élan particules virtuelles dans Électrodynamique quantique). La conservation de l'impulsion, de Théorème de Noether, peut être directement dérivée de la de symétrie l'espace et ainsi est généralement considéré comme plus fondamentale que le concept d'une force. Ainsi, le connu actuellement forces fondamentales sont considérées comme plus précisément d'être " interactions fondamentales ". Bien que les descriptions mathématiques sophistiqués sont nécessaires pour prédire, en détail, la nature de ces interactions, il ya une façon conceptuellement simple pour décrire ces interactions grâce à l'utilisation des diagrammes de Feynman. Dans un diagramme de Feynman, chaque particule de matière est représentée comme une ligne droite (voir ligne d'univers) voyager dans le temps qui augmente normalement vers le haut ou vers la droite dans le diagramme. Les particules de matière et d'antimatière sont identiques, sauf pour leur sens de propagation à travers le diagramme de Feynman. lignes mondiales de particules se croisent à sommets d'interaction et le diagramme de Feynman représente une force résultant d'une interaction comme se produisant au niveau du sommet avec un changement instantané associée dans la direction des lignes d'univers de particules. bosons de jauge sont émis loin du sommet comme des lignes ondulées (similaires aux ondes) et, dans le cas de l'échange de particules virtuelles, sont absorbés à un sommet adjacent. Lorsque les bosons de jauge sont représentées dans un diagramme de Feynman comme existant entre deux particules en interaction, ce qui représente une force de répulsion. Lorsque les bosons de jauge sont représentées dans un diagramme de Feynman comme existant entourant les deux particules en interaction, ce qui représente une force d'attraction.
L'utilité des diagrammes de Feynman est que d'autres types de phénomènes physiques qui font partie de l'image générale de interactions fondamentales mais sont conceptuellement distincte de forces peuvent aussi être décrites en utilisant les mêmes règles. Par exemple, un diagramme de Feynman peut décrire en détail comment une succincte neutrons se désintègre en un électron , proton , et neutrino: une interaction à médiation par la même boson de jauge qui est responsable de la force nucléaire faible. Alors que le diagramme de Feynman pour cette interaction a des caractéristiques similaires à une interaction répulsive, la décroissance est plus compliqué qu'une "force répulsive" simple.
Relativité restreinte
Dans la théorie de la relativité de masse et l'énergie sont équivalentes (comme on peut le voir en calculant le travail nécessaire pour accélérer un corps). Lorsque la vitesse d'un objet augmente il en va de son énergie et donc sa masse équivalente (inertie). Il faut donc plus de force pour accélérer la même quantité que l'a fait à une vitesse inférieure. La définition  reste valable. Mais afin d'être conservée, l'élan doit être redéfinie comme:
reste valable. Mais afin d'être conservée, l'élan doit être redéfinie comme:
où
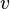 est la vitesse et
est la vitesse et
 est la vitesse de la lumière .
est la vitesse de la lumière .
L'expression relativiste force et l'accélération relative pour une particule non nul avec masse au repos  se déplaçant dans la
se déplaçant dans la 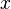 direction est:
direction est:
où le Facteur de Lorentz
Voici une force constante ne produit pas une accélération constante, mais une accélération diminution constante que l'objet se approche de la vitesse de la lumière. Notez que  est undefined pour un objet avec une valeur non nulle masse au repos à la vitesse de la lumière, et la théorie ne donne pas de prévision à cette vitesse.
est undefined pour un objet avec une valeur non nulle masse au repos à la vitesse de la lumière, et la théorie ne donne pas de prévision à cette vitesse.
On peut toutefois restaurer la forme de
pour une utilisation dans la relativité par l'utilisation de les quatre vecteurs. Cette relation est correcte dans la relativité lorsque 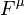 est le quatre vigueur, m est le masse invariante, et
est le quatre vigueur, m est le masse invariante, et  est le quatre-accélération.
est le quatre-accélération.
Modèles fondamentaux
Toutes les forces de l'Univers sont tous basés sur quatre forces fondamentales. Les forces forts et faibles ne agissent que sur de très courtes distances, et sont responsables de la tenue certaine nucléons et composés noyaux ensemble. La force électromagnétique agit entre charges électriques et les actes des forces gravitationnelles entre masses . Tous les autres forces sont basés sur l'existence des quatre interactions fondamentales. Par exemple, friction est une manifestation de la force électromagnétique agissant entre les atomes de deux les surfaces et le principe d'exclusion de Pauli, qui ne permet pas d'atomes de passer à travers l'un l'autre. Les forces modélisé par des ressorts La loi de Hooke sont aussi le résultat de forces électromagnétiques et le principe d'exclusion agissant ensemble pour retourner l'objet à sa position d'équilibre. Les forces centrifuges sont des forces d'accélération qui surgissent simplement à partir de l'accélération de rotation cadres de référence.
Le point de vue de la mécanique quantique moderne des trois premières forces fondamentales (tous sauf gravité) est que les particules de la matière ( fermions) ne interagit pas directement avec l'autre, mais plutôt par un échange de particules virtuelles appelées bosons de jauge.
Ce est une idée fausse très répandue d'attribuer la rigidité et la rigidité de matière solide à la répulsion des charges comme sous l'influence de la force électromagnétique. Toutefois, ces caractéristiques entraînent en fait de la Principe d'exclusion de Pauli. Comme les électrons sont fermions, ils ne peuvent pas occuper le même état mécanique quantique que d'autres électrons. Lorsque les électrons dans un matériau sont densément emballés ensemble, il n'y a pas assez faible énergie quantique états mécaniques pour tous, de sorte que certains d'entre eux doivent être dans des états d'énergie plus élevés. Cela signifie qu'il faut de l'énergie pour les emballer ensemble. Bien que cet effet se manifeste macroscopiquement comme une "force" structurel, il est techniquement seulement le résultat de l'existence d'un ensemble fini d'états d'électrons.
Pesanteur
Ce que nous appelons aujourd'hui la gravité n'a pas été identifié comme une force universelle jusqu'à ce que le travail d'Isaac Newton. Avant Newton, la tendance pour les objets de tomber vers la Terre n'a pas été comprise à être liés aux mouvements des objets célestes. Galileo a contribué à décrire les caractéristiques de la chute d'objets en déterminant que l' accélération de chaque corps chute libre est constante et indépendante de la masse de l'objet. Aujourd'hui, cette accélération de la pesanteur à la surface de la Terre est généralement désigné comme  et a une amplitude d'environ 9,81 mètres par seconde au carré (cette mesure est prise à partir du niveau de la mer et peut varier selon l'endroit), et les points vers le centre de la Terre. Cette observation signifie que la force de gravité sur un objet à la surface de la Terre est directement proportionnelle à la masse de l'objet. Ainsi un objet qui a une masse de
et a une amplitude d'environ 9,81 mètres par seconde au carré (cette mesure est prise à partir du niveau de la mer et peut varier selon l'endroit), et les points vers le centre de la Terre. Cette observation signifie que la force de gravité sur un objet à la surface de la Terre est directement proportionnelle à la masse de l'objet. Ainsi un objet qui a une masse de  subira une force:
subira une force:
En chute libre, cette force ne est pas contestée et donc la force nette sur l'objet est la force de gravité. Pour les objets non en chute libre, la force de gravité est opposé par le poids de l'objet. Par exemple, une personne debout sur le sol subit force nette nulle, car la force de gravité est compensée par le poids de la personne qui se manifeste par une force normale exercée sur la personne par le sol.
La contribution à la théorie de Newton gravitationnelle était d'unifier les mouvements des corps célestes, dont Aristote avait assumées étaient dans un état naturel de mouvement constant, sans tomber mouvement observé sur la Terre. Il a proposé un loi de la gravité qui pourrait expliquer les mouvements célestes qui ont été décrites précédemment en utilisant les lois de Kepler sur le mouvement planétaire .
Newton se est rendu compte que les effets de la gravité peuvent être observés de différentes manières à de plus grandes distances. En particulier, Newton a déterminé que l'accélération de la lune autour de la terre pourrait être attribué à la même force de gravité si l'accélération due à la pesanteur comme une diminution de loi du carré inverse. En outre, Newton est rendu compte que la masse de l'objet gravitant affecté directement l'accélération due à la gravité. La combinaison de ces idées donne une formule qui concerne la masse de la Terre (  ), Le rayon de la Terre (
), Le rayon de la Terre (  ) À l'accélération de la pesanteur:
) À l'accélération de la pesanteur:
où la direction du vecteur est donnée par 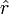 qui est le vecteur unitaire dirigé vers l'extérieur depuis le centre de la Terre.
qui est le vecteur unitaire dirigé vers l'extérieur depuis le centre de la Terre.
Dans cette équation, une constante dimensionnelle 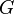 est utilisé pour décrire la force relative de la gravité. Cette constante est venu à être connu sous le nom Universal Gravitation la constante de Newton, si ce ne était d'une valeur inconnue dans la vie de Newton. Pas avant 1798 était Henry Cavendish en mesure de faire la première mesure de
est utilisé pour décrire la force relative de la gravité. Cette constante est venu à être connu sous le nom Universal Gravitation la constante de Newton, si ce ne était d'une valeur inconnue dans la vie de Newton. Pas avant 1798 était Henry Cavendish en mesure de faire la première mesure de 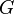 en utilisant un balance de torsion; cela a été largement rapporté dans la presse comme une mesure de la masse de la Terre depuis la connaissance de la
en utilisant un balance de torsion; cela a été largement rapporté dans la presse comme une mesure de la masse de la Terre depuis la connaissance de la 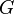 pourrait permettre de résoudre une pour la masse de la Terre étant donné l'équation ci-dessus. Newton, cependant réalisé que puisque tous les corps célestes suivent les mêmes lois du mouvement , sa loi de gravité devait être universelle. Dit succinctement, Loi de Newton de la gravitation entre deux corps massifs est
pourrait permettre de résoudre une pour la masse de la Terre étant donné l'équation ci-dessus. Newton, cependant réalisé que puisque tous les corps célestes suivent les mêmes lois du mouvement , sa loi de gravité devait être universelle. Dit succinctement, Loi de Newton de la gravitation entre deux corps massifs est
où 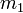 est la masse du premier objet et
est la masse du premier objet et 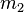 est la masse du second objet.
est la masse du second objet.
Cette formule était assez puissant pour se présenter comme la base de toutes les descriptions suivantes du mouvement dans le système solaire jusqu'au XXe siècle. Pendant ce temps, des méthodes sophistiquées de l'analyse des perturbations ont été inventés pour calculer les écarts de orbites en raison de l'influence de multiples organismes sur une planète , lune , comète ou un astéroïde . Ces techniques sont si puissants qu'ils peuvent être utilisés pour prédire avec précision le mouvement des corps célestes à une précision arbitraire à ne importe quelle longueur de temps dans l'avenir. Le formalisme est assez exacte pour permettre mathématiques pour prédire l'existence de la planète Neptune avant qu'il ne soit observée.
Ce ne est que l'orbite de la planète Mercure que la loi de la gravitation de Newton semblait pas à expliquer entièrement. Certains astrophysiciens prédit l'existence d'une autre planète ( Vulcan) qui pourrait expliquer les écarts; Toutefois, en dépit de quelques premières indications, aucune planète n'a pu être trouvée. Lorsque Albert Einstein a finalement formulé sa théorie de la relativité générale (GR), il tourna son attention sur le problème de l'orbite de Mercure et a constaté que sa théorie ajouté une correction qui pourrait expliquer la différence. Ce était la première fois que la théorie de la gravitation de Newton avait été montré à être moins bonne qu'une alternative.
Depuis lors, et jusqu'à présent, la relativité générale a été reconnue comme la théorie qui explique le mieux la gravité. En GR, la gravitation ne est pas considérée comme une force, mais plutôt, des objets en mouvement librement dans les champs gravitationnels voyager sous leur propre inertie lignes droites à travers l'espace-temps courbé - défini comme le chemin le plus court espace-temps entre deux événements espace-temps. Du point de vue de l'objet, tout mouvement se passe comme si il n'y avait pas la gravitation que ce soit. Ce est seulement quand observant le mouvement dans un sens global que la courbure de l'espace-temps peut être observée et la force est déduite de trajectoire courbe de l'objet. Ainsi, le trajet en ligne droite dans l'espace-temps est considéré comme une ligne courbe dans l'espace, et il est appelé le balistique la trajectoire de l'objet. Par exemple, un basket jeté depuis le sol se déplace dans un parabole, car il est dans un champ gravitationnel uniforme. Sa trajectoire spatio-temporel (lorsque la dimension supplémentaire est ajoutée ct) est une ligne presque droite, légèrement incurvée (avec le rayon de courbure de l'ordre de quelques Années lumière). La dérivée temporelle de la dynamique de l'évolution corps est ce que nous appelons aussi "force gravitationnelle".
Les forces électromagnétiques
En 1784 Charles Coulomb a découvert la loi du carré inverse de l'interaction entre les charges électriques en utilisant une balance de torsion; ce fut la deuxième force fondamentale. Les forces faibles et forts ont été découverts dans le 20ème siècle par le développement de la physique nucléaire .
La force électrostatique a été décrite pour la première en 1784 par Coulomb comme une force qui existait intrinsèque entre deux charges . Les propriétés de la force électrostatique étaient qu'il varie comme une loi du carré inverse dirigé dans la direction radiale , était à la fois attractive et répulsive (il était intrinsèque polarité), était indépendante de la masse des objets chargés, et a suivi la loi de superposition. Unifier toutes ces observations dans un exposé succinct est devenu connu comme la loi de Coulomb .
Mathématiciens et physiciens ultérieures ont trouvé la construction du champ électrique pour être utile pour déterminer la force électrostatique sur une charge électrique à tout point de l'espace. Basé sur la loi de Coulomb, connaissant les caractéristiques du champ électrique dans un espace donné est équivalente à savoir ce que la force électrostatique appliquée sur une " charge de test "est.
Pendant ce temps, la connaissance a été développé de la force de Lorentz de magnétisme , la force qui existe entre deux des courants électriques. Il a le même caractère mathématique en tant que loi de Coulomb à la condition que, comme les courants attirent et repoussent contrairement courants. Comme pour le champ électrique, le champ magnétique peut être utilisé pour déterminer la force magnétique sur un courant électrique à un point quelconque dans l'espace. La combinaison de la définition du courant électrique que le taux de temps de changement de charge électrique donne une loi de multiplication vectorielle appelé loi de Lorentz qui détermine la force sur le déplacement dans un champ magnétique d'une charge.
Ainsi une théorie complète de la force électromagnétique sur une charge peut être écrit comme la somme de la force électrostatique (due au champ électrique) et la force magnétique (due au champ magnétique). Entièrement déclaré, telle est la loi:
où  est la force électromagnétique,
est la force électromagnétique,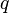 est la grandeur de la charge de la particule,
est la grandeur de la charge de la particule, est lavitessede la particule,
est lavitessede la particule, est le champ électrique et
est le champ électrique et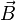 le champ magnétique est.
le champ magnétique est.
L'origine des champs électriques et magnétiques ne serait pas entièrement expliqué jusqu'en 1864 quand James Clerk Maxwell a unifié un certain nombre de théories antérieures en un ensemble succincte de quatre équations. Ces « Equations de Maxwell "décrit complètement les sources des champs comme étant stationnaire et charges en mouvement, et les interactions des champs eux-mêmes. Cela a conduit à découvrir que Maxwell champs électriques et magnétiques pourraient être «auto-génération" à travers une vague qui se déplaçait à une vitesse qui il a calculé pour être le vitesse de la lumière . Cette idée a uni les domaines naissants de la théorie électromagnétique avec l'optique et conduit directement à une description complète de la spectre électromagnétique.
Cependant, la tentative de réconcilier la théorie électromagnétique avec deux observations, l' effet photoélectrique, et l'inexistence de la catastrophe ultraviolette, révélée gênante. Grâce au travail des physiciens théoriques principaux, une nouvelle théorie de l'électromagnétisme a été développé en utilisant la mécanique quantique . Cette modification finale de la théorie électromagnétique a finalement abouti à l'électrodynamique quantique (ou QED), qui décrit en détail tous les phénomènes électromagnétiques comme étant médiée par des particules connues sous le nom d'onde des photons . Dans CQFD, les photons sont les particules de change fondamental qui décrit toutes les interactions liées à l'électromagnétisme, y compris la force électromagnétique.
Les forces nucléaires
Il ya deux «forces nucléaires" qui, aujourd'hui, sont généralement décrits comme des interactions qui ont lieu dans les théories quantiques dela physique des particules. Le force nucléaire forte est la force responsable de l'intégrité structurelle desnoyaux atomiquestandis que laforce nucléaire faible est responsable de la désintégration de certainsnucléons dansles leptons et d'autres types dehadrons.
La force forte est aujourd'hui compris pour représenter les interactions entre les quarks et les gluons comme détaillé par la théorie de la chromodynamique quantique (QCD). La force forte est la force fondamentale médiée par les gluons, agissant sur les quarks , les antiquarks, et les gluons eux-mêmes. L'interaction forte est le plus puissant des quatre forces fondamentales.
La force forte agit seulement directement sur les particules élémentaires. Toutefois, un résidu de la force est observée entre hadrons (l'exemple le plus connu étant la force qui agit entre les nucléons dans les noyaux atomiques) que les force nucléaire. Voici les actes de force fortes indirectement, transmis que des gluons qui font partie de la pi virtuelle et rho mésons qui transmettre classiquement la force nucléaire (voir à ce sujet pour plus). L'échec de nombreuses recherches pour quarks libres a montré que les particules élémentaires touchées sont pas directement observables. Ce phénomène est appelé couleur confinement.
La force faible est due à l'échange des lourds bosons W et Z. Son effet le plus courant est la désintégration bêta (de neutrons dans les noyaux atomiques ) et l'associé la radioactivité. Le mot «faible» provient du fait que l'intensité du champ est environ 10 13 fois inférieure à celle de la force forte. Pourtant, il est plus fort que la gravité sur de courtes distances. Un cohérente théorie électrofaible a également été développé qui montre que les forces électromagnétiques et la force faible sont indiscernables à un des températures supérieures à environ 10 15 Kelvin . Ces températures ont été sondés dans modernes accélérateurs de particules et de montrer les conditions de l' univers dans les premiers moments de la Big Bang .
Les modèles non-fondamentaux
Certaines forces peuvent être modélisées en faisant des hypothèses simplificatrices sur les conditions physiques. Dans de telles situations, des modèles idéalisés peuvent être utilisés pour mieux comprendre physique.
Force normale

La force normale est la force de surface qui agit perpendiculairement à la surface interface entre les deux objets. La force normale, par exemple, est responsable de l'intégrité structurale de tables et les planchers ainsi que d'être la force qui répond chaque fois une force externe pousse sur un objet solide. Un exemple de la force normale en action est la force d'un objet écraser sur une surface immobile d'impact. Cette force est proportionnelle au carré de la vitesse de l'objet en raison de la conservation de l'énergie et du théorème de l'énergie de travail lorsqu'il est appliqué à tout collisions inélastiques.
Friction
Le frottement est une force de surface qui oppose le mouvement. La force de frottement est directement liée à la force normale qui agit pour maintenir deux objets solides séparées au point de contact. Il existe deux grandes catégories de forces de frottement: frottement statique et frottement cinétique.
La force de frottement statique ( ) sera exactement opposer forces appliquées à un organisme parallèle à une surface de contact jusqu'à la limite spécifiée par lecoefficient de frottement statique (
) sera exactement opposer forces appliquées à un organisme parallèle à une surface de contact jusqu'à la limite spécifiée par lecoefficient de frottement statique ( ) multiplié par la force normale (
) multiplié par la force normale (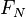 ).En d'autres termes l'ampleur des statiques satisfait de la force de frottement du l'inégalité:
).En d'autres termes l'ampleur des statiques satisfait de la force de frottement du l'inégalité:
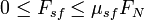 .
.
La force de frottement cinétique ( 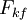 ) est indépendant des deux forces appliquées et le mouvement de l'objet. Ainsi, la grandeur de la force est égale à
) est indépendant des deux forces appliquées et le mouvement de l'objet. Ainsi, la grandeur de la force est égale à
 ,
,
où  est le coefficient de friction cinétique. Pour la plupart des interfaces de surface, le coefficient de frottement cinétique inférieur au coefficient de frottement statique.
est le coefficient de friction cinétique. Pour la plupart des interfaces de surface, le coefficient de frottement cinétique inférieur au coefficient de frottement statique.
Mécanique des milieux continus
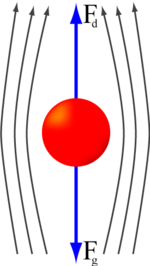
 ) associée à la résistance de l'air devient égale en amplitude à la force de gravité sur un objet qui tombe (
) associée à la résistance de l'air devient égale en amplitude à la force de gravité sur un objet qui tombe ( ), l'objet atteint un état d'équilibre dynamiqueàvitesse terminale.
), l'objet atteint un état d'équilibre dynamiqueàvitesse terminale.Dans étenduesliquides, les différences derésultat de la pression dans les forces dirigé le long, la pressiongradients comme suit:
où 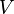 est le volume de l'objet dans le liquide et
est le volume de l'objet dans le liquide et 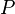 est le la fonction scalaire qui décrit la pression au niveau de tous les emplacements dans l'espace. gradients de pression et des écarts résultent de la force de flottabilité pour les fluides en suspension dans les champs gravitationnels, les vents en sciences de l'atmosphère, et l' ascenseur associés à l'aérodynamique et vol.
est le la fonction scalaire qui décrit la pression au niveau de tous les emplacements dans l'espace. gradients de pression et des écarts résultent de la force de flottabilité pour les fluides en suspension dans les champs gravitationnels, les vents en sciences de l'atmosphère, et l' ascenseur associés à l'aérodynamique et vol.
Un exemple spécifique d'une telle force qui est associée àla pression dynamique est la résistance de fluide: une force de corps qui résiste au mouvement d'un objet dans un fluide en raison de viscosité.Pour soi-disant "glisser de Stokes "la force est approximativement proportionnelle à la vitesse, mais en sens opposé:
où:
 est une constante qui dépend des propriétés du fluide et les dimensions de l'objet (en général lazone de coupe transversale), et
est une constante qui dépend des propriétés du fluide et les dimensions de l'objet (en général lazone de coupe transversale), et est la vitesse de l'objet.
est la vitesse de l'objet.
Plus formellement, les forces enmécanique des milieux continus sont entièrement desribed par un stress tenseur avec des termes qui sont définis comme peu prés
où 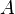 est l'aire en coupe transversale correspondant au volume pour lequel le tenseur de contrainte est calculé. Ce formalisme comprend des termes de pression associés à des forces qui agissent perpendiculairement à la surface de section transversale (les diagonales de la matrice du tenseur) ainsi que les conditions de cisaillement associés à des forces qui agissent parallèlement à la surface de section transversale (les éléments hors diagonale). Représente le tenseur de stress pour les forces qui causent tous les déformations y compris aussi les contraintes et traction compressions.
est l'aire en coupe transversale correspondant au volume pour lequel le tenseur de contrainte est calculé. Ce formalisme comprend des termes de pression associés à des forces qui agissent perpendiculairement à la surface de section transversale (les diagonales de la matrice du tenseur) ainsi que les conditions de cisaillement associés à des forces qui agissent parallèlement à la surface de section transversale (les éléments hors diagonale). Représente le tenseur de stress pour les forces qui causent tous les déformations y compris aussi les contraintes et traction compressions.
Tension
les forces de tension peut être idéalisées utilisant cordes idéales qui sont sans masse, sans frottement, incassable, et non extensible. Ils peuvent être combinés avec idéales poulies qui permettent cordes idéales pour basculer direction physique. Cordes Idéal transmettent les forces de tension instantanément par paires action réaction de sorte que si deux objets sont reliés par une chaîne idéal, toute force dirigée le long de la chaîne par le premier objet est accompagné par une force dirigée le long de la chaîne dans la direction opposée par le second objet . En connectant la même chaîne plusieurs fois pour le même objet par l'utilisation d'un set-up qui utilise poulies mobiles, la force de tension sur une charge peut être multiplié. Pour chaque chaîne qui agit sur une charge, un autre facteur de la force de tension de la corde agit sur la charge. Cependant, même si ces machines permettent une augmentation de la force, il existe une augmentation correspondante de la longueur de chaîne qui doit être déplacé afin de déplacer la charge. Ces effets résultent finalement en tandem dans la conservation de l'énergie mécanique depuis le travail effectué sur la charge est la même, peu importe la complexité de la machine.
Force élastique

Une force élastique agit pour retourner un ressort dans sa longueur naturelle. Une printemps idéal est considérée comme sans masse, sans frottement, incassable, et infiniment extensible. Ces ressorts exercent des forces qui poussent lorsqu'elles sont contractées, ou tirer lorsqu'il est étendu, en proportion du déplacement du ressort de sa position d'équilibre. Cette relation linéaire a été décrite par Robert Hooke en 1676, pour qui . La loi de Hooke est nommé Si  est le déplacement, la force exercée par un ressort idéal est égal à:
est le déplacement, la force exercée par un ressort idéal est égal à:
où  est la constante de ressort (ou constante de force), qui est notamment à la source. Représente le signe moins de la tendance de la force élastique d'agir en opposition à la charge appliquée.
est la constante de ressort (ou constante de force), qui est notamment à la source. Représente le signe moins de la tendance de la force élastique d'agir en opposition à la charge appliquée.
Force centripète
Pour un objet d'accélération dans le mouvement circulaire, la force déséquilibré agissant sur l'objet est égal à
où  est la masse de l'objet,
est la masse de l'objet, 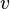 est la vitesse de l'objet et
est la vitesse de l'objet et  est la distance à l'axe de la trajectoire circulaire et
est la distance à l'axe de la trajectoire circulaire et 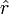 est le pointant unité de vecteur dans la direction radiale vers l'extérieur à partir du centre. Cela signifie que la force centripète déséquilibré ressentie par un objet est toujours dirigée vers le centre de la trajectoire de bombage. Ces forces agissent perpendiculairement au vecteur vitesse associé au mouvement d'un objet, et par conséquent ne modifient pas la vitesse de l'objet (grandeur de la vitesse), mais seulement dans la direction du vecteur vitesse. La force non équilibrée qui permet d'accélérer un objet peut être décomposée en une composante qui est perpendiculaire à la trajectoire, et qui est tangent à la trajectoire. Cela donne à la fois la force tangentielle qui accélère l'objet soit par le ralentir ou l'accélérer et la force radiale (centripète) qui change sa direction.
est le pointant unité de vecteur dans la direction radiale vers l'extérieur à partir du centre. Cela signifie que la force centripète déséquilibré ressentie par un objet est toujours dirigée vers le centre de la trajectoire de bombage. Ces forces agissent perpendiculairement au vecteur vitesse associé au mouvement d'un objet, et par conséquent ne modifient pas la vitesse de l'objet (grandeur de la vitesse), mais seulement dans la direction du vecteur vitesse. La force non équilibrée qui permet d'accélérer un objet peut être décomposée en une composante qui est perpendiculaire à la trajectoire, et qui est tangent à la trajectoire. Cela donne à la fois la force tangentielle qui accélère l'objet soit par le ralentir ou l'accélérer et la force radiale (centripète) qui change sa direction.
Forces fictives
Il existe des forces qui sont dépendants cadre, ce qui signifie qu'ils apparaissent en raison de l'adoption de la non-newtonienne (à savoir, non-inertielle) trames de référence. Ces forces comprennent la force centrifuge et la force de Coriolis. Ces forces sont considérées comme fictive parce qu'ils ne existent pas dans les cadres de référence qui ne sont pas d'accélération. Dans la relativité générale , la gravité devient une force d'inertie qui se pose dans les situations où l'espace-temps écarte d'une géométrie plane. Dans le prolongement, de Kaluza-Klein théorie et la théorie des cordes attribuent l'électromagnétisme et les autres forces fondamentales respectivement à la courbure de dimensions différemment-échelle, qui serait finalement implique que toutes les forces sont fictifs.
Rotations et couple
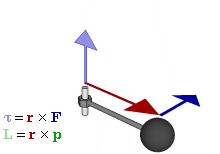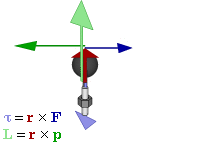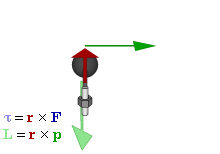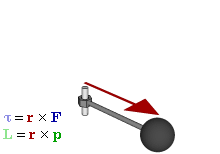
Forces qui causent des objets étendus à tourner sont associés à des couples. Mathématiquement, le couple sur une particule est défini comme le produit vectoriel :
où
 est de la particulevecteur de position de rapport à unpivot
est de la particulevecteur de position de rapport à unpivot est la force agissant sur la particule.
est la force agissant sur la particule.
Le couple est l'équivalent de la rotation de la force de la même manière que l'angle est l'équivalent de rotation pour la position, la vitesse angulaire de la vitesse , et le moment angulaire de l'élan . Tous les traitements formels des lois de Newton qui ont demandé aux forces appliquent de façon équivalente à des couples. Ainsi, comme une conséquence de la première loi du mouvement de Newton, il existe inertie de rotation qui assure que tous les organismes maintiennent leur moment angulaire à moins sollicité par un couple déséquilibré. De même, la deuxième loi du mouvement de Newton peut être utilisé pour dériver une autre définition du couple:
où
 est le moment d'inertie de la particule
est le moment d'inertie de la particule est l'accélération angulaire de la particule.
est l'accélération angulaire de la particule.
Ceci fournit une définition pour le moment d'inertie qui est l'équivalent de rotation pour la masse . Dans les traitements les plus avancés de la mécanique, le moment d'inertie agit comme un tenseur qui, lorsqu'il est correctement analysée, détermine entièrement les caractéristiques de rotations y compris précession et nutation.
De manière équivalente, la forme différentielle de la deuxième loi de Newton fournit une autre définition du couple:
où  est le moment cinétique de la particule.
est le moment cinétique de la particule.
La troisième loi de Newton sur le mouvement exige que tous les objets eux-mêmes l'expérience de couples exerçant des couples égaux et opposés, et donc implique aussi directement de laconservation du moment angulairepour les systèmes fermés qui connaissent les rotations et lesrévolutionsà travers l'action de couples internes.
Intégrales cinématiques
Les forces peuvent être utilisées pour définir un certain nombre de concepts physiques en intégrant par rapport à des variables cinématiques . Par exemple, en intégrant par rapport au temps donne la définition d' impulsion:
qui, par la deuxième loi de Newton, doit être équivalente à la variation de l'élan (donnant l'élan théorème Impulse).
De même, l'intégration par rapport à la position donne une définition pour letravail effectuépar une force:
qui, dans un système où toutes les forces sont prudentes ( voir ci-dessous ) est équivalent à des changements de cinétique et potentielle de l'énergie (rendement du théorème de l'énergie de travail ). La dérivée de la définition du travail donne une définition pour pouvoir en terme de force et de la vitesse (  ):
):
Énergie potentielle
Au lieu d'une force, le concept mathématiquement équivalent d'un champ d'énergie potentielle peut être utilisé pour plus de commodité. Par exemple, la force de gravitation agissant sur un corps peut être considéré comme l'action du champ de gravitation qui est présent à l'emplacement de l'organisme. Réaffirmant mathématiquement la définition de l'énergie (via définition de travail ), un potentiel champ scalaire 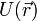 est défini comme ce domaine dont la pente est égale et opposée à la force produite sur tous les points:
est défini comme ce domaine dont la pente est égale et opposée à la force produite sur tous les points:
Forces peuvent être classés comme conservatrice ou non conservatrice. Les forces conservatrices sont équivalentes au gradient d'un potentiel tandis que les forces non conservatives ne sont pas.
Les forces conservatrices
A force conservatrice qui agit sur un système fermé a un travail mécanique associée qui permet l'énergie pour convertir seulement entre cinétiques ou formes potentielles. Cela signifie que pour un système fermé, le filet de l'énergie mécanique est conservée chaque fois qu'une force conservatrice agit sur le système. La force, par conséquent, est directement liée à la différence d'énergie potentielle entre deux endroits différents dans l'espace, et peut être considéré comme un artefact du champ potentiel de la même façon que la direction et la quantité d'un courant d'eau peuvent être considérées être un artefact de la carte de contour de l'élévation d'une zone.
Les forces conservatrices comprennent la gravité , l' électromagnétique vigueur, et de la force du ressort. Chacun de ces forces ont des modèles qui dépendent d'une position souvent donné comme un vecteur radial  émanant des potentiels à symétrie sphérique. Des exemples de ce suivi:
émanant des potentiels à symétrie sphérique. Des exemples de ce suivi:
Pour gravité:
où 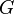 est le constante de gravitation, et
est le constante de gravitation, et est la masse de l'objetn.
est la masse de l'objetn.
Pour les forces électrostatiques:
où 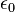 est permittivité électrique de l'espace libre, et
est permittivité électrique de l'espace libre, et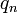 est lacharge électriquede l'objetn.
est lacharge électriquede l'objetn.
Pour les forces de printemps:
où  est le constante de ressort.
est le constante de ressort.
Forces non conservatives
Pour certains scénarios physiques, il est impossible de modéliser les forces comme étant dû à gradient de potentiel. Cela est souvent dû à des considérations macrophysiques que les forces de rendement comme résultant d'une moyenne statistique macroscopique de microétats. Par exemple, friction est causée par les gradients de nombreux potentiels électrostatiques entre les atomes , mais se manifeste comme un modèle de force qui est indépendant de tout vecteur de position échelle macroscopique. Forces non conservatives autres que la friction comprennent d'autres forces de contact, tension, la compression et la traînée. Toutefois, pour toute description suffisamment détaillée, toutes ces forces sont les résultats de ceux conservateur depuis chacune de ces forces macroscopiques sont les résultats nets des gradients de potentiels microscopiques.
La connexion entre les forces non-conservatrices macroscopiques et microscopiques forces conservatrices est décrit par un traitement détaillé avec la mécanique statistique . Dans les systèmes fermés macroscopiques, les forces non conservatives agissent pour changer les énergies internes du système, et sont souvent associées avec le transfert de la chaleur . Selon la deuxième loi de la thermodynamique , les forces non conservatives se traduisent nécessairement par des transformations d'énergie dans des systèmes fermés de l'ordre à des conditions plus aléatoires que l'entropie augmente.
Les unités de mesure
Le Unité SI de la force est le newton (symbole N), qui est la force nécessaire pour accélérer une masse d'un kilogramme à un taux de un mètre par seconde au carré, ou kg • m • s -2 . Le correspondant unité CGS est la dyne, la force nécessaire pour accélérer une masse d'un gramme par centimètre carré par seconde, ou g • cm • s -2 . 1 newton est donc égal à 100 000 dyne.
Le pieds-livre-deuxième unité impériale de la force est le livre-force (lbf), définie comme la force exercée par la gravité sur un livre-masse dans le champ gravitationnel niveau de 9,80665 m • s -2 . Le livre-force fournit une autre unité de la masse: un slug est la masse qui permettra d'accélérer par un pied carré par seconde lorsque agi par l'un livre-force. Une autre unité de la force dans le même système est le poundal, définie comme la force nécessaire pour accélérer une masse d'un livre à un taux d'un pied par seconde au carré. Les unités de limaces et poundal sont conçus pour éviter une constante de proportionnalité dans la deuxième loi de Newton .
Le livre-force a une contrepartie métrique, moins couramment utilisées que le newton: le kilogramme-force (kgf) (parfois kilopond), est la force exercée par la gravité standard sur un kilogramme de masse. Le kilogramme-force conduit à un autre, mais rarement unité de masse utilisée: la limace métrique (parfois de tasse ou hyl) est que la masse qui accélère à 1 m • s -2 lorsqu'elle est soumise à une force de 1 kgf. Le kilogramme-force ne fait pas partie de la modernité système de SI, et est généralement déconseillée; mais il voit encore utiliser à certaines fins comme exprimant la poussée, vélo tension des rayons, les paramètres de la clé dynamométrique et le couple de sortie du moteur. Autres unités arcanes de force comprennent l' sthène qui est équivalent à 1000 N et le kip, qui est équivalent à 1000 lbf.
| newton ( Unité SI) | dyne | kilogramme-force, kilopond | livre-force | poundal | |
|---|---|---|---|---|---|
| N 1 | ≡ 1 kg · m / s² | = 105dyn | ≈ 0,10197 kp | ≈ 0,22481lbF | ≈ 7,2330 pdl |
| 1 dyn | = 10-5N | ≡ 1 g · cm / s² | ≈ 1,0197 × 10-6kp | ≈ 2,2481 × 10-6 lbF | ≈ 7,2330 × 10-5PDL |
| 1 kp | = 9,80665 N | = 980665 dyn | ≡gn· (1 kg) | ≈ 2,2046lbF | ≈ 70,932 pdl |
| 1lbF | ≈ 4.448222 N | ≈ 444 822 dyn | ≈ 0,45359 kp | ≡gn· (1 kg) | ≈ 32,174 pdl |
| 1 pdl | ≈ 0.138255 N | ≈ 13825 dyn | ≈ 0.014098 kp | ≈ 0.031081lbF | ≡ £ 1 ·pi / s² |
| La valeur de gntel qu'il est utilisé dans la définition officielle du kilogramme-force est utilisée ici pour toutes les unités gravitationnelles. | |||||