
Régression linéaire
À propos de ce écoles sélection Wikipedia
SOS Enfants, un organisme de bienfaisance de l'éducation , a organisé cette sélection. Une bonne façon d'aider d'autres enfants est de parrainer un enfant
Régression linéaire est une forme d' analyse de régression dans lequel les données d'observation sont modélisés par un des moindres carrés fonction qui est un combinaison linéaire des paramètres du modèle et dépend d'un ou plusieurs variables indépendantes. Dans la régression linéaire simple la fonction de modèle représente une ligne droite. Les résultats de l'ajustement des données sont soumises à une analyse statistique.
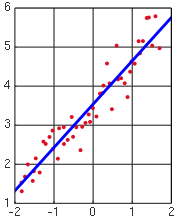
Définitions
Les données sont des valeurs de m  pris à partir d'observations de la variable dépendante ( variable de réponse)
pris à partir d'observations de la variable dépendante ( variable de réponse)  . La variable dépendante est sujette à l'erreur. Cette erreur est supposée être variable aléatoire , avec une moyenne de zéro. L'erreur systématique (par exemple signifie ≠ 0) peut être présent, mais son traitement est en dehors de la portée de l'analyse de régression. La variable indépendante ( variable explicative)
. La variable dépendante est sujette à l'erreur. Cette erreur est supposée être variable aléatoire , avec une moyenne de zéro. L'erreur systématique (par exemple signifie ≠ 0) peut être présent, mais son traitement est en dehors de la portée de l'analyse de régression. La variable indépendante ( variable explicative) 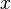 , Est sans erreur. Si ce ne est pas le cas, la modélisation devrait être fait en utilisant erreurs dans les variables de techniques de modèle. Les variables indépendantes sont également appelées variables explicatives, les variables exogènes, les variables d'entrée et des variables prédictives. Dans la régression linéaire simple du modèle de données est écrit comme
, Est sans erreur. Si ce ne est pas le cas, la modélisation devrait être fait en utilisant erreurs dans les variables de techniques de modèle. Les variables indépendantes sont également appelées variables explicatives, les variables exogènes, les variables d'entrée et des variables prédictives. Dans la régression linéaire simple du modèle de données est écrit comme
où  est une erreur d'observation.
est une erreur d'observation. 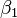 (Interception) et
(Interception) et  (Pente) sont les paramètres du modèle. En général, il ya n paramètres,
(Pente) sont les paramètres du modèle. En général, il ya n paramètres,  et le modèle peut se écrire
et le modèle peut se écrire
où les coefficients  sont des constantes ou des fonctions de la variable indépendante, x. Les modèles qui ne sont pas conformes à cette spécification doivent être traités par régression non linéaire.
sont des constantes ou des fonctions de la variable indépendante, x. Les modèles qui ne sont pas conformes à cette spécification doivent être traités par régression non linéaire.
Sauf indication contraire, on suppose que les erreurs d'observation sont décorrélées et appartiennent à une distribution normale . Ce, ou une autre hypothèse, est utilisé lors de l'exécution des tests statistiques sur les résultats de la régression. Une formulation équivalente de régression linéaire simple qui montre explicitement la régression linéaire comme un modèle de l'espérance conditionnelle peut être donnée quant
Le distribution conditionnelle de y x donnée est une transformation linéaire de la distribution du terme d'erreur.
Notation et conventions de nommage
- Scalaires et vecteurs sont désignés par des lettres minuscules.
- Matrices sont désignés par des lettres majuscules.
- Les paramètres sont désignées par des lettres grecques.
- Vecteurs et les matrices sont désignés par des lettres en gras.
- Un paramètre avec un chapeau, comme
 , Désigne un estimateur de paramètre.
, Désigne un estimateur de paramètre.
L'analyse des moindres carrés
Le premier objectif de l'analyse de régression est de mieux adapter les données en ajustant les paramètres du modèle. Parmi les différents critères qui peuvent être utilisés pour définir ce qui constitue un meilleur ajustement, le critère des moindres carrés est très puissant. La fonction objectif, S, est défini comme la somme des carrés des résidus, r i
où chaque résiduelle est la différence entre la valeur observée et la valeur calculée par le modèle:
Le meilleur ajustement est obtenu lorsque S, la somme des carrés des résidus, est minimisée. Sous réserve de certaines conditions, les paramètres ont ensuite minimum variance ( Théorème de Gauss-Markov) et peuvent aussi représenter un solution du maximum de vraisemblance pour le problème d'optimisation.
De la théorie de linéaires des moindres carrés, les estimateurs de paramètres sont trouvées en résolvant les équations normales
En notation matricielle, ces équations sont écrites en tant que
 ,
,
Et ce est ainsi lorsque la matrice  est non singulière:
est non singulière:
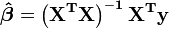 ,
,
Plus précisément, pour le montage linéaire, cela est indiqué dans raccord de ligne droite.
les statistiques de régression
Le deuxième objectif de régression est l'analyse statistique des résultats de l'ajustement des données.
Notons  la variance du terme d'erreur
la variance du terme d'erreur  (De sorte que
(De sorte que 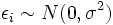 pour chaque
pour chaque  ). Une estimation non biaisée de
). Une estimation non biaisée de  est donnée par
est donnée par
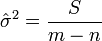 .
.
La relation entre l'estimation et la valeur réelle est:
où  a la distribution chi carré avec
a la distribution chi carré avec 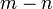 degrés de liberté.
degrés de liberté.
L'application de ce critère exige que  , La variance d'une observation de poids unitaire, être estimée. Si le
, La variance d'une observation de poids unitaire, être estimée. Si le 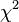 Le test est passé, les données peuvent être dit à être monté à l'intérieur erreur d'observation.
Le test est passé, les données peuvent être dit à être monté à l'intérieur erreur d'observation.
La solution des équations normales peut se écrire
Cela montre que les estimateurs de paramètres sont des combinaisons linéaires de la variable dépendante. Il se ensuit que, si les erreurs d'observation sont normalement distribuées, les estimateurs de paramètres seront appartenir à un la distribution t de Student avec 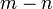 degrés de liberté. L' écart-type sur un estimateur de paramètres est donnée par
degrés de liberté. L' écart-type sur un estimateur de paramètres est donnée par
Le  intervalle de confiance pour le paramètre,
intervalle de confiance pour le paramètre, 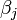 , Est calculée comme suit:
, Est calculée comme suit:
Les résidus peuvent être exprimées comme
La matrice  qui est connu comme le matrice chapeau et a la propriété utile qui il est idempotent. En utilisant cette propriété, il peut être démontré que, si les erreurs sont normalement distribuées, les résidus suivront un la distribution t de Student avec
qui est connu comme le matrice chapeau et a la propriété utile qui il est idempotent. En utilisant cette propriété, il peut être démontré que, si les erreurs sont normalement distribuées, les résidus suivront un la distribution t de Student avec 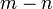 degrés de liberté. Studentisés résidus sont utiles dans les tests pour aberrantes.
degrés de liberté. Studentisés résidus sont utiles dans les tests pour aberrantes.
Compte tenu de la valeur de la variable indépendante, x d, la réponse prédite est calculée comme
Écrit les éléments 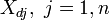 comme
comme  , Le
, Le  intervalle de confiance de réponse signifie pour la prédiction est donnée, en utilisant théorie de la propagation de l'erreur, par:
intervalle de confiance de réponse signifie pour la prédiction est donnée, en utilisant théorie de la propagation de l'erreur, par:
Le  les intervalles de confiance de réponse prédites pour les données sont données par:
les intervalles de confiance de réponse prédites pour les données sont données par:
 .
.
Cas linéaire
Dans le cas où la formule à équiper est une ligne droite,  Les équations normales sont
Les équations normales sont
où toutes les sommations sont de i = 1 à i = m. De là, par La règle de Cramer,
où
La matrice de covariance est
Le signifie intervalle de confiance de réponse est donnée par
Le prévoir un intervalle de confiance de la réponse est donnée par
Analyse des écarts
L'analyse de variance est similaire à ANOVA en ce que la somme des carrés des résidus se décompose en deux composantes. La somme des carrés de régression (ou la somme des carrés des résidus) SSR (aussi communément appelé RSS) est donné par:
où 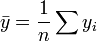 et u est un n par une unité vecteur (ce est à dire chaque élément est 1). Notez que les termes
et u est un n par une unité vecteur (ce est à dire chaque élément est 1). Notez que les termes  et
et  sont tous deux équivalents à
sont tous deux équivalents à 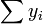 , Et ainsi le terme
, Et ainsi le terme 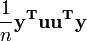 est équivalent à
est équivalent à 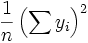 .
.
L'erreur (ou inexpliquée) somme des carrés ESS est donné par:
La somme totale des carrés est donnée par TSS
Le coefficient de Pearson de la régression, R ² est alors donnée comme
Exemple
Pour illustrer les différents objectifs de la régression, nous donnons un exemple. L'ensemble de données suivant donne les hauteurs moyennes et les poids pour les femmes américaines de 30 à 39 (source: Le World Almanac and Book des faits, 1975) âgés.
Hauteur / m 1,47 1,5 1,52 1,55 1,57 1,60 1,63 1,65 1,68 1,7 1,73 1,75 1,78 1,8 1,83 Poids / kg 52,21 53,12 54,48 55,84 57,2 58,57 59,93 61,29 63,11 64,47 66,28 68,1 69,92 72,19 74,46
Une parcelle de poids contre la hauteur (voir ci-dessous) montre qu'il ne peut pas être modélisée par une ligne droite, donc une régression est effectuée en modélisant les données par une parabole.
où la variable dépendante, y, est le poids et la variable indépendante, x est la hauteur.
Placez les coefficients,  , Des paramètres de la i ème ème observation dans la ligne i de la matrice X.
, Des paramètres de la i ème ème observation dans la ligne i de la matrice X.

Les valeurs des paramètres sont trouvées en résolvant les équations normales
Élément ij de la matrice de l'équation normale, 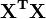 est formé en additionnant les produits de la colonne i et la colonne j de X.
est formé en additionnant les produits de la colonne i et la colonne j de X.
Élément i du vecteur de droite  est formé en additionnant les produits de la colonne i de X avec la colonne de valeurs de variables indépendantes.
est formé en additionnant les produits de la colonne i de X avec la colonne de valeurs de variables indépendantes.
Ainsi, les équations normales sont
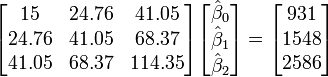
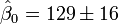 (Valeur
(Valeur 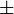 écart-type)
écart-type) 
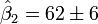
Les valeurs calculées sont donnés par
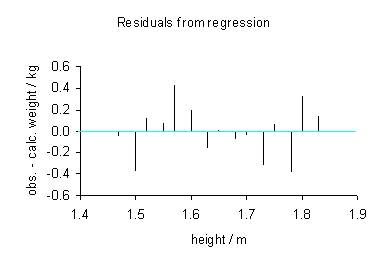
Les données observées et calculées sont tracées ensemble et les résidus,  , Sont calculés et tracés. Les écarts-types sont calculés en utilisant la somme des carrés,
, Sont calculés et tracés. Les écarts-types sont calculés en utilisant la somme des carrés, 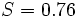 .
.
Les intervalles de confiance sont calculés en utilisant:
avec  = 5%,
= 5%,  = 2,2. Par conséquent, nous pouvons dire que les 95% intervalles de confiance sont:
= 2,2. Par conséquent, nous pouvons dire que les 95% intervalles de confiance sont:
Vérifier les hypothèses du modèle
Les hypothèses du modèle sont vérifiées par calcul des résidus et de les tracer. Les parcelles suivantes peuvent être construits pour tester la validité des hypothèses:
- Résidus contre la variable explicative, comme illustré ci-dessus.
- Un temps de terrain série de résidus, ce est-à tracer les résidus en tant que fonction du temps.
- Résidus contre les valeurs ajustées,
 .
. - Les résidus résiduelle contre le précédent.
- Un tracé de probabilité normale des résidus de tester la normalité. Les points doivent se situer le long d'une ligne droite.
Il ne devrait pas y avoir de motif sensible aux données de tous, mais la dernière parcelle
Vérification de la validité du modèle
La validité du modèle peut être vérifiée en utilisant l'une des méthodes suivantes:
- Utilisation de l'intervalle de confiance pour chacun des paramètres,
 . Si l'intervalle de confiance comprend 0, le paramètre peut être retiré à partir du modèle. Idéalement, une nouvelle analyse de régression excluant ce paramètre serait nécessaire d'effectuer et a continué jusqu'à ce qu'il n'y a plus de paramètres à supprimer.
. Si l'intervalle de confiance comprend 0, le paramètre peut être retiré à partir du modèle. Idéalement, une nouvelle analyse de régression excluant ce paramètre serait nécessaire d'effectuer et a continué jusqu'à ce qu'il n'y a plus de paramètres à supprimer. - Lors du montage d'une ligne droite, calculer le coefficient de Pearson de régression. Plus la valeur est de 1; meilleure est la régression est. Ce coefficient donne ce fraction du comportement observé peut être expliqué par les variables données.
- Examiner les intervalles de confiance d'observation et de prévision. Plus elles sont le mieux.
- Le calcul de la F-statistiques.
D'autres procédures
Pondérées moindres carrés
Pondérées moindres carrés est une généralisation de la méthode des moindres carrés, utilisée lorsque les erreurs d'observation ont une variance inégale.
Modèle erreurs dans les variables
Modèle erreurs dans les variables ou les moindres carrés totale lorsque la variable indépendante est sujette à l'erreur
Modèle linéaire généralisé
Modèle linéaire généralisé est utilisé lorsque la fonction de distribution des erreurs ne est pas une distribution normale. Les exemples incluent la distribution exponentielle , la distribution gamma, La distribution gaussien inverse, distribution de Poisson , loi binomiale , distribution multinomiale
Régression robuste
Une foule d'autres approches pour le calcul des paramètres de régression sont inclus dans la catégorie dite régression robuste. Une technique minimise la moyenne erreur absolue, ou une autre fonction des résidus, au lieu de l'erreur quadratique moyenne comme dans la régression linéaire. Régression robuste est beaucoup plus de calculs que la régression linéaire et est un peu plus difficile à mettre en œuvre ainsi. Bien que les estimations des moindres carrés ne sont pas très sensibles à la rupture de la normalité de l'hypothèse des erreurs, ce ne est pas vrai quand la variance ou moyenne de la distribution d'erreur ne est pas borné, ou quand un analyste qui permet d'identifier les valeurs aberrantes ne est pas disponible.
Entre Utilisateurs Stata, la régression robuste est souvent pris pour signifier régression linéaire avec les estimations de l'erreur type de Huber-White en raison des conventions de nommage pour les commandes de régression. Cette procédure assouplit l'hypothèse de homoscédasticité estimations de la variance pour seulement; les prédicteurs sont encore moindres carrés ordinaires (MCO) des estimations. Cela conduit parfois à la confusion; Stata utilisateurs croient parfois que la régression linéaire est une méthode robuste lorsque cette option est utilisée, même si elle ne est pas réellement robuste dans le sens de la valeur aberrante résistance.
Applications de régression linéaire
Régression linéaire est largement utilisé dans les sciences biologiques, comportementales et sociales pour décrire les relations entre les variables. Il est classé comme l'un des outils les plus importants utilisés dans ces disciplines.
La ligne de tendance
Une ligne de tendance représente une tendance, le mouvement à long terme des données de séries chronologiques après d'autres composants ont été comptabilisées. Il indique si un ensemble de données particulier (disons PIB, des prix du pétrole ou des prix d'achat d'actions) ont augmenté ou diminué au cours de la période de temps. Une ligne de tendance pourrait être simplement dessinée par œil à travers un ensemble de points de données, mais plus correctement leur position et la pente est calculée en utilisant des techniques statistiques comme la régression linéaire. Les lignes de tendance sont généralement des lignes droites, bien que certaines variations utilisent des polynômes de degré plus élevé selon le degré de courbure désirée dans la ligne.
Les lignes de tendance sont parfois utilisés en analyse d'affaires pour montrer les changements dans les données au fil du temps. Ceci a l'avantage d'être simple. Les lignes de tendance sont souvent utilisés pour faire valoir qu'une action particulière ou un événement (comme la formation, ou une campagne de publicité) ont causé les changements observés à un moment donné. Ce est une technique simple, et ne nécessite pas un groupe de contrôle, la conception expérimentale, ou une technique d'analyse sophistiqués. Cependant, il souffre d'un manque de validité scientifique dans les cas où d'autres changements potentiels peuvent affecter les données.
Médecine
À titre d'exemple, des signes précoces concernant le tabagisme à la mortalité et la morbidité provenaient d'études employant régression. Les chercheurs comprennent généralement plusieurs variables dans leur analyse de régression dans un effort pour éliminer les facteurs qui pourraient produire corrélations parasites. Pour l'exemple de la cigarette, les chercheurs pourraient inclure le statut socio-économique, en plus de fumer pour se assurer que tout effet du tabagisme sur la mortalité observée ne est pas due à un effet de l'éducation ou de revenu. Cependant, il ne est jamais possible d'inclure toutes les variables de confusion possibles dans une étude utilisant la régression. Pour l'exemple de fumer, un gène hypothétique pourrait augmenter la mortalité et aussi inciter les gens à fumer davantage. Pour cette raison, essais contrôlés randomisés sont considérés comme plus fiables que d'une analyse de régression.
Financement
Le modèle capital asset pricing utilise régression linéaire ainsi que le concept de Beta pour analyser et quantifier le risque systématique d'un investissement. Cela vient directement du Coefficient bêta du modèle de régression linéaire qui concerne le retour sur l'investissement pour le retour sur tous les actifs risqués.
Régression peut ne pas être le moyen approprié pour estimer beta dans la finance étant donné qu'il est censé fournir la volatilité d'un investissement par rapport à la volatilité du marché dans son ensemble. Il faudrait pour cela que ces deux variables sont traités de la même façon lors de l'estimation de la pente. Considérant que la traite régression tous comme étant la variabilité dans l'investissement des rendements variables, à savoir qu'il ne considère résidus dans la variable dépendante.
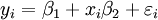
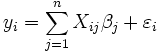
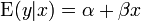
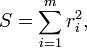
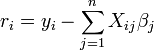

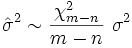

![\ Hat \ sigma_j = \ sqrt {\ frac {S} {mn} \ left [\ mathbf {(X ^ TX)} ^ {- 1} \ right] _ {}} jj](../../images/216/21697.png)



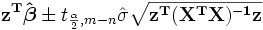




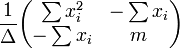
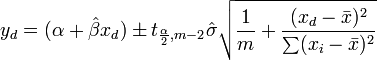

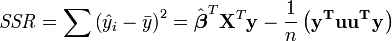
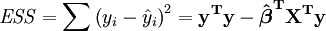
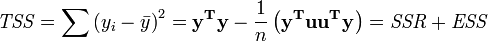


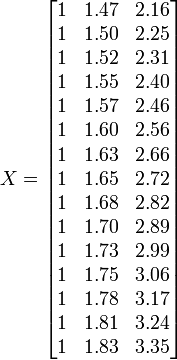

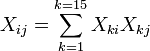


![[\ Hat {\ beta_j} - \ sigma_j t_ {mn; 1- \ frac {\ alpha} {2}}; \ hat {\ beta_j} + \ sigma_j t_ {mn; 1- \ frac {\ alpha} {2 }}]](../../images/217/21747.png)
![\ Beta_0 \ in [92.9,164.7]](../../images/217/21749.png)
![\ Beta_1 \ in [-186,8, -99,5]](../../images/217/21750.png)
![\ Beta_2 \ in [48.7,75.2]](../../images/217/21751.png)
