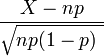Distribution binomiale
Saviez-vous ...
Ce contenu de Wikipedia a été sélectionné par SOS Enfants d'aptitude dans les écoles à travers le monde. Une bonne façon d'aider d'autres enfants est de parrainer un enfant
Fonction de masse 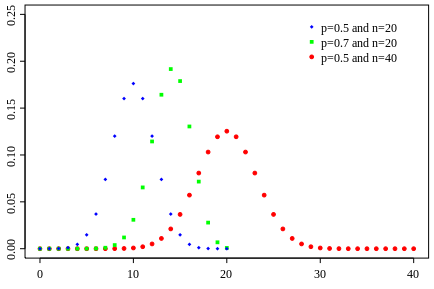 | |
Fonction de distribution cumulative 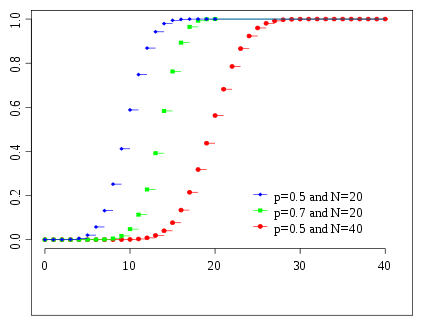 Couleurs correspondent à l'image ci-dessus | |
| Paramètres |  nombre d'essais ( entier ) nombre d'essais ( entier )  probabilité de succès ( réel ) probabilité de succès ( réel ) |
|---|---|
| Soutien |  |
| PMF | 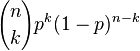 |
| CDF |  |
| Signifier |  |
| Médiane | un des  |
| Mode | 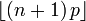 |
| Variance | 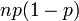 |
| Asymétrie | 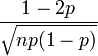 |
| Ex. aplatissement |  |
| Entropy |  |
| MGF |  |
| FC | 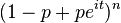 |
Dans la théorie des probabilités et des statistiques , la distribution binomiale est la distribution de probabilité discrète du nombre de succès dans une séquence de n oui / non expériences indépendantes, dont chacune rendements succès avec probabilité p. Une telle / expérience de l'échec de réussite est aussi appelé une expérience de Bernoulli ou Essai de Bernoulli. En fait, lorsque n = 1, la distribution binomiale est un Distribution de Bernoulli. La distribution binomiale est la base de la populaire test binomial de signification statistique. Une distribution binomiale ne doit pas être confondu avec un distribution bimodale.
Exemples
Un exemple élémentaire est la suivante: Passer une norme mourir dix fois et compter le nombre de six. La distribution de ce nombre aléatoire est une distribution binomiale avec n = 10 et p = 1/6.
Comme autre exemple, supposons 5% d'une très grande population d'être aux yeux verts. Vous choisissez 100 personnes au hasard. Le nombre de personnes aux yeux verts que vous choisissez est une variable aléatoire X qui suit une loi binomiale avec n = 100 et p = 0,05.
Spécification
Fonction de masse
En général, si la variable aléatoire K suit la loi binomiale de paramètres n et p, nous écrivons K ~ B (n, p). La probabilité d'obtenir exactement k succès dans les essais n est donnée par la probabilité fonction de masse:
pour k = 0, 1, 2, ..., n et où
est le coefficient binomial (d'où le nom de la distribution) "n choisir k" (également notée C (n, k) ou n C k). La formule peut être comprise comme suit: nous voulons k succès (p k) et n - k échecs (1 - p) n - k. Toutefois, les succès k peuvent se produire ne importe où entre les n essais, et il n'y a C (n, k) différentes façons de distribuer k succès dans une séquence de n essais.
Dans la création de tables de référence pour probabilité de distribution binomiale, habituellement le tableau est rempli jusqu'à n / 2 valeurs. En effet, pour k> n / 2, la probabilité peut être calculée en tant que son complément
Donc, il faut regarder à un k différent et une autre p (le binôme ne est pas symétrique en général).
Fonction de distribution cumulative
Le fonction de distribution cumulative peut être exprimée en termes de la régularisé fonction bêta incomplète, comme suit:
à condition que k est un entier et 0 ≤ k ≤ n. Si x ne est pas nécessairement un nombre entier ou pas nécessairement positif, on peut se exprimer ainsi:
Pour k ≤ np, les limites supérieures de la queue inférieure de la fonction de distribution peuvent être dérivées. En particulier, Inégalité de Hoeffding donne la borne
et Inégalité de Chernoff peut être utilisée pour dériver la limite
Moyenne, la variance et le mode
Si X ~ B (n, p) (ce est-à X est une variable aléatoire binomiale distribué), le valeur attendue de X est
et la variance est
Ce fait est facilement prouvé comme suit. Supposons d'abord que nous avons exactement un essai de Bernoulli. Nous avons deux résultats possibles, 1 et 0, le premier ayant probabilité p et la seconde ayant une probabilité - p; la moyenne pour cet essai est donnée par μ = p. En utilisant la définition de la variance , on a
Maintenant supposons que nous voulons que la variance pour ces essais n (ce est à dire pour la loi binomiale général). Depuis les essais sont indépendants, on peut ajouter les écarts pour chaque essai, donnant
Le Mode de X est le plus grand entier inférieur ou égal à (n + 1) p; si m = (n + 1) p est un nombre entier, alors m - 1 et m sont les deux modes.
Dérivations explicites de moyenne et la variance
Nous dérivons ces quantités à partir des premiers principes. Certaines sommes particuliers se produisent dans ces deux dérivations. Nous réorganisons les sommes et les conditions afin que résume uniquement sur les fonctions de masse de probabilité binomiale complets ( PMF ) se pose, qui sont toujours l'unité
Signifier
Nous appliquons la définition de la valeur attendue d'une variable aléatoire discrète à la distribution binomiale
Le premier terme de la série (d'indice k = 0) a la valeur 0 puisque le premier facteur, k, est nul. Il peut donc être écartée, ce est à dire que nous pouvons changer la limite inférieure à: k = 1
Nous avons tiré de facteurs n et k sur les factorielles, et une puissance de P a été scindé. Nous nous préparons à redéfinir les indices.
Nous renommer m = n - 1 et s = k - 1. La valeur de la somme ne est pas modifié par cela, mais il devient désormais facilement identifiables
La somme qui a suivi est une somme sur un binôme complète pmf (d'un ordre inférieur à la somme initiale, en l'occurrence). Ainsi
Variance
On peut montrer que la variance est égale à (voir: la variance, 10. formule de calcul de la variance ):
En utilisant cette formule, nous voyons que nous avons maintenant besoin de la valeur attendue de X 2, qui est
Nous pouvons utiliser notre expérience acquise ci-dessus en dérivant la moyenne. Nous savons comment traiter une facteur k. Cela nous arrive aussi loin que
(À nouveau, avec m = n - 1 et s = k - 1). Nous avons divisé la somme en deux sommes séparés et nous reconnaissons chacun
La première somme est identique dans la forme à celle nous avons calculé dans la moyenne (ci-dessus). Il résume à point de fusion. La deuxième somme est l'unité.
En utilisant ce résultat dans l'expression de la variance, avec le moyen (E (X) = np), nous obtenons
Relations avec d'autres distributions
Sommes des binômes
Si X ~ B (n, p) et Y ~ B (m, p) sont des variables binomiales indépendantes, alors x + y est de nouveau une variable binomiale; sa distribution est
Approximation normale

Si n est suffisamment grand, la dissymétrie de la distribution ne est pas trop grande, et une approprié correction de continuité est utilisé, une excellente approximation à B (n, p) est donnée par la distribution normale
Divers règles empiriques peuvent être utilisés pour décider si n est assez grand. Une règle est que les deux np et n (1 - p) doit être supérieur à 5. Toutefois, le nombre précis varie d'une source à, et dépend de comment bon une approximation on veut; certaines sources donnent 10. Une autre règle couramment utilisé soutient que l'approximation normale ci-dessus est appropriée que si
Ce qui suit est un exemple de l'application d'un correction de continuité: Supposons que l'on souhaite calculer Pr (X ≤ 8) pour un binôme variable aléatoire X. Si Y a une distribution donnée par l'approximation normale, puis Pr (X ≤ 8) est approchée par le Pr (Y ≤ 8,5). L'addition de 0,5 est la correction de continuité; l'approximation normale non corrigée donne des résultats beaucoup moins précises.
Cette approximation est un gain de temps énorme (des calculs exacts avec grande n sont très onéreux); Historiquement, ce est la première utilisation de la distribution normale, introduit en Le livre d'Abraham de Moivre La théorie des probabilités en 1733. Aujourd'hui, elle peut être considérée comme une conséquence de la théorème central limite puisque B (n, p) est une somme de n indépendant, identiquement distribuées 0-1 variables indicatrices.
Par exemple, supposons que vous goûter au hasard n personnes sur une population nombreuse et leur demander se ils sont d'accord avec un certain déclaration. La proportion de personnes qui acceptent dépendra bien sûr sur l'échantillon. Si vous avez échantillonné groupes de n personnes à plusieurs reprises et véritablement au hasard, les proportions souhaitez suivre une distribution normale avec une moyenne approximative égale à la proportion vraie p d'accord dans la population et avec un écart type σ = (p (1 - p) n) 1 / 2. Grand taille de l'échantillon n sont bonnes parce que l'écart-type, en proportion de la valeur attendue, devient plus petit, ce qui permet une estimation plus précise du paramètre inconnu p.
Approximation de Poisson
La distribution binomiale converge vers la distribution de Poisson comme le nombre d'essais tend vers l'infini tandis que le produit np reste fixe. Par conséquent, la loi de Poisson de paramètre λ = np peut être utilisée comme une approximation de B (n, p) de la distribution binomiale si n est suffisamment grand et p est suffisamment faible. Selon deux règles de base, cette approximation est bonne si n ≥ 20 et p ≤ 0,05, ou si n ≥ 100 et ≤ 10 np.
Limites de la distribution binomiale
- Comme n tend vers ∞ et p se approche de 0 alors np reste fixé à λ> 0 ou au moins np approche λ> 0, alors le binomiale (n, p) la distribution se rapproche de la distribution de Poisson avec λ de valeur attendue.
- Lorsque n tend vers ∞ p reste fixe alors que, la répartition des
- se rapproche de la distribution normale avec la valeur attendue 0 et variance 1 (ce est juste un cas spécifique de la Théorème central limite).



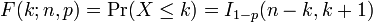

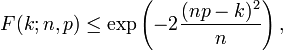

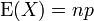
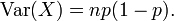
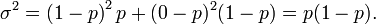



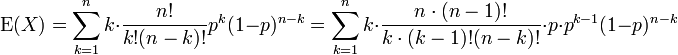
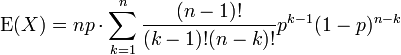


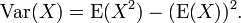

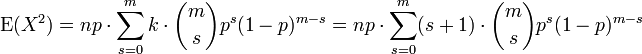



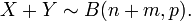
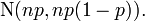
![\ Mu h \ 3 \ sigma = np \ h 3 \ sqrt {np (1-p)} \ in [0, n].](../../images/195/19591.png)