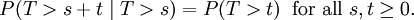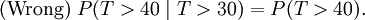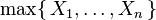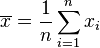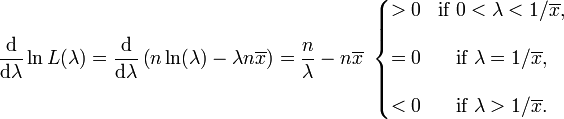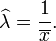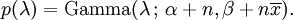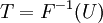Distribution exponentielle
Contexte des écoles Wikipédia
SOS Enfants, un organisme de bienfaisance de l'éducation , a organisé cette sélection. Avec enfants SOS vous pouvez choisir de parrainer des enfants dans plus de cent pays
Densité de probabilité  | |
Fonction de distribution cumulative 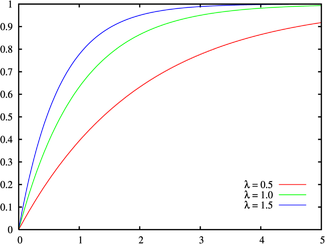 | |
| Paramètres | 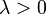 taux ou échelle inverse ( réel ) taux ou échelle inverse ( réel ) |
|---|---|
| Soutien |  |
 | |
| CDF | 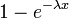 |
| Signifier |  |
| Médiane |  |
| Mode | 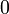 |
| Variance |  |
| Asymétrie | 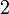 |
| Ex. aplatissement |  |
| Entropy |  |
| MGF |  |
| FC |  |
Dans la théorie des probabilités et des statistiques , les distributions exponentielles sont une classe de continues distributions de probabilité . Une distribution exponentielle se pose naturellement lors de la modélisation du temps entre les événements indépendants qui se produisent à un taux moyen constant.
Caractérisation
Densité de probabilité
Le fonction de densité de probabilité (pdf) d'une distribution exponentielle est de la forme
où λ> 0 est un paramètre de distribution, souvent appelé le paramètre de débit. La distribution est supporté sur l'intervalle [0, ∞). Si une variable aléatoire X a cette distribution, nous écrire X ~ exponentiel (λ).
Fonction de distribution cumulative
Le fonction de distribution cumulative est donnée par
Paramétrage suppléant
Une alternative paramétrage est couramment utilisé pour définir le fonction de densité de probabilité (pdf) d'une distribution exponentielle
où β> 0 est un paramètre d'échelle de la distribution et est le réciproque du paramètre de vitesse, λ, définis ci-dessus. Dans cette description, β est un paramètre de survie dans ce sens que si une variable aléatoire X est la durée de temps pendant laquelle un système biologique ou mécanique donnée M parvient à survivre et X ~ exponentielle (β), puis ![\ Mathbb {} E [X] = \ beta](../../images/77/7760.png) . Ce est-à-dire la durée prévue de la survie des unités M est β de temps.
. Ce est-à-dire la durée prévue de la survie des unités M est β de temps.
Cette spécification autre est parfois plus pratique que celle donnée ci-dessus, et certains auteurs se utiliser comme une définition standard. Nous ne assumons cette spécification autre. Malheureusement, cela donne lieu à un l'ambiguïté de notation. En général, le lecteur doit vérifier lequel de ces deux spécifications est utilisé si un auteur écrit "X ~ exponentiel (λ)", soit depuis la notation dans la précédente (en utilisant λ) ou la notation dans cette section (ici, en utilisant β pour éviter toute confusion) pourrait être prévu.
Présence et applications
La distribution exponentielle se produit naturellement dans la description de la longueur des temps inter-arrivées homogène dans un Processus de Poisson.
La distribution exponentielle peut être considéré comme un homologue continu de la distribution géométrique, qui décrit le nombre de Bernoulli nécessaires pour un processus discret changement d'état. En revanche, la distribution exponentielle décrit le temps pour un procédé en continu pour changer d'état.
Dans les scénarios du monde réel, l'hypothèse d'un taux constant (ou la probabilité par unité de temps) est rarement satisfait. Par exemple, le taux d'appels téléphoniques entrants est différente selon le moment de la journée. Mais si nous nous concentrons sur un intervalle de temps pendant laquelle le taux est à peu près constante, tels que 2-4 heures en jours de travail, la distribution exponentielle peut être utilisé comme un bon modèle approximatif pour le moment jusqu'à ce que le prochain appel téléphonique arrive. Réserves similaires se appliquent aux exemples suivants qui donnent les variables approximativement exponentielle distribués:
- le temps jusqu'à ce qu'une particule radioactive se désintègre, ou le temps entre les signaux sonores d'un compteur Geiger;
- le temps qu'il faut avant votre prochain appel téléphonique
- le temps jusqu'à ce défaut (sur le paiement aux détenteurs de la dette de l'entreprise) sous forme réduite modélisation du risque de crédit
Les variables exponentielles peuvent également être utilisés pour modéliser des situations où certains événements se produisent avec une probabilité constante par unité de distance:
- la distance entre mutations sur un ADN brin;
- la distance entre roadkill sur une rue donnée;
En la théorie des files, les temps entre les arrivées (c.-à-temps entre les clients entrent dans le système) sont souvent modélisés comme des variables réparties de façon exponentielle. La longueur d'un processus qui peut être considéré comme une séquence de plusieurs tâches indépendantes est mieux modélisée par une variable après la Distribution d'Erlang (qui est la distribution de la somme de plusieurs variables indépendantes réparties de façon exponentielle).
la théorie de la fiabilité et de ingénierie de la fiabilité également faire usage extensif de la distribution exponentielle. En raison de l' absence de mémoire propriété de cette distribution, il est bien adapté pour modéliser la constante partie de taux de risque de la courbe en baignoire utilisée dans la théorie de la fiabilité. Il est également très pratique car il est si facile d'ajouter les taux d'échec dans un modèle de fiabilité. La distribution exponentielle est cependant pas appropriée pour modéliser la durée de vie globale des organismes ou des dispositifs techniques, parce que les "taux d'échec" ici ne sont pas constantes: plus d'échecs se produisent pour les très jeunes et pour les très vieux systèmes.
Dans la physique , si vous observez un gaz à un prix fixe de température et pression dans un uniforme champ gravitationnel, les hauteurs des différentes molécules suivent également une distribution exponentielle approximative. Ceci est une conséquence de la propriété mentionnée ci-dessous entropique.
Propriétés
Moyenne et la variance
La moyenne ou valeur attendue d'une variable aléatoire X distribué de façon exponentielle avec le paramètre de taux λ est donnée par
À la lumière des exemples donnés ci-dessus, cela fait sens: si vous recevez des appels téléphoniques à un taux moyen de 2 par heure, alors vous pouvez vous attendre à attendre une demi-heure pour chaque appel.
La variance de X est donnée par
Perte de mémoire
Une propriété importante de la distribution exponentielle est qu'il est sans mémoire. Cela signifie que si une variable aléatoire T est distribué de façon exponentielle, de sa obéit probabilités conditionnelles
Ce dit que le probabilité conditionnelle que nous devons attendre, par exemple, plus de 10 secondes avant la première arrivée, étant donné que la première arrivée n'a pas encore passé après 30 secondes, ne est pas différent de la probabilité initiale que nous devons attendre plus de 10 secondes pour la première arrivée. Ce est souvent mal compris par les étudiants qui suivent des cours sur la probabilité: le fait que P (T> 40 | T> 30) = P (T> 10) ne signifie pas que les événements T> 40 et T> 30 sont indépendante. Pour résumer: "Perte de mémoire" de la distribution de probabilité du délai d'attente T jusqu'à ce que les premiers moyens d'arrivée
Cela ne signifie pas
(Ce serait l'indépendance. Ces deux événements ne sont pas indépendants.)
Les distributions exponentielles et la distributions géométriques sont les seules distributions de probabilité sans mémoire.
La distribution exponentielle a également une constante fonction de risque.
Quartiles
La fonction quantile (fonction de distribution cumulative inverse) pour exponentiel (λ) est
pour 0 ≤ p <1. Le quartiles sont donc:
- premier quartile
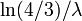
- médiane
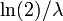
- troisième quartile
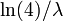
Kullback-Leibler
La scène Kullback-Leibler entre Exp (λ 0) («vraie» distribution) et Exp (λ) («rapprochant» distribution) est donnée par
Distribution d'entropie maximale
Parmi toutes les distributions de probabilités continues avec le soutien [0, ∞) et μ dire, la distribution exponentielle avec λ = 1 / μ a plus grand entropie.
Répartition du minimum de variables aléatoires exponentielles
Soit X 1, ..., X n soit variables aléatoires indépendantes distribuées de façon exponentielle avec des paramètres de taux λ 1, ..., λ n. Puis
est également une distribution exponentielle, avec le paramètre
Cependant,
ne est pas une distribution exponentielle.
Estimation des paramètres
Supposons que vous savez qu'une variable donnée est distribué de façon exponentielle et que vous voulez estimer le paramètre de taux λ.
Maximum de vraisemblance
Le fonction de vraisemblance pour λ, étant donné un échantillon indépendant et identiquement distribuées x = (x 1, ..., x n) tiré de votre variable, est
où
est la moyenne d'échantillon.
Le dérivé du logarithme de la fonction de vraisemblance est
En conséquence, la estimation du maximum de vraisemblance pour le paramètre de vitesse est
Inférence bayésienne
Le conjugué préalable pour la distribution exponentielle est la la distribution gamma (dont la distribution exponentielle est un cas particulier). Le paramétrage suivants du gamma pdf est utile:
Le distribution a posteriori p peut alors être exprimée en termes de la fonction de vraisemblance défini ci-dessus et un gamma avant:
Maintenant, la densité a posteriori p a été déterminés jusqu'à une constante de normalisation manquantes. Comme il a la forme d'un gamma pdf, ce qui peut facilement être rempli, et l'on obtient
Ici, les paramètres α peut être interprété comme le nombre d'observations antérieures, β et que la somme des observations antérieures.
Génération variables aléatoires exponentielles
Une méthode conceptuellement très simple pour générer exponentielle variables aléatoires sont basées sur le transformation inverse échantillonnage: Étant donné une variable aléatoire U tiré de la distribution uniforme sur l'intervalle unité  , La variable aléatoire
, La variable aléatoire
suit une loi exponentielle, où  est la fonction quantile, défini par
est la fonction quantile, défini par
En outre, si U est uniforme sur  , Alors il en est
, Alors il en est  . Cela signifie qu'on peut générer des variables aléatoires exponentielles comme suit:
. Cela signifie qu'on peut générer des variables aléatoires exponentielles comme suit:
Autres méthodes pour générer des variables aléatoires exponentielles sont examinés par Knuth et Devroye.
Le algorithme de ziggourat est une méthode rapide pour générer des variables aléatoires exponentielles.
Distributions connexes
- Une distribution exponentielle est un cas particulier d'un la distribution gamma avec
 (Ou
(Ou  en fonction du jeu de paramètres utilisé).
en fonction du jeu de paramètres utilisé). - À la fois une distribution exponentielle et une distribution gamma sont des cas particuliers de la la distribution de type phase.
 , Soit Y a un Distribution de Weibull, si
, Soit Y a un Distribution de Weibull, si  et
et  . En particulier, toutes les distributions exponentielle est également une distribution de Weibull.
. En particulier, toutes les distributions exponentielle est également une distribution de Weibull.  , Soit Y a un Distribution de Rayleigh, si
, Soit Y a un Distribution de Rayleigh, si  et
et 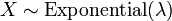 .
.  , Soit Y a un Distribution de Gumbel si
, Soit Y a un Distribution de Gumbel si  et
et 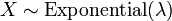 .
.  , Soit Y a un La distribution de Laplace, si
, Soit Y a un La distribution de Laplace, si 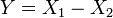 pour deux distributions exponentielles indépendantes
pour deux distributions exponentielles indépendantes 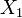 et
et 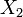 .
.  , Soit Y suit une loi exponentielle si
, Soit Y suit une loi exponentielle si 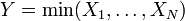 pour les distributions exponentielles indépendantes
pour les distributions exponentielles indépendantes  .
. 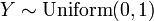 , Soit Y a un distribution uniforme si
, Soit Y a un distribution uniforme si  et
et 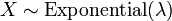 .
.  , C.-à-X a une distribution chi-carré avec deux degrés de liberté, le cas
, C.-à-X a une distribution chi-carré avec deux degrés de liberté, le cas 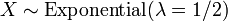 .
. - Laisser
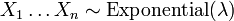 être distribués de façon exponentielle et indépendante
être distribués de façon exponentielle et indépendante  . Puis
. Puis 
 , Puis
, Puis 



![\ Mathrm {} E [X] = \ frac {1} {\ lambda}. \!](../../images/77/7761.png)
![\ Mathrm {} Var [X] = \ frac {1} {\ lambda ^ 2}. \!](../../images/77/7762.png)