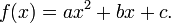Portail: Algèbre
Algèbre

Algèbre est une branche de mathématiques concernant l'étude de la structure , relation et la quantité . Le nom est dérivé du traité écrit par le persan mathématicien, astronome, astrologue et géographe, Muhammad bin Musa al-Khwarizmi intitulé Kitab al-Jabr al-Muqabala (sens " Abrégé du calcul par la restauration et la comparaison "), qui a fourni des opérations pour la solution systématique de linéaire et équation quadratique
Avec la géométrie , l'analyse , la combinatoire et la théorie des nombres , l'algèbre est l'une des principales branches de mathématiques . algèbre élémentaire est souvent partie du programme d'études dans l'enseignement secondaire et fournit une introduction aux idées fondamentales de l'algèbre, y compris les effets de l'ajout et de la multiplication numéros , le concept de variables, définition des polynômes , avec factorisation et la détermination de leur racines.
En plus de travailler directement avec les nombres, l'algèbre couvre travailler avec symboles, variables et fixés éléments. Addition et la multiplication sont considérés comme générale opérations, et leurs définitions précises conduisent à des structures telles que des groupes , anneaux et domaines.
Article sélectionné
 |
| Le graphique d'une valeur réelle fonction quadratique d'une variable réelle x, est un parabole. |
Une équation quadratique est un polynôme équation de deux degrés. La forme générale est
où a ≠ 0 (si a = 0, l'équation devient une équation linéaire ). Les lettres a, b et c sont appelés : coefficients du coefficient quadratique a est le coefficient de x 2, le coefficient linéaire b est le coefficient de x, et c est la coefficient constant, aussi appelé le terme libre.
Équations du second degré sont appelés quadratique parce carré est latine pour "carré"; dans le premier terme est la variable carré.
Une équation quadratique a deux solutions (pas nécessairement distincts), qui peuvent être réel ou complexe , donnés par la formule quadratique:
Ces solutions sont racines du correspondant fonction quadratique
| Crédit image: Enoch Lau |
Saviez-vous?
- ... Qu'il est impossible de concevoir une formule unique ne impliquant que des polynômes et les radicaux pour résoudre un arbitraire quintique équation?
- ... Qu'il est possible pour une figure à trois dimensions pour avoir un fini de volume mais infini surface? Un exemple de ceci est Corne de Gabriel.
- ... Que le Fonction de Gudermann concerne les réguliers fonctions trigonométriques et la fonctions trigonométriques hyperboliques sans l'utilisation de nombres complexes ?
- ... Que le classification des groupes simples finis n'a pas été achevé avant le milieu des années 1980?
- ... Qu'un champ est un structure algébrique dans lequel les opérations de plus , la soustraction , la multiplication et la division (sauf division par zéro) peuvent être effectuées, et les mêmes règles qui détiennent sont familiers de l' arithmétique des ordinaires numéros ?
sous-page

Ceux-ci sont tous les connectés diagrammes de Dynkin, qui classent l'irréductible systèmes racinaires, qui se classent algèbres de Lie simples complexes et simples groupes de Lie complexes. Ces schémas sont donc fondamental tout au long la théorie des groupes de Lie.