Set (mathématiques)

Un ensemble est une collection d'objets distincts pris dans leur ensemble. Les ensembles sont l'un des plus fondamentale concepts dans les mathématiques . L'étude de la structure des ensembles, théorie des ensembles , est riche et continue. Ayant seulement été inventée à la fin du 19ème siècle , la théorie des ensembles est maintenant une partie omniprésente de l'enseignement des mathématiques, étant introduit à partir de l'école primaire dans de nombreux pays. Réglez la théorie peut être considérée comme une base à partir de laquelle la quasi-totalité des mathématiques peuvent être dérivées.

Dans la philosophie , ensembles sont habituellement considérés comme objets abstraits de la physique jetons de qui sont, par exemple; trois tasses sur une table quand on lui parle d'ensemble comme les "tasses", ou les lignes à la craie sur un tableau sous la forme de l'ouverture et de fermeture accolade symboles ainsi que tous les autres symboles dans entre les deux symboles de support. Toutefois, les partisans de réalisme mathématique y compris Penelope Maddy ont fait valoir que les ensembles sont des objets concrets.

L'intersection des deux ensembles est constitué par les objets contenus dans les deux groupes, représentés dans un diagramme de Venn .

Définition

Au début de son der Beiträge zur Begründung transfiniten Mengenlehre, Georg Cantor , le principal créateur de la théorie des ensembles, a donné la définition suivante d'un ensemble:

Par un «ensemble», nous entendons toute collection M dans un ensemble d'objets définis, distincts m (que l'on appelle les «éléments» de M) de notre perception [Anschauung] ou de notre pensée.

Le éléments d'un ensemble, aussi appelé ses membres, peuvent être ne importe quoi: des chiffres, des personnes, des lettres de l'alphabet, d'autres ensembles, et ainsi de suite. Ensembles sont classiquement désignées par lettres majuscules. L'instruction qui définit A et B sont égaux signifie qu'ils ont exactement les mêmes membres (c.-à chaque membre de A est aussi un membre de B et vice versa).

Contrairement à un multiset, chaque élément d'un ensemble doit être unique; pas deux membres peuvent être identiques. Toutes les opérations de réglage de préserver la propriété qui est chaque élément de l'ensemble unique. L'ordre dans lequel les éléments d'un ensemble sont énumérés ne est pas pertinent, contrairement à une séquence ou tuple.

Décrire ensembles

Il ya deux façons de décrire, ou de spécifier les membres de, un ensemble. Une solution est de définition intensionnelle, en utilisant une règle ou description sémantique. Voir cet exemple:

A est l'ensemble dont les membres sont les quatre premiers positifs entiers .

B est l'ensemble des couleurs de la Drapeau français.

La deuxième façon est de extension, qui est, énumérant chaque membre de l'ensemble. Une définition générique est noté en enfermant la liste des membres en accolades:

{C = 4, 2, 1, 3}

D = {bleu, blanc, rouge}

L'ordre dans lequel les éléments d'un ensemble sont répertoriés dans une définition d'extension ne est pas pertinent, tout comme les répétitions dans la liste. Par exemple,

{6, 11} = {11, 6} = {11, 11, 6, 11}

sont équivalentes, parce que la spécification d'extension signifie simplement que chacun des éléments énumérés est un élément de l'ensemble.

Pour les jeux avec de nombreux éléments, l'énumération des membres peut être abrégé. Par exemple, l'ensemble des mille premiers nombres entiers positifs peut être spécifié extensionnellement que:

{1, 2, 3, ..., 1000},

où le points de suspension («...») indique que la liste continue de manière évidente. Ellipses peuvent également être utilisé où les jeux ont une infinité de membres. Ainsi l'ensemble des positifs même numéros peuvent être écrites comme {2, 4, 6, 8, ...}.

La notation avec accolades peut également être utilisé dans une spécification intension d'un ensemble. Dans cette utilisation, les accolades ont la signification "l'ensemble de tous ..." Alors E = {costumes jeu de cartes} est l'ensemble dont les quatre membres sont ♠, ♦, ♥, et ♣. Une forme plus générale de ce est notation set-constructeur, à travers laquelle, par exemple, l'ensemble F des vingt plus petits entiers qui sont quatre de moins que carrés parfaits peuvent être notées:

F = {n ^2-4: n est un nombre entier; et 0 ≤ n ≤ 19}

Dans cette notation, le deux points (":") signifie "tel que", et la description peut être interprété comme "F est l'ensemble de tous les nombres de la forme n ^2-4, tel que n est un nombre entier dans la plage de 0 à 19 inclusivement ». Parfois, la barre verticale ("|") est utilisé à la place du côlon.

On a souvent le choix de spécifier un ensemble intensionnellement ou extensionnellement. Dans les exemples ci-dessus, par exemple, A = C et B = D.

Adhésion

Si quelque chose est ou ne est pas un élément d'un ensemble particulier alors ce est symbolisée par ∈ et ∉ respectivement. Ainsi, en ce qui concerne les ensembles définis ci-dessus:

• 4 ∈ A et 285 ∈ F (depuis 285 = 17² - 4); mais
• 9 ∉ F et vert ∉ B.

Cardinalité

Le cardinal | S | d'un ensemble S est ". Le nombre de membres de S" Par exemple, depuis le pavillon français a trois couleurs, | B | = 3.

Il ya un ensemble sans membres et cardinalité zéro, ce qui est appelé le ensemble vide (ou l'ensemble vide) et est désigné par le symbole ø. Par exemple, l'ensemble A de tous les carrés à trois côtés a zéro membres (| A | = 0), et donc A = ø. Bien que, comme le numéro zéro , il peut sembler trivial, l'ensemble vide est très important en mathématiques. L'existence de cet ensemble est l'un des concepts fondamentaux de la théorie des ensembles axiomatique .

Certains jeux ont infinie cardinal. L'ensemble N des nombres naturels , par exemple, est infini. Certaines cardinalités infinies sont plus que d'autres. Par exemple, l'ensemble des nombres réels a une plus grande cardinal que l'ensemble des nombres naturels. Cependant, il peut être démontré que le cardinal de (ce est-à-dire le nombre de points sur) une ligne droite est le même que le cardinal de toute tronçon de cette ligne, d'un ensemble avion, et même de tout l'espace euclidien .

Sous-ensembles

Si chaque membre de l'ensemble A est également un membre de l'ensemble B, alors A est dit être un sous-ensemble de B, écrit (Également prononcé A est contenu dans B). Équivalente, nous pouvons écrire , Lire comme B est un sur-ensemble de A, B comprend A, ou B contient A. Le relation entre les séries établies par 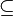est appelé inclusion ou de confinement.

Si A est un sous-ensemble de, mais pas égal à B, alors A est appelé un sous-ensemble de B, écrit (A est un sous-ensemble propre de B) ou (B est bonne sur-ensemble de A).

On notera que les expressions et sont utilisés différemment par différents auteurs; certains auteurs utilisent pour signifier la même que (Respectivement ), Tandis que d'autres les utiliser pour le même sens que (Respectivement ).

A est un sous-ensemble de B

Exemple:

• L'ensemble de tous les hommes est un sous-ensemble de l'ensemble de toutes les personnes.
• 
• 

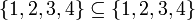
L'ensemble vide est un sous-ensemble de chaque jeu et chaque ensemble est un sous-ensemble de lui-même:

jeu de puissance

L'ensemble d'un ensemble S de puissance peut être défini comme l'ensemble de tous les sous-ensembles de S. Cela inclut les sous-ensembles formés à partir des membres du S et l'ensemble vide. Si un ensemble fini S est de cardinal n alors l'ensemble des S de puissance a cardinalité 2 ^n. Si S est un infini (soit dénombrable ou uncountable) mis alors l'ensemble des S de puissance est toujours innombrables. Le jeu de puissance peut être écrit comme deux ^S.

A titre d'exemple, la puissance réglée 2 ^{{1, 2, 3}} de {1, 2, 3} est égal à l'ensemble {{1, 2, 3}, {1, 2}, {1, 3}, { 2, 3}, {1}, {2}, {3}, ø}. Le cardinal de l'ensemble original est trois, et le cardinal de l'ensemble d'alimentation est 2 ³ ou 8. Cette relation est une des raisons pour le jeu de puissance de la terminologie. De même, sa notation est un exemple d'une convention générale fournissant notations pour les jeux en fonction de leurs cardinalités.

Des ensembles spéciaux

Il ya quelques jeux qui détiennent une grande importance mathématique et sont considérés avec une telle régularité qu'ils ont acquis des noms spéciaux et des conventions de notation pour les identifier. L'un d'eux est l'ensemble vide. Beaucoup de ces ensembles sont représentés en utilisant Blackboard caractères gras. Ensembles spéciales de chiffres incluent:

• , Représentant l'ensemble de tous les nombres premiers .
• , Désignant l'ensemble des nombres naturels . C'est-à-dire, = {1, 2, 3, ...}, ou parfois = {0, 1, 2, 3, ...}.
• , Représentant l'ensemble de tous les nombres entiers (positive, négative ou nulle). Si = {..., -2, -1, 0, 1, 2, ...}.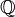
• , Représentant l'ensemble de tous les nombres rationnels (ce est l'ensemble de toutes appropriées et des fractions impropres ). Alors, 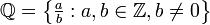. Par exemple, et . Tous sont des nombres entiers dans cet ensemble tout entier depuis un peut être exprimé comme la fraction .
• , Désignant l'ensemble des nombres réels . Cet ensemble comprend tous les nombres rationnels, ainsi que toutes irrationnelles nombres (ce est le nombre qui ne peut être réécrite sous forme de fractions, comme et √2).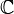
• , Représentant l'ensemble de tous les nombres complexes .

Chacun de ces ensembles de nombres a un nombre infini d'éléments, et 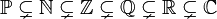. Les nombres premiers sont utilisés moins fréquemment que les autres en dehors de la théorie des nombres et des domaines connexes.

Opérations de base

Unions

Il ya plusieurs façons de construire de nouveaux ensembles de celles existantes. Deux ensembles peuvent être "ajoutés" ensemble. L'union de A et B, notée A ∪ B, est l'ensemble de toutes les choses qui sont membres de A ou B.

L'union de A et B

Exemples:

• {1, 2} ∪ {rouge, blanc} = {1, 2, rouge, blanc}
• {1, 2, vert} ∪ {rouge, blanc, vert} = {1, 2, rouge, blanc, vert}
• {1, 2} ∪ {1, 2} = {1, 2}

Certaines propriétés de base des syndicats sont:

• A ∪ B = B ∪ A
• A ⊆ (A ∪ B)
• A ∪ A = A
• A ∪ ø = A
• A ⊆ B si et seulement si A ∪ B = B

Intersections

Un nouvel ensemble peut également être construit par déterminer quels membres deux ensembles ont «en commun». L'intersection de A et B, notée A ∩ B, est l'ensemble de toutes les choses qui sont membres à la fois A et B. Si A ∩ B = O, alors A et B sont dits disjoints.

L'intersection de A et B

Exemples:

• {1, 2} ∩ {rouge, blanc} = ø
• {1, 2, vert} ∩ {rouge, blanc, vert} = {} verte
• {1, 2} ∩ {1, 2} = {1, 2}

Certaines propriétés de base des intersections:

• A ∩ B = B ∩ A
• A ∩ B ⊆ A
• A ∩ A = A
• A ∩ = ø ø
• A ⊆ B si et seulement si A ∩ B = A

Compléments

Deux séries peuvent également être «soustraits». Le complément relatif de A dans B (également appelé la différence ensembliste de B et A), notée B \ A (ou B - A) est l'ensemble de tous les éléments qui sont membres de B, mais pas membres d'un. Notez qu'il est valide pour «soustraire» membres d'un jeu qui ne sont pas dans le jeu, telles que la suppression vert de {1,2,3}; faisant n'a aucun effet.

Dans certains paramètres tous les jeux en cours de discussion sont considérés comme des sous-ensembles d'une donnée universal U. Dans de tels cas, U \ A, est appelé le complément absolue ou simplement compléter de A, et est noté A '.

Le complément relatif
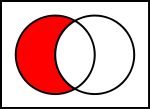
de A dans B

Le complément d'un U en

Exemples:

• {1, 2} \ {rouge, blanc} = {1, 2}
• {1, 2, vert} \ {rouge, blanc, vert} = {1, 2}
• {1, 2} \ {1, 2} = ∅
• Si U est l'ensemble des entiers, E est l'ensemble des entiers pairs, et O est l'ensemble des nombres impairs, alors le complément de E dans U est O, ou de manière équivalente, E '= O.

Certaines propriétés de base de compléments:

• A ∪ A '= U
• A ∩ A '= ∅
• (A ')' = A
• A \ A = ∅
• A \ B = A ∩ B '

Produit cartésien

Un nouvel ensemble peut être construite en associant tous les éléments d'un ensemble avec tous les éléments d'un autre ensemble. Le produit cartésien de deux ensembles A et B, notée A × B est l'ensemble de toutes couples (a, b) de telle sorte que A est un élément de A et B est un membre de B.

Exemples:

• {1, 2} x {rouge, blanc} = {(1, rouge), (1, blanc), (2, rouge), (2, blanc)}
• {1, 2, vert} × {rouge, blanc, vert} = {(1, rouge), (1, blanc), (1, vert), (2, rouge), (2, blanc), (2, vert), (vert, rouge), (vert, blanc), (vert, vert)}
• {1, 2} x {1, 2} = {(1,1), (1,2), (2,1), (2,2)}

Certaines propriétés de base des produits cartésiens:

• A × ∅ = ∅
• A × (B ∪ C) = (A × B) ∪ (A × C)
• | A × B | = | A | × | B |

Applications

La théorie des ensembles est considéré comme la fondation à partir de laquelle la quasi-totalité des mathématiques peuvent être dérivées. Par exemple, les structures de l'algèbre abstraite , comme les groupes , champs et anneaux, sont des ensembles fermés sous une ou plusieurs opérations.

L'une des principales applications de la théorie naïve des ensembles construit relations. A partir d'une relation Un domaine à un codomain B ne est qu'un sous-ensemble de A × B. Compte tenu de ce concept, nous sommes prompts à voir que l'ensemble F de tous ordonné paires (x, x ^2), où x est réel, est assez familier. Il dispose d'un ensemble de domaine et un ensemble d'arrivée fixé qui est aussi , Parce que l'ensemble de tous les carrés est sous-ensemble de l'ensemble des nombres réels. Se il est placé en notation fonctionnelle, cette relation devient f (x) = x ^2. La raison pour laquelle ces deux sont équivalents est à une valeur donnée, la fonction qui y est définie pour, une paire ordonnée correspondante, (y, y ²⁾ est un élément de l'ensemble F.

La théorie des ensembles axiomatique

Bien qu'initialement le la théorie naïve des ensembles, qui définit un ensemble simplement comme toute collection bien définie, a été bien accepté, il est vite couru dans plusieurs obstacles. Il a été constaté que cette définition engendré plusieurs paradoxes, et plus particulièrement:

• Le paradoxe de Russell - Il montre que "l'ensemble de tous les ensembles qui ne contiennent pas eux-mêmes," ce est à dire le "set" 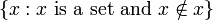n'existe pas.
• Paradoxe de Cantor - Il montre que "l'ensemble de tous les ensembles" ne peut pas exister.

La raison en est que l'expression bien définie ne est pas très bien définie. Il était important à la libre théorie des ensembles de ces paradoxes, car la quasi-totalité des mathématiques a été redéfinis en termes de la théorie des ensembles. Dans une tentative pour éviter ces paradoxes, la théorie des ensembles a été axiomatisé basée sur la logique du premier ordre , et donc la théorie des ensembles axiomatique est né.

Pour la plupart des applications cependant, la la théorie des ensembles naïve est toujours utile.

Réalisme mathématique

Penelope Maddy a suggéré que les ensembles peuvent être causalement efficace, et en fait part toute la causalité et les propriétés spatio-temporelles de leurs éléments. Ainsi, quand je vois les trois tasses sur la table en face de moi, je vois aussi l'ensemble ainsi. Elle a utilisé les travaux récents en sciences cognitives et de la psychologie de soutenir cette position, soulignant que, tout comme à un certain âge, nous commençons à voir les objets plutôt que de simples perceptions sensorielles, il ya aussi un certain âge à laquelle nous commençons à voir des ensembles plutôt que de simplement objets.