Distribution de probabilité

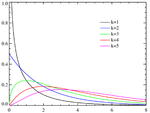
Une distribution de probabilité décrit les valeurs et les probabilités qu'une événement aléatoire peut avoir lieu. Les valeurs doivent couvrir l'ensemble des résultats possibles de l'événement, alors que le total doit probabilités totaliser exactement 1, ou 100%. Par exemple, un seul coin flip peut prendre des valeurs Heads or Tails avec une probabilité de 1/2 exactement pour chaque; ces deux valeurs et deux probabilités représentent la distribution de probabilité de l'événement pièce de retournement unique. Cette distribution se appelle une distribution discrète car il ya nombre dénombrable de résultats discrets avec des probabilités positives.

Une distribution continue décrit les événements sur une plage continue, où la probabilité d'un résultat spécifique est zéro. Par exemple, une fléchette lancée à un jeu de fléchettes a essentiellement une probabilité nulle de l'atterrissage à un moment précis, car un point est extrêmement faible, mais il a une certaine probabilité de l'atterrissage dans une zone donnée. La probabilité de l'atterrissage dans la petite zone de la bulle serait (je espère) être supérieur à l'atterrissage sur une superficie équivalente ailleurs sur la carte. Une fonction lisse qui décrit la probabilité d'atterrir ne importe où sur la cible est la distribution de probabilité de l'événement de lancement de fléchettes. L' intégrale de la fonction de densité de probabilité (pdf) sur toute la surface de la cible (et, peut-être, le mur qui l'entoure) doit être égale à 1, puisque chaque fléchette doit atterrir quelque part.

Le concept de la distribution de probabilité et les variables aléatoires qu'ils décrivent sous-tend la discipline mathématique de la théorie des probabilités , et la science des statistiques . Il est réparti ou de la variabilité dans presque ne importe quelle valeur qui peut être mesurée dans une population (par exemple taille des gens, la durabilité d'un métal, etc.); presque toutes les mesures sont faites avec une certaine erreur intrinsèque; dans la physique de nombreux procédés sont décrits de manière probabiliste, à partir de la propriétés cinétiques de gaz à la mécanique quantique description de particules fondamentales. Pour ces raisons et bien d'autres, simples numéros sont souvent insuffisants pour décrire une quantité, tandis que les distributions de probabilité sont souvent des modèles plus appropriés. Il ya, cependant, des complications mathématiques dans la manipulation des distributions de probabilité, depuis plus standard arithmétique et manipulations algébriques ne peuvent pas être appliquées.

Définitions rigoureuses

Dans la théorie des probabilités , chaque variable aléatoire peut être attribuée à une fonction définie sur un espace d'état équipé d'une distribution de probabilité qui assigne une probabilité à chaque sous-ensemble (plus précisément chaque sous-ensemble mesurable) de son espace d'état de telle sorte que le axiomes de probabilité sont satisfaits. Ce est, distributions de probabilité sont mesures de probabilité définies sur un espace à la place de l'Etat de l'espace échantillon. Une variable aléatoire définit alors une mesure de probabilité sur l'espace de l'échantillon en attribuant un sous-ensemble de l'espace de l'échantillon la probabilité de son image inverse dans l'espace d'état. En d'autres termes, la distribution de probabilité d'une variable aléatoire est la faire avancer mesure de la distribution de probabilité sur l'espace d'état.

Les distributions de probabilité de variables aléatoires valeur réelle

Parce que une distribution de probabilité Pr sur la ligne réelle est déterminée par la probabilité d'être dans un intervalle semi-ouvert Pr (a, b], la distribution de probabilité d'une variable aléatoire à valeur réelle X est complètement caractérisée par son fonction de distribution cumulative:

Distribution de probabilité discrète

Une distribution de probabilité est appelé discrète si sa fonction de distribution cumulative ne augmente que dans les sauts.

Le ensemble des valeurs qu'une variable aléatoire discrète peut assumer non nulle probabilité est soit fini ou dénombrable infinie car la somme de indénombrablement nombreux positifs nombres réels (qui est la plus petite borne supérieure de l'ensemble des sommes partielles finies) diverge toujours à l'infini. En règle générale, l'ensemble des valeurs possibles est topologiquement discret en ce sens que tous ses points sont points isolés. Mais, il ya des variables aléatoires discrètes pour lequel ce est ensemble dénombrable dense sur la ligne réelle.

Distributions discrètes sont caractérisés par une Fonction de masse, 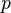tel que

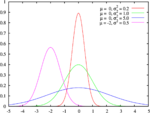
La distribution de probabilité continue

Par une convention, une distribution de probabilité est appelée en continu si sa fonction de distribution cumulative est continu, ce qui signifie qu'elle appartient à une variable aléatoire X pour laquelle Pr [X = x] = 0 pour tout x dans R.

Une autre convention se réserve la distribution de probabilité continue à long terme pour distributions absolument continue. Ces distributions peuvent être caractérisés par un fonction de densité de probabilité: un non-négative intégrable Lebesgue fonction défini sur les nombres réels tels que

Distributions discrètes et certaines distributions continues (comme le l'escalier du diable) ne admet pas une telle densité.

Terminologie

Le soutien d'une distribution est le plus petit ensemble fermé dont le complément a une probabilité nulle.

La distribution de probabilité de la somme de deux variables aléatoires indépendantes est le convolution de chacun de leurs distributions.

La distribution de probabilité de la différence de deux variables aléatoires est la corrélation croisée de chacun de leurs distributions.

Une variable aléatoire discrète est une variable aléatoire dont la distribution probabilité est discrète. De même, une variable aléatoire continue est une variable aléatoire dont la loi de probabilité est continue.

Liste des distributions de probabilité importants

Certaines variables aléatoires apparaissent très souvent dans la théorie des probabilités, dans certains cas, en raison de leur application à de nombreux phénomènes naturels et physiques, et dans certains cas pour des raisons théoriques telles que la théorème central limite, le Poisson théorème de la limite ou des propriétés telles que Perte de mémoire ou d'un autre caractérisations. Leurs distributions ont donc pris une importance particulière dans la théorie des probabilités.

Distributions discrètes

Avec support fini

• Le Distribution de Bernoulli, qui prend la valeur 1 avec une probabilité p et la valeur 0 avec une probabilité q = 1 - p.
• Le Loi de Rademacher, qui prend la valeur 1 avec une probabilité 1/2 et la valeur -1 avec une probabilité 1/2.
• La distribution binomiale décrit le nombre de succès dans une série d'indépendants Oui / Non expériences.
• Le la distribution dégénérée en x _0, où X est certain de prendre la valeur ₀ x. Cela ne ressemble pas au hasard, mais il répond à la définition de variable aléatoire . Il est utile parce qu'il met des variables et des variables aléatoires déterministes dans le même formalisme.
• Le distribution uniforme discrète, où tous les éléments d'un fini ensemble sont également probables. Ce est censé être la distribution d'une pièce équilibrée, une filière impartiale, une roulette de casino ou un jeu bien mélangé. Aussi, on peut utiliser des mesures de états quantiques pour générer des variables aléatoires uniformes. Tous ces dispositifs sont «mécaniques» «physique» ou, sous réserve de défauts de conception ou de perturbations, de sorte que la distribution uniforme ne est qu'une approximation de leur comportement. Dans les ordinateurs numériques, générateurs de nombres pseudo-aléatoires sont utilisées pour produire un la distribution uniforme discrète statistiquement aléatoire.
• Le distribution hypergéométrique, qui décrit le nombre de succès dans la première m d'une série de n Oui / Non expériences, si le nombre total de succès est connue.
• La loi de Zipf ou la distribution Zipf. Une distribution en loi de puissance discrète, le plus célèbre exemple est la description de la fréquence des mots dans la langue anglaise.
• Le La loi de Zipf-Mandelbrot est une distribution de loi de puissance discrète qui est une généralisation de la La distribution Zipf.

Avec le soutien infinie

• Le Distribution de Boltzmann, une distribution discrète important physique statistique qui décrit les probabilités des différents niveaux d'énergie discrets d'un système de équilibre thermique. Il dispose d'un analogue continu. Cas particuliers comprennent:
  • Le Distribution de Gibbs
  • Le Distribution de Maxwell-Boltzmann
  • Le La distribution de Bose-Einstein
  • Le Distribution de Fermi-Dirac
• Le distribution géométrique, une distribution discrète qui décrit le nombre de tentatives nécessaires pour obtenir le premier succès dans une série d'indépendants Oui / Non expériences.

Distribution de Poisson

• Le logarithmique (série) la distribution
• Le distribution binomiale négative, une généralisation de la distribution géométrique de la n-ième succès
• Le la distribution fractale parabolique
• La distribution de Poisson , qui décrit un très grand nombre d'événements improbables individuellement qui se produisent dans un certain intervalle de temps.

Loi de Skellam

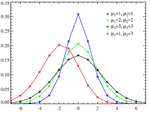
• Le Loi de Skellam, la distribution de la différence entre deux variables aléatoires de Poisson indépendantes distribuée
• Le Loi de Yule-Simon
• Le Répartition zeta a des utilisations en statistique appliquée et mécanique statistique, et peut-être peut être d'intérêt pour les théoriciens des nombres. C'est le Zipf pour la distribution d'un nombre infini d'éléments.

Distributions continues

Pris en charge sur un intervalle borné

Loi bêta

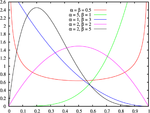
• Le Loi bêta sur [0,1], dont la distribution uniforme est un cas particulier, et qui est utile dans l'estimation des probabilités de réussite.

distribution uniforme continu

• Le la distribution uniforme continue sur [a, b], où tous les points dans un intervalle fini sont également probables.
  • Le distribution rectangulaire est une distribution uniforme sur [-1 / 2,1 / 2].
• Le Dirac bien que pas strictement une fonction, est une forme de limitation de beaucoup de fonctions continues de probabilité. Elle représente une distribution de probabilité discrète concentré à 0 - un la distribution dégénérée - mais la notation traite comme se il se agissait d'une distribution continue.
• Le Loi de Kent sur la sphère en trois dimensions
• Le Loi Kumaraswamy est aussi polyvalent que la distribution Beta mais a formes fermées simples à la fois pour la cdf et pdf.
• Le la distribution logarithmique (continue)
• Le distribution triangulaire sur [a, b], un cas particulier de ce qui est de la distribution de la somme de deux variables aléatoires réparties uniformément (la convolution de deux distributions uniformes).
• Le distribution normale tronquée sur [a, b]
• Le Loi parabolique sur [a, b]
• Le Loi de von Mises sur le cercle
• Le Loi de von Mises-Fisher sur la sphère à N dimensions a le Loi de von Mises comme un cas particulier.
• Le Loi du demi-cercle est important dans la théorie de matrices aléatoires.

Pris en charge sur des intervalles semi-infinies, habituellement [0, ∞)

la distribution chi-carré

• Le la distribution chi
• Le distribution chi non centrale
• La distribution chi-carré , qui est la somme des carrés des variables aléatoires gaussiennes n indépendants. Ce est un cas particulier de la distribution Gamma, et il est utilisé dans tests dans la bonté de l'ajustement des statistiques .
  • Le Inverse Chi-carré de distribution
  • Le chi carré non centrale de distribution
  • Le échelle inverse chi carré la distribution

Distribution exponentielle

• La distribution exponentielle , qui décrit le temps entre des événements aléatoires rares consécutives dans un processus sans mémoire.
• Le F-distribution, qui est la distribution du rapport de deux variables aléatoires (normalisé) chi-carrés répartis, utilisé dans le analyse de la variance. (Appelé Loi bêta prime quand il est le rapport de deux variables chi-carré qui ne sont pas normalisés en les divisant par le nombre de leurs degrés de liberté.)
  • Le F non centrale de distribution

Distribution Gamma

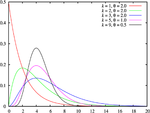
• Le Distribution Gamma, qui décrit le temps jusqu'à ce que des événements aléatoires n rares consécutifs se produisent dans un processus sans mémoire.
  • Le Distribution d'Erlang, qui est un cas particulier de la distribution gamma avec le paramètre de forme intégrale, développé pour prédire les temps d'attente dans systèmes de files d'attente.
  • Le la distribution gamma inverse
• Le distribution normale pliée
• Le Répartition de la moitié de la normale
• Le distribution gaussienne inverse, aussi connue comme la distribution Wald
• Le Loi de Lévy
• Le la distribution log-logistique
• Le la distribution log-normale, décrivant les variables qui peuvent être modélisées comme le produit de nombreuses petites variables positives indépendants.

Distribution de Pareto

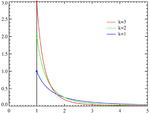
• Le Distribution de Pareto, ou la distribution de "loi de puissance", utilisée dans l'analyse des données financières et comportement critique.
• La distribution de Pearson de type III (voir Distributions Pearson)
• Le Distribution de Rayleigh
• Le Distribution de Rayleigh mélange
• Le Distribution de Rice
• Le Rosin Rammler de distribution - utilisé pour décrire le Répartition de la taille des particules de particules générées par broyage, fraisage et opérations de concassage.
• Le distribution de Gumbel type 2
• Le Distribution de Weibull, dont la distribution exponentielle est un cas particulier, est utilisé pour modéliser la durée de vie des dispositifs techniques.

Pris en charge sur toute la ligne réelle

Distribution de Cauchy

La distribution de Laplace

La distribution Levy

Distribution normale

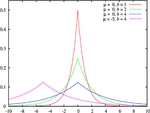
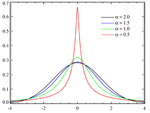
• Le Distribution de Cauchy, un exemple d'une distribution qui ne ont pas un valeur attendue ou d'une variance . En physique, il est généralement appelé Profil de Lorentz, et est associée à de nombreux procédés, y compris la distribution d'énergie de résonance, l'impact et naturel élargissement de la raie spectrale et quadratique Stark élargissement de ligne.
• Le Fisher-Tippett, valeur extrême, ou connectez-Weibull la distribution
  • Le Distribution de Gumbel, un cas particulier de la distribution de Fisher-Tippett
• Loi z de Fisher
• Le distribution des valeurs extrêmes généralisée
• Le la distribution hyperbolique
• Le répartition sécante hyperbolique
• Le Loi de Landau
• Le La distribution de Laplace
• Le La distribution alpha-stable biais Lévy est souvent utilisé pour caractériser les données financières et comportement critique.
• Le carte de distribution-Airy
• La distribution normale , aussi appelé le Gauss ou la courbe en cloche. Il est omniprésent dans la nature et les statistiques en raison de la théorème central limite: chaque variable qui peut être modélisée comme une somme de nombreux petits variables indépendantes est à peu près normale.
• Le Distribution de Pearson de type IV (voir Distributions Pearson)
• Loi de Student , utile pour estimer des moyens inconnus des populations gaussiennes.
  • Le distribution t non centrale
• Le distribution de Gumbel type 1
• Le Répartition Voigt, ou profil Voigt, est la convolution d'une distribution normale et une Distribution de Cauchy. On le trouve dans la spectroscopie lorsque les profils de raies spectrales sont élargies par un mélange de Lorentz et Doppler mécanismes élargir.

Distributions conjointes

Pour tout ensemble de variables aléatoires indépendantes du fonction de densité de probabilité de leur distribution conjointe est le produit de leurs fonctions individuelles de densité.

distributions Matrix-évalué

• Distribution de Wishart
• distribution normale matrice
• matrice distribution t
• T-carré de la distribution de Hotelling