
Trou noir
Saviez-vous ...
Enfants SOS ont produit une sélection d'articles de wikipedia pour les écoles depuis 2005. SOS enfants est le plus grand organisme de bienfaisance dans le monde en donnant aux enfants orphelins et abandonnés la chance de la vie familiale.

| La relativité générale |
|---|
 |
| Introduction Formulation mathématique Ressources |
Concepts fondamentaux |
|
Phénomènes Problème de Kepler · Objectifs · Flots Cadre traîner · Effet géodésique Event horizon · Singularité Trou noir |
Équations Approximation des champs faibles Formalisme post-newtonien Équation d'Einstein Équation géodésique Équations de Friedmann Formalisme ADM BSSN formalisme Équation de Hamilton-Jacobi-Einstein |
Théories avancées Kaluza-Klein La gravité quantique |
Solutions Schwarzschild Reissner-Nordström · Gödel Kerr · Kerr-Newman Kasner · Taub-NUT · Milne · Robertson-Walker pp-ondes · la poussière van Stockum |
Les scientifiques Einstein · Lorentz · Hilbert · Poincaré · Schwarzschild · · Sitter Reissner · Nordström · Weyl · Eddington · Friedman · Milne · Zwicky · Lemaître · Gödel · Wheeler · Robertson · Bardeen · Walker · Kerr · Chandrasekhar · Ehlers · Penrose · Hawking · Taylor · Hulse · Stockum · Taub · Nouvel Homme Yau · Thorne autres |
Spacetime Spacetime Minkowski espace-temps diagrammes de Spacetime Spacetime en relativité générale |
Un trou noir est une région de l'espace-temps à partir de laquelle la gravité empêche quoi que ce soit, y compris la lumière , de se échapper. La théorie de la relativité générale prédit que suffisamment compacte masse se déforme l'espace-temps pour former un trou noir. Autour d'un trou noir il ya une surface définie mathématiquement appelé horizon d'événement qui marque le point de non-retour. Il est appelé "noir" parce qu'il absorbe toute la lumière qui frappe l'horizon, ce qui reflète rien, juste comme un parfait corps noir de la thermodynamique . La théorie quantique des champs en espace courbe prédit que horizons d'événements émettent un rayonnement comme un corps noir avec un fini température . Cette température est inversement proportionnelle à la masse du trou noir, ce qui rend difficile à observer ce rayonnement pour trous noirs de masse stellaire ou supérieure.
Objets dont champ de gravité est trop forte pour la lumière de se échapper ont d'abord examiné dans le 18ème siècle par John Michell et Pierre-Simon Laplace . La première solution moderne de la relativité générale qui permette de caractériser un trou noir a été trouvé par Karl Schwarzschild en 1916, bien que son interprétation comme une région de l'espace à partir de laquelle rien ne peut échapper ne était pas pleinement apprécié pendant encore quatre décennies. Longtemps considéré comme une curiosité mathématique, ce est durant les années 1960 que le travail théorique a montré trous noirs étaient une prédiction générique de la relativité générale. La découverte de étoiles à neutrons ont suscité intérêt gravitationnellement effondré objets compacts comme une réalité possible astrophysiques.
Les trous noirs de masse stellaire sont censés se former lorsque étoiles très massives effondrement à la fin de leur cycle de vie. Après un trou noir a formé, il peut continuer à croître en absorbant la masse de ses environs. En absorbant d'autres étoiles et de fusionner avec d'autres trous noirs, trous noirs supermassifs de millions de masses solaires peuvent se former. Il est généralement admis que les trous noirs supermassifs existent dans les centres de la plupart des galaxies .
Malgré son intérieur invisible, la présence d'un trou noir peut être déduite grâce à son interaction avec d'autres matières et avec un rayonnement électromagnétique comme la lumière. Matière tomber sur un trou noir peut former un disque d'accrétion chauffée par friction, ils font partie des objets les plus brillants dans l'univers. Se il ya d'autres étoiles en orbite autour d'un trou noir, leur orbite peut être utilisée pour déterminer sa masse et l'emplacement. Ces données peuvent être utilisées pour exclure les alternatives possibles (tels que les étoiles à neutrons). De cette façon, les astronomes ont identifié de nombreux stellaires candidats trous noirs dans les systèmes binaires , et a établi que le noyau de notre Voie Lactée galaxie contient un trou noir supermassif d'environ 4,3 millions masses solaires.
Histoire

L'idée d'un corps si massif que même la lumière ne pouvait pas échapper a d'abord été mis en avant par géologue John Michell dans une lettre écrite à Henry Cavendish en 1783 de la Société royale:
Si le demi-diamètre d'une sphère de la même densité que le Soleil devait être supérieure à celle du Soleil dans la proportion de 500 à 1, un corps en chute libre d'une hauteur infinie vers elle aurait acquis à sa surface plus grande vitesse que celle de la lumière, et la lumière en supposant par conséquent à être attiré par la même force en proportion de sa force d'inertie, avec d'autres organismes, toute la lumière émise à partir d'un tel organisme serait fait pour revenir vers lui par sa propre gravité appropriée.-John Michell
En 1796, le mathématicien Pierre-Simon Laplace promu la même idée dans les première et deuxième éditions de son livre Exposition du système du monde (il a été retiré des éditions ultérieures). Un tel " étoiles noires "ont été largement ignorés au XIXe siècle, car il ne était pas compris comment une vague sans masse comme la lumière pourrait être influencée par la gravité.
La relativité générale
En 1915, Albert Einstein a développé sa théorie de la relativité générale , après avoir montré plus tôt que la gravité fait la motion de l'influence de la lumière. Seulement quelques mois plus tard, Karl Schwarzschild trouvé un solution de Einstein Les équations de champ, qui décrit la d'un champ gravitationnel point de masse et une masse sphérique. Quelques mois après Schwarzschild, Johannes Droste, un étudiant de Hendrik Lorentz, indépendamment a la même solution pour la masse de points et a écrit plus largement sur ses propriétés. Cette solution a un comportement particulier à ce qui est maintenant appelé le Rayon de Schwarzschild, où il est devenu singulier, ce qui signifie que certains des termes dans les équations d'Einstein est devenu infini. La nature de cette surface ne était pas tout à fait compris à l'époque. En 1924, Arthur Eddington a montré que la singularité a disparu après un changement de coordonnées (voir Coordonnées Eddington-Finkelstein), même se il a fallu attendre 1933 pour Georges Lemaître se rendre compte que cela signifiait la singularité au rayon de Schwarzschild était un non physique coordonner singularité.
En 1931, Subrahmanyan Chandrasekhar calculé, en utilisant la relativité restreinte, qu'un corps non tournante la matière électronique dégénérée dessus d'une certaine masse limite (maintenant appelé le Limite de Chandrasekhar à 1,4 masses solaires) n'a pas de solutions stables. Ses arguments étaient opposés par beaucoup de ses contemporains comme Eddington et Lev Landau, qui a fait valoir que certains mécanisme encore inconnu pourrait arrêter l'effondrement. Ils étaient en partie raison: une naine blanche légèrement plus massive que la limite de Chandrasekhar va se effondrer dans un étoile à neutrons, qui est lui-même stable en raison de la Principe d'exclusion de Pauli. Mais en 1939, Robert Oppenheimer et d'autres ont prédit que les étoiles à neutrons ci-dessus environ trois masses solaires (la Limite d'Oppenheimer-Volkoff) se effondrerait dans les trous noirs pour les raisons présentées par Chandrasekhar, et a conclu qu'aucune loi de la physique était susceptible d'intervenir et d'arrêter au moins quelques étoiles de se effondrer aux trous noirs.
Oppenheimer et ses co-auteurs ont interprété la singularité à la limite du rayon de Schwarzschild comme indiquant que ce était la limite d'une bulle dans laquelle temps se est arrêté. Ce est un point de vue pour les observateurs externes valide, mais pas pour infalling observateurs. En raison de cette propriété, les étoiles effondrées ont été appelés «étoiles gelés», parce qu'un observateur extérieur verrait la surface de l'étoile figé dans le temps à l'instant où son effondrement prend à l'intérieur du rayon de Schwarzschild.
Age d'Or
En 1958, David Finkelstein la surface identifiée comme une Schwarzschild horizon des événements, "une membrane unidirectionnel parfaite: influences causales peuvent traverser dans une seule direction". Ce ne contredisait pas strictement les résultats de Oppenheimer, mais leur étendue pour inclure le point de vue de infalling observateurs. La solution de Finkelstein étendu la solution de Schwarzschild pour l'avenir des observateurs de tomber dans un trou noir. Un l'extension complète avait déjà été trouvé par Martin Kruskal, qui a été invité à publier.
Ces résultats ont été obtenus au début de la âge d'or de la relativité générale, qui a été marquée par la relativité générale et les trous noirs deviennent sujets traditionnels de recherche. Ce processus a été aidé par la découverte de pulsars en 1967, qui, en 1969, se sont révélés être en rotation rapide les étoiles à neutrons. Jusqu'à ce moment, les étoiles à neutrons, comme des trous noirs, étaient considérés comme des curiosités simplement théoriques; mais la découverte des pulsars montré leur pertinence physique et stimulé un intérêt supplémentaire dans tous les types d'objets compacts qui pourraient être formés par effondrement gravitationnel.
En cette période des solutions plus générales de trous noirs ont été trouvés. En 1963, Roy Kerr trouvé la solution exacte pour un trou noir en rotation. Deux ans plus tard, Ezra Newman a trouvé la solution de révolution pour un trou noir qui est à la fois rotatif et chargée électriquement . Grâce au travail de Werner Israel, Brandon Carter, et David Robinson du Théorème de calvitie est apparu, indiquant qu'une solution stationnaire du trou noir est complètement décrit par les trois paramètres de la Kerr-Newman métrique; masse , moment angulaire , et de charge électrique .
Au début, il a été soupçonné que les caractéristiques étranges des solutions de trous noirs étaient artefacts pathologiques des conditions de symétrie imposées, et que les singularités ne apparaît pas dans des situations génériques. Ce point de vue a eu lieu notamment en Vladimir Belinsky, Isaak Khalatnikov, et Evgeny Lifshitz, qui a essayé de prouver que aucun singularités apparaissent dans des solutions génériques. Cependant, à la fin des années 1960 Roger Penrose et Stephen Hawking a utilisé des techniques mondiaux de prouver que singularités apparaissent générique.
Les travaux de James Bardeen, Jacob Bekenstein, Carter, et Hawking dans les années 1970 ont conduit à la formulation de la thermodynamique des trous noirs. Ces lois décrivent le comportement d'un trou noir en étroite analogie avec le lois de la thermodynamique de masse relative à l'énergie, zone à l'entropie , et gravité de surface à la température . L'analogie était achevée lorsque Hawking, en 1974, a montré que la théorie quantique des champs prédit que les trous noirs devraient rayonner comme un corps noir avec une proportionnelle de température à la gravité du trou noir de surface.
Le terme "trou noir" a d'abord été utilisé publiquement par John Wheeler lors d'une conférence en 1967. Même se il est généralement crédité d'inventer l'expression, il a toujours insisté sur le fait qu'il lui a été suggéré par quelqu'un d'autre. La première utilisation du terme est par un journaliste Ann Ewing dans son article «« trous noirs »dans l'espace", en date du 18 Janvier 1964, qui était un rapport sur une réunion de la Association américaine pour l'avancement des sciences. Après l'utilisation de Wheeler du terme, il a été rapidement adopté en usage général.
Propriétés et la structure
Le Théorème de calvitie stipule que, dès qu'il atteint un état stable après la formation, un trou noir n'a que trois propriétés physiques indépendants: masse , de charge et moment angulaire . Les deux trous noirs qui partagent les mêmes valeurs pour ces propriétés, ou paramètres, sont indiscernables selon classiques (ce est à dire non quantique ) mécanique.
Ces propriétés sont spéciaux parce qu'ils sont visibles de l'extérieur d'un trou noir. Par exemple, un trou noir chargé repousse autres charges comme comme tout autre objet chargé. De même, la masse totale à l'intérieur d'une sphère contenant un trou noir peut être trouvé en utilisant l'analogue gravitationnel de la loi de Gauss , le Masse ADM, loin du trou noir. De même, le moment angulaire peut être mesurée de loin loin en utilisant cadre traîner par le gravitomagnetic domaine.
Quand un objet tombe dans un trou noir, toute informations sur la forme de l'objet ou de la distribution de la charge sur elle est uniformément répartie le long de l'horizon du trou noir, et est perdu pour les observateurs extérieurs. Le comportement de l'horizon dans cette situation est une système dissipatif qui est très analogue à celle d'une membrane élastique conductrice avec friction et la résistance électrique -la paradigme de la membrane. Ceci est différent des autres théories des champs comme l'électromagnétisme, qui ne ont pas tout frottement ou de la résistivité à l'échelle microscopique, car ils sont temps réversible. Parce que un trou noir finalement atteint un état stable avec seulement trois paramètres, il ne existe aucun moyen pour éviter de perdre des informations sur les conditions initiales: les champs gravitationnels et électriques d'un trou noir donnent très peu d'informations sur ce qui se passait dans l'information qui est perdu. comprend toute quantité qui ne peut pas être mesurée loin de l'horizon du trou noir, y compris environ conservé nombres quantiques tels que le total nombre baryonique et Numéro lepton. Ce comportement est si déconcertant qu'il a été appelé le trou noir perte d'information de paradoxe.
Propriétés physiques
Les simples trous noirs ont une masse mais ni charge électrique, ni de moment angulaire. Ces trous noirs sont souvent désignés comme Schwarzschild trous noirs après Karl Schwarzschild qui a découvert cette solution en 1916. Selon Le théorème de Birkhoff, ce est le seul solution de vide qui est à symétrie sphérique. Cela signifie qu'il n'y a pas de différence observable entre le champ gravitationnel d'un tel trou noir et celle de tout autre objet sphérique de même masse. La notion populaire d'un trou noir "aspirer tout" dans ses environs ne est correcte près de l'horizon d'un trou noir; loin, le champ gravitationnel externe est identique à celle de tout autre organisme de la même masse.
Solutions décrivant les trous noirs plus généraux existent également. Trous noirs chargés sont décrits par la Reissner-Nordström métrique, tandis que le Métrique de Kerr décrit un trou noir en rotation. La plus générale solution stationnaire trou noir connu est le Trou noir de Kerr-Newman, qui décrit un trou noir à la fois la charge et de moment angulaire.
Alors que la masse d'un trou noir peut prendre ne importe quelle valeur positive, la charge et le moment cinétique sont limités par la masse. En Unités de Planck, la charge électrique Q totale et le moment cinétique J global devraient satisfaire
pour un trou noir de masse M. Les trous noirs saturant cette inégalité sont appelés extrémal. Solutions des équations d'Einstein qui violent cette inégalité existent, mais ils ne possèdent pas un horizon des événements. Ces solutions ont dite singularités nues qui peuvent être observés de l'extérieur, et sont donc considérés comme non physique. Le Censure cosmique exclut la formation de ces singularités, quand ils sont créés par l'effondrement gravitationnel d' question réaliste. Cela est confirmé par des simulations numériques.
En raison de la relativement grande force de la force électromagnétique , les trous noirs formant de l'effondrement des étoiles devraient conserver la charge presque neutre de l'étoile. Rotation, cependant, devrait être une caractéristique commune des objets compacts. Le candidat trou noir binaire source de rayons X GRS 1915 + 105 semble avoir un moment angulaire proche de la valeur maximale autorisée.
| Classe | Masse | Taille |
|---|---|---|
| Un trou noir supermassif | ~ 10 5 -10 9 M Sun | ~ 0,001 à 10 UA |
| Trou noir de masse intermédiaire | ~ 10 3 M Sun | 10 ~ 3 km ≈ R Terre |
| Trou noir stellaire | ~ 10 M Sun | ~ 30 km |
| Micro trou noir | jusqu'à ~ M Lune | jusqu'à ~ 0,1 mm |
Les trous noirs sont généralement classés en fonction de leur masse, indépendante de l'élan angulaire J ou électrique charge Q. La taille d'un trou noir, tel que déterminé par le rayon de l'horizon des événements, ou Rayon de Schwarzschild, est à peu près proportionnelle à la masse M par
où r sh est le rayon de Schwarzschild et M est le Sun masse du Soleil Cette relation ne est exacte que pour les trous noirs avec une charge nulle et le moment cinétique; pour plus de trous noirs générale, on peut différer d'un facteur de deux.
Event horizon
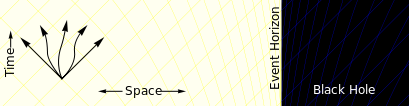 Loin du trou noir une particule peut se déplacer dans ne importe quelle direction, comme illustré par l'ensemble des flèches. Il est seulement limité par la vitesse de la lumière. |
 Plus près du trou noir l'espace-temps commence à se déformer. Il ya plusieurs chemins qui vont vers le trou noir de chemins qui se éloignent. |
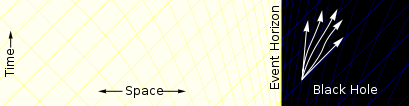 A l'intérieur de l'horizon des événements tous les chemins mettre la particule plus près du centre du trou noir. Il ne est plus possible de la particule de se échapper. |
La caractéristique d'un trou noir est l'apparition d'un événement horizon une limite dans l'espace-temps à travers laquelle la matière et la lumière ne peut passer vers l'intérieur vers la masse du trou noir. Rien, pas même la lumière, ne peut échapper à l'intérieur de l'horizon des événements. L'horizon d'événement est appelé en tant que telle parce que si un événement se produit dans les limites, les informations de cet événement ne peut pas atteindre un observateur extérieur, ce qui rend impossible de déterminer si un tel événement se est produit.
Comme prédit par la relativité générale, la présence d'une masse déforme l'espace-temps de manière à ce que les chemins empruntés par les particules pli vers la masse. A l'horizon d'événement d'un trou noir, cette déformation devient si forte qu'il n'y a pas chemins qui mènent loin du trou noir.
Pour un observateur distant, horloges à proximité d'un trou noir semblent cocher plus lentement que ceux qui sont plus loin du trou noir. En raison de cet effet, connu sous le nom gravitationnelle dilatation du temps, un objet tombant dans un trou noir semble ralentir à l'approche de l'horizon des événements, prenant un temps infini pour l'atteindre. Dans le même temps, tous les processus sur cet objet ralentissent, pour un observateur extérieur fixe, provoquant la lumière émise apparaisse plus rouge et le gradateur, un effet connu comme redshift gravitationnel. Finalement, à un point juste avant qu'il ne atteigne l'horizon des événements, l'objet qui tombe devient si faible qu'il ne peut plus être vu.
D'autre part, un observateur de tomber dans un trou noir ne remarque pas un de ces effets comme il traverse l'horizon des événements. Selon sa propre horloge, il traverse l'horizon d'événements après un temps fini sans noter tout comportement singulier. En particulier, il est incapable de déterminer exactement quand il le traverse, comme il est impossible de déterminer l'emplacement de l'horizon des événements à partir d'observations locales.
La forme de l'horizon des événements d'un trou noir est toujours à peu près sphérique. Pour (statiques) trous noirs non rotatifs la géométrie est précisément sphérique, tandis que pour les trous noirs en rotation la sphère est un peu aplatie.
Singularité
Au centre d'un trou noir comme décrit par la relativité générale se trouve une singularité gravitationnelle, une région où la courbure de l'espace-temps devient infinie. Pour un trou noir non rotatif, cette région prend la forme d'un seul point et pour un trou noir en rotation, il est enduit pour former un singularité anneau situé dans le plan de rotation. Dans les deux cas, la région singulière a zéro volume. Il peut également être démontré que la région singulière contient toute la masse de la solution de trou noir. La région singulière peut donc être considéré comme ayant infinie densité .
Les observateurs de tomber dans un trou noir de Schwarzschild (non rotatif) et aucune accusation ne peuvent pas éviter d'être transporté dans la singularité, une fois qu'ils traversent l'horizon des événements. Ils peuvent prolonger l'expérience en accélérant loin de ralentir leur descente, mais seulement jusqu'à un certain point; après avoir atteint une certaine vitesse idéale, il est préférable de chute libre le reste de la manière. Quand ils atteignent la singularité, ils sont écrasés à la densité infinie et leur masse est ajouté au total du trou noir. Avant que cela arrive, ils ont été déchirées par la culture les forces de marée dans un processus parfois appelés Spaghettification ou l '«effet de nouilles».
Dans le cas d'une charge (Reissner-Nordström) ou en rotation (Kerr) trou noir, il est possible d'éviter la singularité. L'extension de ces solutions autant que possible révèle la possibilité hypothétique de sortir du trou noir dans un espace-temps différent avec le trou noir comme un acteur trou de ver. La possibilité de voyager dans un autre univers ne est cependant que théorique, car toute perturbation va détruire cette possibilité. Il semble également possible de suivre courbes de type temps fermées (remontant à son propre passé) autour de la singularité Kerr, qui conduisent à des problèmes avec la causalité comme le grand-père paradoxe. Il est prévu qu'aucun de ces effets particuliers serait survivre dans un traitement quantique correcte de rotation et des trous noirs chargés.
L'apparition de singularités dans la relativité générale est communément perçu comme signalant la répartition de la théorie. Cette répartition, cependant, est prévu; il se produit dans une situation où les effets quantiques devraient décrire ces actions en raison de la densité extrêmement élevée et par conséquent, des interactions de particules. À ce jour, il n'a pas été possible de combiner quantique et effets gravitationnels dans une seule théorie, bien qu'il existe des tentatives pour formuler une telle théorie de la gravité quantique. On se attend généralement qu'une telle théorie ne figurera pas des singularités.
sphère de Photon
La sphère de photons est une limite sphérique d'épaisseur nulle de telle sorte que les photons se déplaçant le long des tangentes à la sphère sera pris au piège dans une orbite circulaire. Pour les non-trous noirs en rotation, la sphère de photons a un rayon de 1,5 fois le rayon de Schwarzschild. Les orbites sont dynamiquement instable, donc toute petite perturbation (comme une particule de matière infalling) va croître au fil du temps, soit la mise sur une trajectoire vers l'extérieur se échapper du trou noir ou une spirale vers l'intérieur de franchir finalement l'horizon des événements.
Tandis que la lumière peut encore échapper à l'intérieur de la sphère des photons, toute la lumière qui traverse la sphère des photons sur une trajectoire entrant sera capturée par le trou noir. Ainsi, toute lumière atteignant un observateur extérieur à partir de l'intérieur de la sphère des photons doit avoir été émis par des objets à l'intérieur de la sphère de photons mais toujours en dehors de l'horizon des événements.
Autre objets compacts, tels que les étoiles à neutrons, peuvent aussi avoir des sphères de photons. Cela découle du fait que le champ gravitationnel d'un objet ne dépend pas de sa taille réelle, donc ne importe quel objet qui est plus petit que 1,5 fois le rayon de Schwarzschild correspondant à sa masse sera en effet avoir une sphère des photons.
Ergosphère

Trous noirs en rotation sont entourés par une région de l'espace-temps dans lequel il est impossible de rester immobile, appelé le ergosphère. Ce est le résultat d'un processus connu sous le nom frame-glisser; relativité générale prédit que toute masse en rotation aura tendance à «glisser» légèrement le long de la l'espace-temps qui l'entoure immédiatement. Tout objet près de la masse en rotation aura tendance à commencer à bouger dans le sens de rotation. Pour un trou noir en rotation, cet effet devient si forte près de l'horizon d'événement qu'un objet devrait se déplacer plus vite que la vitesse de la lumière dans la direction opposée à juste rester immobile.
Le ergosphère d'un trou noir est délimitée par la (externe) horizon des événements à l'intérieur et un sphéroïde aplati, qui coïncide avec l'horizon des événements aux pôles et est sensiblement plus large autour de l'équateur. La limite extérieure est parfois appelé le ergosurface.
Objets et rayonnement peuvent échapper normalement du ergosphère. À travers le Processus de Penrose, objets peut sortir de la ergosphère avec plus d'énergie qu'ils sont entrés. Cette énergie provient de l'énergie du trou noir en rotation l'amenant à se ralentir.
Formation et évolution
Compte tenu de la nature exotique des trous noirs, il peut être naturelle à se demander si ces objets bizarres pourraient exister dans la nature ou de suggérer qu'ils ne sont que des solutions pathologiques à des équations d'Einstein. Einstein lui-même pensait à tort que les trous noirs ne feraient pas, parce qu'il a jugé que le moment angulaire de particules effondrement se stabiliserait leur mouvement à un rayon. Cela a conduit la communauté de la relativité générale de rejeter tous les résultats contraires pendant de nombreuses années. Cependant, une minorité de relativistes a continué à soutenir que les trous noirs sont des objets physiques, et à la fin des années 1960, ils avaient persuadé la majorité des chercheurs dans le domaine qu'il n'y a aucun obstacle à la formation d'un horizon des événements.
Une fois que se forme un horizon d'événement, Penrose a prouvé que une singularité formera quelque part à l'intérieur. Peu de temps après, Hawking a montré que de nombreuses solutions cosmologiques décrivant le Big Bang ont singularités sans champs scalaires ou autres matières exotiques (voir Penrose-Hawking Les théorèmes de singularité). Le Solution Kerr, le Théorème de calvitie et les lois de la thermodynamique des trous noirs ont montré que les propriétés physiques des trous noirs étaient simple et compréhensible, ce qui les rend sujets respectables pour la recherche. Le processus de formation principal pour les trous noirs devrait être le effondrement gravitationnel d'objets lourds tels que des étoiles, mais il ya aussi des processus plus exotiques qui peuvent conduire à la production de trous noirs.
Effondrement gravitationnel
Effondrement gravitationnel se produit lorsqu'un objet INTERNE la pression est insuffisante pour résister propre gravité de l'objet. Pour les étoiles cela se produit généralement soit parce qu'une étoile a trop peu de «carburant» à gauche pour maintenir sa température à travers nucléosynthèse stellaire, ou parce qu'une étoile qui aurait été stable reçoit la matière supplémentaire dans une manière qui ne soulève pas de sa température de base. Dans les deux cas la température de l'étoile ne est plus suffisamment élevé pour empêcher de se effondrer sous son propre poids. L'effondrement peut être arrêté par la pression de dégénérescence des mandants de l'étoile, la question de condensation dans un exotique état plus dense. Le résultat est l'un des divers types de étoile compacte. Le type d'étoile compacte formée dépend de la masse du résidu-la question qui reste après les couches extérieures ont été emportés, comme d'une supernova explosion ou par des pulsations menant à une nébuleuse planétaire . Notez que cette masse peut être sensiblement moins que les étoiles-restes initiales de plus de 5 masses solaires sont produites par des étoiles qui étaient plus de 20 masses solaires avant l'effondrement.
Si la masse du résidu dépasse environ 3-4 masses solaires (la Limite d'Oppenheimer-Volkoff) -soit parce que l'étoile d'origine était très lourd, soit parce que le reste a recueilli une masse supplémentaire par accrétion de matière-même la pression de dégénérescence des neutrons est insuffisante pour arrêter l'effondrement. Aucun mécanisme connu (sauf la pression de dégénérescence éventuellement quark, voir quark étoiles) est assez puissant pour arrêter l'implosion et l'objet va inévitablement se effondrer pour former un trou noir.
La chute gravitationnelle des étoiles lourds est supposé être responsable de la formation de trous noirs de masse stellaire. La formation d'étoiles dans l'univers primitif peut avoir entraîné étoiles très massives, qui, après leur effondrement aurait produites trous noirs de 3 jusqu'à 10 masses solaires. Ces trous noirs pourraient être les graines des trous noirs supermassifs trouvés dans les centres de la plupart des galaxies.
Alors que la plupart de l'énergie libérée lors de l'effondrement gravitationnel est émise très rapidement, un observateur extérieur ne voit pas vraiment la fin de ce processus. Même si l'effondrement prend un temps fini de la cadre de la matière infalling de référence, un observateur distant voit le matériau infalling lente et arrêter juste au-dessus de l'horizon de l'événement, en raison de gravitationnelle dilatation du temps. Lumière de la matière se effondrer prend plus de temps et plus de temps à atteindre l'observateur, à la lumière émise juste avant les formes d'horizon d'événement est retardé d'un temps infini. Ainsi l'observateur extérieur ne voit jamais la formation de l'horizon des événements; à la place, le matériau se effondrer semble devenir de plus en plus d'intensité et décalée vers le rouge, éventuellement se estomper.
Trous noirs primordiaux dans le Big Bang
Effondrement gravitationnel nécessite une grande densité. Dans l'époque actuelle de l'univers ces fortes densités ne se trouvent que dans les étoiles, mais dans l'univers primitif peu de temps après les Big Bang densités étaient beaucoup plus grande, permettant éventuellement à la création de trous noirs. La haute densité ne est pas suffisant pour permettre la formation de trous noirs depuis une distribution de masse uniforme ne permettra pas la masse à tasser. Dans le but de trous noirs primordiaux pour former dans un tel milieu dense, il doit y avoir perturbations de densité initiales qui peuvent ensuite se développer sous leur propre gravité. Différents modèles pour l'univers primitif varient largement dans leurs prédictions de la taille de ces perturbations. Différents modèles prévoient la création de trous noirs, allant d'une Masse de Planck à des centaines de milliers de masses solaires. Trous noirs primordiaux pourraient ainsi tenir compte de la création de tout type de trou noir.
Collisions à haute énergie

Effondrement gravitationnel ne est pas le seul processus qui pourraient créer des trous noirs. En principe, les trous noirs pourraient être formés dans de haute énergie collisions qui permettent d'atteindre une densité suffisante. En 2002, aucun de ces événements ont été détectés, soit directement, soit indirectement, comme une déficience de l'équilibre de masse dans expériences de l'accélérateur de particules. Cela donne à penser qu'il doit y avoir une limite inférieure pour la masse des trous noirs. Théoriquement, cette limite devrait se situer autour de la Masse de Planck (m P = √ ± c / ≈ 1,2 G × 10 19 GeV / c 2 ≈ 2,2 × 10 -8 kg), où sont attendus les effets quantiques pour invalider les prédictions de la relativité générale. Cela mettrait la création de trous noirs fermement hors de la portée de tout processus de haute énergie se produisant sur ou près de la Terre. Toutefois, certains développements dans la gravité quantique suggèrent que la masse de Planck pourrait être beaucoup plus faible: certains braneworld scénarios par exemple mis la frontière aussi bas que 1 TeV / c 2. Il serait ainsi envisageable pour micros trous noirs à être créés dans les collisions à haute énergie se produisent quand les rayons cosmiques frappent l'atmosphère de la Terre, ou éventuellement dans le nouveau Large Hadron Collider CERN. Pourtant, ces théories sont très spéculative, et la création de trous noirs dans ces processus est jugée peu probable par de nombreux spécialistes. Même si des micro trous noirs devraient être formés dans ces collisions, il est prévu qu'ils se évaporer dans environ 10 -25 secondes, posant aucune menace pour la Terre.
Croissance
Une fois un trou noir se est formé, il peut continuer à croître en absorbant la matière supplémentaire. Tout trou noir continuellement absorber gaz et poussière interstellaire de ses environs directs et omniprésente rayonnement de fond cosmologique. Ce est le principal processus par lequel les trous noirs supermassifs semblent avoir augmenté. Un processus similaire a été suggérée pour la formation de trous noirs de masse intermédiaire dans les amas globulaires .
Une autre possibilité est d'un trou noir de fusionner avec d'autres objets tels que des étoiles ou même d'autres trous noirs. Ce est pensé pour avoir été important, surtout pour le développement précoce de trous noirs supermassifs, qui aurait formé de la coagulation de nombreux petits objets. Le processus a également été proposé que l'origine de certaines intermédiaire trous noirs de masse.
Évaporation
En 1974, Hawking a montré que les trous noirs ne sont pas entièrement noir, mais émettent de petites quantités de rayonnement thermique; un effet qui est devenu connu comme le rayonnement de Hawking . En appliquant la théorie quantique des champs à une statique fond de trou noir, il a déterminé qu'un trou noir devrait émettre des particules dans une parfaite noir spectre du corps. Depuis la publication de Hawking, beaucoup d'autres ont vérifié le résultat par différentes approches. Si la théorie de Hawking de rayonnement du trou noir est correcte, alors les trous noirs devraient diminuer au fil du temps et évaporer parce qu'ils perdent de la masse par l'émission de photons et autres particules. La température de ce spectre thermique ( température Hawking ) est proportionnelle à la gravité de surface du trou noir, qui, pour un trou noir de Schwarzschild, est inversement proportionnelle à la masse. Ainsi, de grands trous noirs émettent moins de radiations que les petits trous noirs.
Un trou noir stellaire d'une masse solaire a une température d'environ 100 Hawking nanokelvins. Cela est beaucoup moins que la température de 2,7 K fond diffus cosmologique rayonnement. Trous noirs de masse stellaire ou plus reçoivent plus de masse à partir du fond diffus cosmologique qu'ils émettent par rayonnement Hawking et donc va croître au lieu de psy. Pour avoir une température supérieure à 2.7 Hawking K (et être capable de s'évaporer), un trou noir doit avoir moins de masse que la Lune . Un tel trou noir aurait un diamètre de moins d'un dixième de millimètre.
Si un trou noir est très faible sont attendus les effets des rayonnements à devenir très fort. Même un trou noir qui est lourd par rapport à un être humain serait s'évaporer en un instant. Un trou noir le poids d'une voiture aurait un diamètre d'environ 10 -24 m et prendre une nanoseconde pour évaporer, période pendant laquelle il aurait brièvement une luminosité plus de 200 fois celle du Soleil Trous noirs de faible masse sont attendus pour évaporer encore plus vite; par exemple, un trou noir de masse 1 TeV / c 2 prendrait moins de 10 -88 secondes pour faire évaporer complètement. Pour un si petit trou noir, sont attendus les effets de la gravitation quantique à jouer un rôle important et pourrait même-bien que les développements actuels dans la gravité quantique ne signifie pas que l'on hypothétiquement faire un si petit trou noir stable.
Les données d'observation
Par leur nature même, les trous noirs ne émettent pas directement tous les signaux autres que le rayonnement de Hawking hypothétique; puisque le rayonnement de Hawking pour un trou noir astrophysique est prévu pour être très faible, ce qui rend impossible de détecter directement astrophysiques trous noirs de la Terre. Une exception possible à la radiation Hawking étant faible est la dernière étape de l'évaporation de la lumière (primordiaux) trous noirs; Recherches pour de tels éclairs, dans le passé ont échoué et fournir des limites strictes sur la possibilité de l'existence de trous noirs primordiaux lumière. NASA Fermi Gamma-ray Space Telescope lancé en 2008 se poursuivra la recherche de ces éclairs.
Les astrophysiciens à la recherche de trous noirs ont donc compter sur des observations indirectes. L'existence d'un trou noir peut parfois être déduite en observant ses interactions gravitationnelles avec son environnement. Un projet dirigé par le MIT Haystack Observatory tente d'observer l'horizon d'événement d'un trou noir directement. Les premiers résultats sont encourageants.
Accrétion de matière
En raison de la conservation du moment angulaire , le gaz de tomber dans le gravitationnel ainsi créé par un objet massif typiquement former une structure en forme de disque autour de l'objet. Frottement à l'intérieur du disque provoque moment angulaire d'être transporté vers l'extérieur, permettant question à tomber davantage vers l'intérieur, en libérant l'énergie potentielle et l'augmentation de la température du gaz. Dans le cas de objets compacts comme des naines blanches , étoiles à neutrons et les trous noirs, le gaz dans les régions intérieures devient tellement chaude qu'elle émet de grandes quantités de rayonnement (principalement des rayons X), qui peut être détecté par les télescopes. Ce processus d'accrétion est l'un des processus de production d'énergie les plus efficaces connus; jusqu'à 40% de la masse au repos de la matière accumulée peut être émis en rayonnement. (Dans la fusion nucléaire seulement environ 0,7% de la masse reste sera émis sous forme d'énergie.) Dans de nombreux cas, disques d'accrétion sont accompagnés de jets relativistes émis le long des poteaux, qui emportent beaucoup de l'énergie. Le mécanisme de la création de ces jets est actuellement mal comprise.
En tant que tel nombre de phénomènes plus énergiques de l'univers ont été attribués à l'accrétion de matière sur les trous noirs. En particulier, noyaux actifs de galaxies et quasars sont soupçonnés d'être les disques d'accrétion des trous noirs supermassifs. De même, binaires X sont généralement acceptées pour être étoiles binaires systèmes dans lesquels l'un des deux étoiles est un objet compact accrétion question de son compagnon. Il a également été suggéré que certaines sources de rayons X ultralumineuses peuvent être les disques d'accrétion de trous noirs de masse intermédiaire.
Binaires X
Binaires X sont étoiles binaires systèmes qui sont lumineuse dans la partie X-ray du spectre. Ces émissions de rayons X sont généralement pensés pour être causé par l'une des stars de composants étant une question objet compact accrétion de l'autre étoile (régulière). La présence d'une étoile ordinaire dans un tel système offre une occasion unique pour l'étude de l'objet central et déterminer si elle pourrait être un trou noir.
Si un tel système émet des signaux qui peuvent être directement remonter à l'objet compact, il ne peut pas être un trou noir. L'absence d'un tel signal ne cependant pas exclure la possibilité que l'objet compact est une étoile à neutrons. En étudiant l'étoile compagnon, il est souvent possible d'obtenir les paramètres de l'orbite du système et d'obtenir une estimation de la masse de l'objet compact. Si cela est beaucoup plus grande que la limite Tolman-Oppenheimer-Volkoff (qui est, la masse maximale d'une étoile à neutrons peut avoir avant de se effondrer) alors l'objet ne peut pas être une étoile à neutrons et est généralement prévu pour être un trou noir.
Le premier candidat pour un trou noir, Cygnus X-1, a été découvert dans cette façon par Charles Thomas Bolton, Louise Webster et Paul Murdin en 1972. Certains de doute, cependant, est resté en raison des incertitudes résultant de l'étoile compagnon étant beaucoup plus lourd que le trou noir de candidat. Actuellement, de meilleurs candidats pour les trous noirs se trouvent dans une classe de binaires X dits mous transitoires X-ray. Dans cette classe de système l'étoile compagnon est relativement faible masse permettant des estimations plus précises de la masse du trou noir. En outre, ces systèmes ne sont actives que dans les rayons X pendant plusieurs mois une fois tous les 10-50 ans. Au cours de la période de faible émission de rayons X (appelée quiescence), le disque d'accrétion est extrêmement faible permettant une observation détaillée de l'étoile compagnon au cours de cette période. Une des meilleures de ces candidats est v404 Cyg.
Quiescence et le flux d'accrétion advection dominé
La faiblesse du disque d'accrétion au cours quiescence est soupçonnée d'être causées par le flux entrant dans un mode appelé un flux d'accrétion advection-dominé (ADAF). Dans ce mode, presque toute l'énergie produite par le frottement sur le disque est balayé avec le flux au lieu d'rayonnée loin. Si ce modèle est correct, alors il fait preuve qualitative solide pour la présence d'un horizon des événements. Parce que, si l'objet au centre du disque avait une surface solide, il serait émettent de grandes quantités de rayonnement que le gaz très énergique frappe la surface, un effet qui est observée pour les étoiles à neutrons dans un état similaire.
Oscillations quasi-périodiques
L'émission de rayons X à partir de disques d'accrétion scintille parfois à certaines fréquences. Ces signaux sont appelés oscillations quasi-périodiques et sont censés être causée par un matériau se déplaçant le long du bord intérieur du disque d'accumulation (l'orbite circulaire stable la plus interne). En tant que tels leur fréquence est liée à la masse de l'objet compact. Ils peuvent donc être utilisés comme une alternative pour déterminer la masse des trous noirs potentiels.
Noyaux galactiques
Les astronomes utilisent le terme " de galaxie active »pour décrire les galaxies avec des caractéristiques inhabituelles, comme inhabituelle émission de la raie spectrale et l'émission de radio très forte. Les études théoriques et observationnelles ont montré que l'activité dans ces noyaux actifs de galaxies (AGN) peut être expliquée par la présence de trous noirs supermassifs. Les modèles de ces AGN sont constitués d'un trou noir central qui peut être des millions ou des milliards de fois plus massives que le Soleil ; un disque de gaz et de poussière appelé un disque d'accrétion; et deux jets qui sont perpendiculaires au disque d'accrétion.
Bien que les trous noirs supermassifs sont censés être trouvé dans la plupart AGN, les noyaux de galaxies seulement certains ont été plus soigneusement étudiée dans des tentatives à la fois d'identifier et de mesurer les masses réelles des candidats supermassifs de trou noir central. Certains des galaxies les plus notables avec supermassifs candidats trous noirs comprennent la galaxie d'Andromède , M32, M87, NGC 3115, NGC 3377, NGC 4258, et la galaxie du Sombrero.
Il est maintenant largement admis que le centre de presque toutes les galaxies, et pas seulement les actifs, contient un trou noir supermassif. La corrélation observation étroite entre la masse de ce trou et la dispersion de vitesse de de la galaxie hôte du renflement, connu comme le rapport M-sigma, suggère fortement un lien entre la formation du trou noir et la galaxie elle-même.

Actuellement, la meilleure preuve d'un trou noir supermassif provient de l'étude de la bonne mouvement des étoiles près du centre de notre propre Voie Lactée . Depuis 1995, les astronomes ont suivi le mouvement de 90 étoiles dans une région appelée Sagittarius A *. En adaptant leur mouvement à orbites de Kepler, ils ont pu déduire en 1998 que 2,6 millions de masses solaires doivent être contenues dans un volume avec un rayon de 0,02 années-lumière. Depuis lors, l'une des stars-disant S2-a complété une orbite complète. D'après les données orbitale ils étaient en mesure de placer de meilleurs contraintes sur la masse et la taille de l'objet causant le mouvement orbital d'étoiles dans le Sagittarius A * de la région, estimant qu'il ya une masse sphérique de 4,3 millions de masses solaires contenue dans un rayon de moins de 0,002 années-lumière. Bien que ce soit plus de 3000 fois le rayon de Schwarzschild correspondant à cette masse, il est au moins compatible avec l'objet central étant un trou noir supermassif, et aucun "pôle réaliste [des étoiles] est physiquement tenable".
Effets de la forte gravité
Une autre façon que la nature du trou noir d'un objet peut être testé à l'avenir est à travers l'observation des effets causés par la forte gravité dans leur voisinage. Un tel effet est lentille gravitationnelle: La déformation de l'espace-temps autour d'un objet massif provoque rayons lumineux déviés peu comme la lumière passant à travers une optique lentille. Les observations ont été faites de la faiblesse de lentille gravitationnelle, dans lequel les rayons lumineux sont déviés par seulement quelques-uns secondes d'arc. Cependant, il n'a jamais été directement observée pour un trou noir. Une possibilité pour l'observation de lentille gravitationnelle par un trou noir serait d'observer les étoiles en orbite autour du trou noir. Il ya plusieurs candidats pour une telle observation en orbite autour de Sagittarius A *.
Une autre option serait l'observation directe des ondes gravitationnelles produites par un objet tombant dans un trou noir, par exemple un objet compact tomber dans un trou noir supermassif par un rapport de masse Inspiral extrême. Correspondant à la forme d'onde observée aux prédictions de la relativité générale permettrait des mesures de précision de la masse et du moment angulaire de l'objet central, tandis que dans le même temps à tester la relativité générale. Ces types d'événements sont une cible primaire pour le projet Laser Interferometer Space Antenna.
Alternatives
La preuve pour les trous noirs stellaires repose fortement sur l'existence d'une limite supérieure pour la masse d'une étoile à neutrons. La taille de cette limite dépend fortement des hypothèses faites sur les propriétés de la matière dense. Nouveaux exotiques phases de la matière pourraient pousser jusqu'à cette borne. Une phase de libres quarks à haute densité pourrait permettre l'existence de denses étoiles de quarks, et certains modèles supersymétriques prédire l'existence de Q étoiles. Certaines extensions du modèle standard postulent l'existence de preons que blocs de construction fondamentaux des quarks et des leptons, qui pourrait hypothétiquement former étoiles Preon. Ces modèles hypothétiques pourraient expliquer un certain nombre d'observations stellaires de candidats trous noirs. Cependant, il peut être démontré à partir des arguments généraux en relativité générale que tout tel objet aura une masse maximale.
Depuis la densité moyenne d'un trou noir à l'intérieur de son rayon de Schwarzschild est inversement proportionnelle au carré de sa masse, trous noirs supermassifs sont beaucoup moins dense que les trous noirs stellaires (la densité moyenne de 10 8 solaire trou noir de masse est comparable à celle de l'eau ). Par conséquent, la physique de la matière formant un trou noir supermassif est beaucoup mieux comprises et les explications alternatives possibles pour supermassifs observations de trous noirs sont beaucoup plus terre à terre. Par exemple, un trou noir supermassif pourrait être modélisé par un grand groupe d'objets très sombres. Toutefois, ces solutions de rechange ne sont généralement pas assez stable pour expliquer les supermassifs candidats trous noirs.
La preuve pour les trous noirs stellaires et supermassifs implique que, pour que les trous noirs ne pas former, la relativité générale doit échouer en tant que théorie de la gravité, peut-être en raison de l'apparition de la mécanique quantique corrections. Une caractéristique très attendu d'une théorie de la gravité quantique est qu'il ne figurera pas singularités ou horizons d'événements (et donc pas de trous noirs). Au cours des dernières années, beaucoup d'attention a été attirée par le modèle de fuzzball dans la théorie des cordes . Basé sur des calculs dans des situations spécifiques dans la théorie des cordes, la proposition suggère que génériquement les états individuels d'une solution de trou noir ne disposent pas d'un horizon ou singularité événement, mais que pour un observateur classique / semi-classique de la moyenne statistique de ces États ne semble tout comme un trou noir ordinaire en relativité générale.
Questions ouvertes
Entropie et de la thermodynamique

En 1971, Hawking a montré dans des conditions générales que la superficie totale des horizons d'événements de toute collection de trous noirs classiques ne peut jamais diminuer, même si elles entrent en collision et fusionnent. Ce résultat, maintenant connu comme le deuxième loi de mécanique de trou noir, est remarquablement similaire à la deuxième loi de la thermodynamique , qui stipule que le total entropie d'un système ne peut jamais diminuer. Comme pour les objets classiques au zéro absolu de température, on a supposé que les trous noirs avaient entropie nulle. Si tel était le cas, la deuxième loi de la thermodynamique serait violé par la matière d'entropie chargé entrer dans un trou noir, résultant en une diminution de l'entropie totale de l'univers. Par conséquent, Bekenstein proposé qu'un trou noir devrait avoir une entropie, et qu'il devrait être proportionnel à sa zone d'horizon.
Le lien avec les lois de la thermodynamique a été renforcée par la découverte de Hawking que la théorie quantique des champs prédit qu'un trou noir rayonne rayonnement du corps noir à une température constante. Cela provoque apparemment une violation de la deuxième loi de la mécanique de trou noir, puisque le rayonnement emportera l'énergie du trou noir amenant à se rétrécir. Le rayonnement, porte cependant aussi loin entropie, et il peut être prouvé sous des hypothèses générales que la somme de l'entropie de la question entourant un trou noir et un quart de la superficie de l'horizon, telle que mesurée dans les unités de Planck est en fait toujours croissante. Cela permet la formulation de la première loi de mécanique de trou noir comme un analogue de la première loi de la thermodynamique , avec l'action de masse comme l'énergie, la gravité de surface que la température et la région comme l'entropie.
Une caractéristique déroutante est que l'entropie d'un trou noir évolue avec sa zone plutôt que par son volume, car l'entropie est normalement une quantité extensive qui évolue linéairement avec le volume du système. Cette propriété étrange conduit Gerard 't Hooft et Leonard Susskind de proposer la principe holographique, ce qui suggère que tout ce qui se passe dans un volume de l'espace-temps peut être décrit par des données sur la limite de ce volume.
Bien que la relativité générale peut être utilisée pour effectuer un calcul semi-classique de trou noir entropie, cette situation est théoriquement insatisfaisant. Dans la mécanique statistique , l'entropie est entendu que de compter le nombre de configurations microscopiques d'un système qui ont les mêmes qualités macroscopiques (telles que la masse , la charge, la pression, etc.). Sans une théorie satisfaisante de la gravitation quantique, on ne peut pas effectuer un tel calcul pour les trous noirs. Certains progrès ont été réalisés dans diverses approches de la gravité quantique. En 1995, Andrew Strominger et Cumrun Vafa ont montré que le comptage des micro-spécifique d'un supersymétrique trou noir dans la théorie des cordes reproduit l'entropie Bekenstein-Hawking. Depuis lors, des résultats similaires ont été rapportés pour différents trous noirs à la fois à la théorie des cordes et dans d'autres approches de la gravité quantique comme gravitation quantique à boucles.
la perte de l'information paradoxe
| Est des informations physiques perdu dans les trous noirs? |
Parce que un trou noir n'a que quelques paramètres internes, la plupart des informations à propos de la question qui est entré dans la formation du trou noir est perdu. Il n'a pas d'importance si elle est formée à partir d'ensembles ou des chaises télévision, à la fin du trou noir ne se souvient que la masse totale, charge, et du moment angulaire. Tant que les trous noirs ont été pensés pour persister à jamais cette perte d'information est pas que problématique, car l'information peut être considéré comme existant à l'intérieur du trou noir, inaccessible de l'extérieur. Cependant, les trous noirs évaporer lentement en émettant le rayonnement de Hawking . Ce rayonnement ne semble pas porter aucune information détaillée sur la substance qui a formé le trou noir, ce qui signifie que cette information semble être disparu à jamais.
Pendant longtemps, la question de savoir si l'information est vraiment perdu dans les trous noirs (le trou informations paradoxe noir) a divisé la communauté de la physique théorique (voir Thorne-Hawking-Preskill pari). En mécanique quantique, la perte de l'information correspond à la violation de la propriété vitale appelée unitarité, qui a à voir avec la conservation de la probabilité. Il a fait valoir que la perte de unitarity impliquerait également la violation de la conservation de l'énergie. Ces dernières années, la preuve a été construit qu'en effet, l'information et unitarity sont conservés dans un traitement de gravitation quantique complète du problème.


