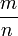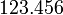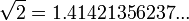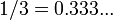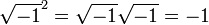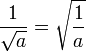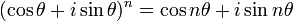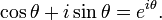Nombre

Un nombre est un objet abstrait, jetons dont sont Symboles utilisés dans comptage et mesure . Un symbole qui représente un nombre est appelé numérique, mais dans l'usage courant le nombre de mot est utilisé à la fois pour l'objet abstrait et le symbole. En plus de leur utilisation en comptage et de mesure, les chiffres sont souvent utilisés pour des étiquettes ( les numéros de téléphone), pour la commande ( numéros de série) et des codes ( ISBN). En mathématiques , la définition du nombre a été étendu au fil des ans pour inclure ces numéros que zéro , les nombres négatifs , des nombres rationnels , nombres irrationnels et nombres complexes .

Certaines procédures d'entrée un ou plusieurs numéros et la production d'un certain nombre sont appelés numérique opérations. Entrée des opérations unaire un numéro unique et la sortie d'un numéro unique. Par exemple, l'opération successeur ajoute un à un entier: le successeur de quatre est 5. sont plus fréquents opérations binaires d'entrée et de sortie deux numéros un numéro unique. Exemples d'opérations binaires comprennent outre , la soustraction , la multiplication , la division et exponentiation . L'étude des opérations numériques est appelée arithmétique .

La branche des mathématiques qui étudie les systèmes de numération abstraits tels que les groupes , anneaux et champs se appelle algèbre abstraite .

Types de numéros

Les nombres peuvent être classés en ensembles, appelés systèmes de numération . (Pour différentes méthodes d'exprimer les nombres avec des symboles, comme les chiffres romains , voir systèmes de numération .)

Nombres naturels

Les numéros les plus connus sont les nombres naturels ou des numéros de comptage: une, deux, trois, .... Certaines personnes comprennent également zéro dans les nombres naturels; Toutefois, d'autres pas.

Dans le fond de dix système numérique, en usage aujourd'hui presque universelle pour les opérations arithmétiques, les symboles des nombres naturels sont écrits en utilisant dix chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. Dans ce système de base dix, le chiffre le plus à droite d'un nombre naturel a une valeur de position de l'un, et tous les autres chiffres a une valeur de lieu dix fois celle de la valeur de position du chiffre à sa droite. Le symbole de l'ensemble des nombres naturels est N, également écrit .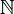

Entiers

Les nombres négatifs sont des nombres qui sont inférieurs à zéro. Ils sont à l'opposé des nombres positifs. Par exemple, si un nombre positif indique un dépôt bancaire, puis un nombre négatif indique un retrait du même montant. Les nombres négatifs sont généralement écrites en écrivant un signe négatif devant le nombre, ils sont à l'opposé de. Ainsi, à l'opposé de 7 est écrit -7. Quand le jeu des contraires des nombres naturels est combiné avec les nombres naturels et zéro, on obtient les nombres entiers Z (allemand Zahl, pluriel Zahlen), également écrites .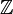

Nombres rationnels

Un nombre rationnel est un nombre qui peut être exprimée comme une fraction d'un nombre entier numérateur et un nombre entier naturel non nul dénominateur . La fraction m / n ou

représente m parties égales, où les pièces n égales de cette taille constituent un tout. Deux fractions différentes peuvent correspondre au même nombre rationnel; par exemple 1/2 et 2/4 sont égaux, à savoir:

.

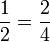Si la valeur absolue de m est supérieur à n, alors la valeur absolue de la fraction est supérieure à 1. Les fractions peut être supérieure, inférieure ou égale à 1 et peut également être positif, négatif ou nul. L'ensemble de toutes les fractions comprend les nombres entiers, puisque tout entier peut être écrit comme une fraction de dénominateur 1. Par exemple -7 peut être écrit -7/1. Le symbole pour les nombres rationnels est Q (pour quotient), également écrit .

Nombres réels

Les nombres réels comprennent tous les numéros de mesure. Les nombres réels sont généralement écrits en utilisant décimales chiffres, dans lequel un point décimal est placé à la droite de la position avec une valeur de position. Après la virgule, chaque chiffre a une valeur de position un dixième de la valeur de position du chiffre à sa gauche. Ainsi

représente une centaine, deux dizaines, trois petits, 4/10, 5/100 et 6/1000. En disant le nombre, la virgule est lu "point", ainsi: "un deux trois quatre cinq six points". Dans, par exemple, aux États-Unis et au Royaume-Uni, la décimale est représentée par un période, en Europe continentale par un virgule. Zéro est souvent écrit que 0,0 et négatifs nombres réels sont écrits avec une précédente signe moins:

.

Chaque nombre rationnel est aussi un nombre réel. Pour écrire une fraction sous forme décimale, divisez le numérateur par le dénominateur. Ce ne est pas le cas, cependant, que tout nombre réel est rationnel. Si un nombre réel ne peut pas être écrit comme une fraction de deux nombres entiers, elle est appelée irrationnelle . Une décimal qui peut être écrit comme une fraction soit extrémités (se termine) ou pour toujours répète, parce que ce est la réponse à un problème dans la division. Ainsi, le nombre réel de 0,5 peut être écrite comme 1/2 et le nombre réel de 0,333 ... (trois, jamais répétés) peut être écrit comme un tiers. D'autre part, (π du nombre réel pi ), le rapport de la circonférence de ne importe quel cercle à son diamètre , est

.

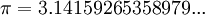Depuis la décimale ne finit jamais, ni répète, il ne peut pas être écrit comme une fraction, et est un exemple d'un nombre irrationnel. Autres nombres irrationnels comprennent

(Le racine carrée de 2, ce est le nombre positif dont le carré est 2).

Tout comme fractions peuvent être écrits dans plus d'un titre, le peuvent aussi décimales. Par exemple, si l'on multiplie les deux côtés de l'équation

par trois, nous découvrons que

.

Ainsi 1,0 et 0,999 ... sont deux nombres décimaux différentes représentant le nombre naturel 1. Il ya une infinité de nombreuses autres façons de représenter le numéro 1, par exemple 2/2, 3/3, 1,00, 1,000, et ainsi de suite.

Chaque nombre réel est rationnel ou irrationnel. Chaque nombre réel correspond à un point sur la numéro de ligne. Les nombres réels ont aussi une propriété importante, mais très technique appelée propriété limite supérieure moins. Le symbole pour les nombres réels est R ou .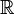

Quand un nombre réel représente une mesure , il ya toujours une marge d'erreur . Ce est souvent indiquée par arrondis ou tronquer un nombre décimal, de sorte que les chiffres qui suggèrent une plus grande précision que la mesure se sont retirés. Les chiffres restants se appellent les chiffres significatifs. Par exemple, les mesures avec une règle peuvent rarement être effectués sans une marge d'erreur d'au moins 0,01 mètres. Si les côtés d'un rectangle sont mesurés que 1,23 mètres et 4,56 mètres, puis la multiplication donne un espace pour le rectangle de 5,6088 mètres carrés. Étant donné que seuls les deux premiers chiffres après la virgule sont importants, ce est souvent arrondie à 5,61.

En algèbre abstraite , les chiffres réels sont caractérisés unique en étant le seul complètement ordonné domaine. Ils ne sont pas, cependant, un corps algébriquement clos.

Les nombres complexes

Le passage à un plus grand niveau d'abstraction, les nombres réels peuvent être étendus aux nombres complexes . Cette série de chiffres se leva, historiquement, de la question de savoir si un nombre négatif peut avoir une racine carrée . Cela a conduit à l'invention d'un nouveau numéro: la racine carrée d'un négatif, désigné par i , un symbole attribué par Leonhard Euler , et a appelé l' unité imaginaire . Les nombres complexes sont constitués de tous les nombres de la forme

où a et b sont des nombres réels. Dans l'expression a + bi, le nombre réel a est appelé la partie réelle et bi est appelé la partie imaginaire. Si la partie réelle d'un nombre complexe est égal à zéro, alors le nombre est appelé ou nombre imaginaire est désigné comme purement imaginaire; si la partie imaginaire est nul, alors le nombre est un nombre réel. Ainsi, les nombres réels sont un sous-ensemble des nombres complexes. Si les parties réelle et imaginaire d'un nombre complexe sont tous deux des nombres entiers, le nombre est appelé Nombre entier de Gauss. Le symbole pour les nombres complexes est C ou .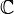

En résumé algèbre , les nombres complexes sont un exemple d'un corps algébriquement clos, ce qui signifie que chaque polynôme avec le complexe coefficients peuvent être pris en compte dans les facteurs linéaires. Comme le système de nombre réel, le système numérique est un complexe terrain et est compléter, mais contrairement aux vrais chiffres, il ne est pas ordonnée. Autrement dit, il n'y a aucun sens à dire que i est supérieur à 1, il ne existe aucune signification en disant que que i est inférieur à 1. En termes techniques, les nombres complexes ne ont pas la propriété trichotomie .

Les nombres complexes correspondent à des points sur le plan complexe , parfois appelé le plan d'Argand.

Chacun des systèmes numériques mentionnées ci-dessus est un sous-ensemble approprié de l'autre système de numération. Symboliquement, N ⊂ Z ⊂ Q ⊂ R ⊂ C.

D'autres types

Superreal, hyperréaliste et numéros surréalistes se étendent les nombres réels en ajoutant infiniment petits nombres et infiniment grand nombre, mais forment encore domaines.

L'idée derrière p-adique chiffres est la suivante: Bien que les chiffres réels peuvent avoir infiniment longues expansions à la droite de la virgule, ces chiffres permettre infiniment longues expansions vers la gauche. Le système de numérotation qui résulte dépend de ce que base est utilisée pour les chiffres: ne importe quelle base est possible, mais un système avec les meilleures propriétés mathématiques est obtenue lorsque la base est un nombre premier .

Pour le traitement des collections infinies, les nombres naturels ont été généralisées pour les nombres ordinaux et les nombres cardinaux . Le premier donne l'ordre de la collection, tandis que la seconde donne sa taille. Pour l'ensemble fini, les numéros de ordinales et cardinales sont équivalents, mais ils diffèrent dans le cas infini.

Il ya aussi d'autres ensembles de nombres avec des utilisations spécialisées. Certains sont sous-ensembles des nombres complexes. Par exemple, nombres algébriques sont les racines de polynômes avec rationnelle coefficients. Les nombres complexes qui ne sont pas algébriques sont appelés nombres transcendants.

Séries de chiffres qui ne sont pas des sous-ensembles des nombres complexes sont parfois appelés numéros hypercomplexes. Ils comprennent le quaternions H, inventé par Sir William Rowan Hamilton, dans lequel multiplication ne est pas commutative , et de la octonions, dans lequel la multiplication ne est pas associative . Éléments de domaines de la non-nulle fonction se comportent caractéristique à certains égards comme des numéros et sont souvent considérés comme les numéros par les théoriciens des nombres.

Chiffres

Numéros doivent être distingués des les chiffres, les symboles utilisés pour représenter des nombres. Le nombre cinq peut être représenté par dix fois la base chiffre «5» et par le chiffre romain "V". Notations utilisées pour représenter les nombres sont abordées dans l'article systèmes de numération . Un développement important dans l'histoire de chiffres a été le développement d'un système de positionnement, comme décimales modernes, qui peuvent représenter un très grand nombre. Les chiffres romains exigent symboles supplémentaires pour un plus grand nombre.

Histoire

Histoire de entiers

Les premiers nombres

Il est spéculé que la première utilisation connue de numéros remonte aux alentours de 30 000 BC, les os ou d'autres objets ont été découverts avec des marques coupés en eux qui sont souvent considérés marques de pointage. L'utilisation de ces marques de pointage ont été suggérées à être quelque chose de compter le temps écoulé, comme le nombre de jours, ou la tenue de registres des montants.

Systèmes de dépouillement ont aucune idée de la valeur de position (comme dans la notation décimale utilisée actuellement), ce qui limite sa représentation des grands nombres et en tant que telle est souvent considéré que ce est le premier type de système abstrait qui serait utilisée, et pourrait être considéré comme un Système numérique.

Le premier système connu avec de valeur de l'est Mésopotamienne système en base 60 (ca. 3400 BC) et le système de base connue plus tôt 10 dates pour 3100 avant JC en Egypte .

Histoire de zéro

L'utilisation de zéro comme un certain nombre doit être distingué de son utilisation comme un chiffre d'espace réservé dans place des systèmes de valeur. Beaucoup de textes indiens anciens utilisent un sanscrit mot Shunya de se référer à la notion de vide; dans les textes de mathématiques ce mot serait souvent utilisé pour désigner le nombre zéro. . Dans la même veine, Pāṇini ( 5ème siècle avant JC) a utilisé le nul (zéro) opérateur (soit un production lambda) dans la Ashtadhyayi, son grammaire algébrique pour le sanscrit langue. (Voir aussi Pingala)

Les dossiers montrent que les Grecs de l'Antiquité semblait incertain au sujet de l'état de zéro comme un nombre: ils se demandaient «comment peut« rien »quelque chose?" conduisant à intéressante philosophique et, par la période médiévale, des arguments religieux sur la nature et l'existence de zéro et le vide. Le paradoxes de Zénon d'Elée dépend en grande partie sur l'interprétation incertaine de zéro. (Les anciens Grecs même demandé si une était un nombre.)

La fin des olmèques gens du centre-sud du Mexique ont commencé à utiliser un vrai zéro (un glyphe de coquille) dans le Nouveau Monde éventuellement par le 4ème siècle avant JC, mais certainement par 40 BC, qui est devenu une partie intégrante de Numération maya et la Calendrier maya, mais n'a pas influencé anciens systèmes de numération monde.

Par 130, Ptolémée , influencée par Hipparque et les Babyloniens, utilisait un symbole pour zéro (un petit cercle avec une longue barre supérieure) dans un système de numération sexagésimal utilisant autrement alphabétique Chiffres grecs. Parce qu'il a été utilisé seul, et pas seulement comme un espace réservé ce, Zéro hellénistique était la première utilisation documentée d'un véritable zéro dans le Vieux Monde. En plus tard byzantines manuscrits de son Syntaxis Mathematica (Almageste), le zéro hellénistique avait transformé dans la lettre grecque omicron (sinon ce qui signifie 70).

Un autre zéro absolu a été utilisé dans les tableaux aux côtés de chiffres romains par 525 (première utilisation connue par Denys le Petit), mais comme un mot, nulla signifie rien, pas comme un symbole. Lorsque la division produit zéro comme un reste, nihil, ce qui signifie également rien, a été utilisé. Ces zéros médiévales ont été utilisés par tous les futurs médiévale computists (calculatrices de Pâques ). Une utilisation isolée de leur initiale, N, a été utilisé dans un tableau de chiffres romains par Bede ou un collègue 725, un véritable symbole zéro.

Une utilisation documentée début du zéro Brahmagupta (dans le Brahmasphutasiddhanta) remonte à 628. Il traités zéro comme un nombre et des opérations impliquant Il a discuté, y compris division. En ce moment (7ème siècle) le concept avait clairement atteint le Cambodge , et de la documentation montre l'idée se diffuse ensuite à la Chine et l' islamique monde.

Histoire des nombres négatifs

Le concept abstrait des nombres négatifs a été reconnu dès 100 BC - 50 avant JC. Les chinoise " Neuf chapitres sur l'art mathématique »(Jiu-zhang suanshu) contient méthodes pour trouver les zones de chiffres; tiges rouges ont été utilisés pour désigner positif coefficients, noir pour le négatif. Ce est la plus ancienne mention connue des nombres négatifs dans l'Est; la première référence dans un ouvrage ouest était dans le 3ème siècle en Grèce . Diophante visée à l'équivalent d'équation pour 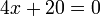(La solution serait négative) Arithmetica, en disant que l'équation a donné un résultat absurde.

Pendant le 600s, les nombres négatifs étaient en usage dans l'Inde pour représenter dettes. Référence précédente de Diophante a été discuté de façon plus explicite par le mathématicien indien Brahmagupta, dans Brahma-Sphuta-Siddhanta 628, qui a utilisé des nombres négatifs pour produire la forme générale formule quadratique qui reste en usage aujourd'hui. Toutefois, dans le 12ème siècle en Inde, Bhaskara donne racines négatives pour les équations du second degré, mais dit la valeur négative "est dans ce cas de ne pas être pris, car il est insuffisant, les gens ne approuvent pas de racines négatives."

Européennes mathématiciens, pour la plupart, ont résisté à la notion de nombres négatifs jusqu'à ce que le 17ème siècle , bien que Fibonacci permis solutions négatives dans les problèmes financiers où ils pourraient être interprétés comme des débits (chapitre 13 Liber Abaci, 1202) et plus tard comme des pertes (en Flos). Dans le même temps, les Chinois ont été indiquant les nombres négatifs en dessinant un trait diagonal par le chiffre le plus à droite du chiffre non nul du nombre positif correspondant. La première utilisation de nombres négatifs dans une œuvre européenne était par CHUQUET pendant le 15ème siècle . Il les utilise comme exposants , mais les a qualifiés de "numéros absurdes".

Aussi récemment que le 18ème siècle , le Swiss mathématicien Leonhard Euler croit que les nombres négatifs étaient supérieures à l'infini , et ce était pratique courante pour ignorer les résultats négatifs retournés par des équations sur l'hypothèse qu'ils étaient de sens, tout comme René Descartes a fait avec des solutions négatives dans un système de coordonnées cartésiennes .

Histoire des nombres rationnels, irrationnels et réels

Histoire des nombres rationnels

Il est probable que la notion de date de nombres fractionnaires la préhistoire. Même le Les anciens Egyptiens ont écrit des textes mathématiques décrivant comment convertir générales fractions dans leur notation spéciale. Mathématiciens grecs et indiens classiques faites des études sur la théorie des nombres rationnels, dans le cadre de l'étude générale de la théorie des nombres . Le plus connu d'entre eux est Éléments d'Euclide , datant à environ 300 BC. Parmi les textes indiens, le plus pertinent est le Sthananga Sutra, qui couvre également la théorie des nombres dans le cadre d'une étude générale des mathématiques.

Le concept de fractions décimales est étroitement liée à la notation lieu de valeur décimale; les deux semblent avoir développé en tandem. Par exemple, il est fréquent que les sutras mathématiques Jain à comprennent les calculs de approximations décimal fraction de PI ou de la racine carrée de deux. De même, les textes mathématiques babyloniennes avaient toujours utilisé fractions sexagésimaux avec une grande fréquence.

Histoire de nombres irrationnels

La première utilisation connue des nombres irrationnels était dans l' Indien Sulba soutras composées entre 800 500 av. Les premières preuves de l'existence de nombres irrationnels est généralement attribuée à Pythagore , plus spécifiquement à la Pythagoricien Hippasus de Métaponte, qui a produit un (géométrique plus probable) la preuve de l'irrationalité de la racine carrée de 2. L'histoire raconte que Hippasus découvert nombres irrationnels en essayant de défendre la racine carrée de 2, comme une fraction. Cependant Pythagore croyait en l'absolu de numéros, et ne pouvait pas accepter l'existence de nombres irrationnels. Il ne pouvait pas infirmer leur existence à travers la logique, mais ses convictions ne serait pas accepter l'existence de nombres irrationnels et donc il condamné à mort Hippasus par noyade.

Le XVIe siècle a vu l'acceptation définitive par les Européens de négatifs , intégrales et fractions numéros. Le XVIIe siècle a vu fractions décimales avec la notation moderne assez généralement utilisé par les mathématiciens. Mais ce ne était pas jusqu'à ce que le XIXe siècle que les irrationnels ont été séparés en pièces algébriques et transcendantes, et une étude scientifique de la théorie des irrationnels a été une fois de plus. Il était resté en sommeil depuis près de Euclid . L'année 1872 a vu la publication des théories de Karl Weierstrass (par son élève Kossak), Heine ( Crelle, 74), Georg Cantor (Annalen, 5), et Richard Dedekind. Méray avait pris en 1869 le même point de départ que Heine, mais la théorie est généralement appelé à l'année 1872. La méthode de Weierstrass a été complètement énoncée par Salvatore Pincherle (1880), et a reçu de Dedekind importance supplémentaire par le travail de l'auteur plus tard (1888) et l'approbation récente par Paul Tannery (1894). Weierstrass, Cantor et Heine fondent leurs théories sur la série infinie, alors que Dedekind fonde son sur l'idée d'un couper (Schnitt) dans le système des nombres réels , en séparant tous les nombres rationnels en deux groupes ayant certaines propriétés caractéristiques. Le sujet a reçu des contributions ultérieures aux mains de Weierstrass, Kronecker (Crelle, 101), et Méray.

Fractions continues, étroitement liés à des nombres irrationnels (et en raison de Cataldi, 1613), ont reçu une attention aux mains de Euler , et à l'ouverture de la dix-neuvième siècle ont été mis en évidence à travers les écrits de Joseph Louis Lagrange . Autres contributions remarquables ont été réalisés par Druckenmüller (1837), Kunze (1857), Lemke (1870), et Günther (1872). Ramus (1855) d'abord connecté le sujet avec les déterminants , résultant, avec les contributions ultérieures de Heine, Möbius, et Günther, dans la théorie de Kettenbruchdeterminanten. Dirichlet également ajouté à la théorie générale, de même que de nombreux contributeurs aux applications de l'objet.

Nombres transcendants et reals

Les premiers résultats concernant les numéros de transcendantales étaient 1761 la preuve de Lambert que π ne peut pas être rationnel, et que e ⁿ est irrationnel si n est rationnel (sauf si n = 0). (La constante e a été mentionnée en premier 1618 travaux de Napier sur logarithmes .) Legendre a étendu cette preuve a montré que π ne est pas la racine carrée d'un nombre rationnel. La recherche des racines de quintique et les équations de degré plus élevé était un développement important, le Théorème d'Abel ( Ruffini 1799, Abel 1824) a montré qu'ils ne pouvaient pas être résolus par radicaux (formule impliquant uniquement des opérations arithmétiques et racines). Par conséquent, il était nécessaire de considérer l'ensemble plus large de nombres algébriques (toutes les solutions aux équations polynomiales). Galois (1832) liée équations polynomiales à la théorie des groupes donnant lieu au domaine de la théorie de Galois .

Même l'ensemble des nombres algébriques ne était pas suffisante et l'ensemble des nombres réels comprend nombres transcendants. L'existence de ce qui a été constituée en Liouville (1844, 1851). Hermite prouvé en 1873 que e est transcendantale et Lindemann a prouvé en 1882 que π est transcendant. Enfin Cantor montre que l'ensemble de tous les nombres réels est indénombrablement infini, mais l'ensemble de tous nombres algébriques est infini dénombrable, donc il ya un nombre infini de indénombrablement nombres transcendants.

Infini

La conception plus ancienne connue de mathématique l'infini apparaît dans la Yajur Veda, qui à un moment donné déclare "si vous retirez une partie de l'infini ou d'ajouter une partie à l'infini, ce qui reste encore est l'infini". Infinity est un sujet populaire d'étude philosophique parmi les Jain mathématiciens circa 400 BC. Ils distinguent cinq types de l'infini: infinies dans une et deux directions, infini dans la zone, infini partout, et infini perpétuellement.

Dans l'Ouest, la notion traditionnelle de l'infini mathématique a été défini par Aristote , qui fait la distinction entre infini actuel et infinité potentielle; le consensus général est que seul ce dernier avait vraie valeur. Galileo s ' Deux nouvelles sciences ont discuté de l'idée de one-to-one correspondance entre ensembles infinis. Mais la prochaine avancée majeure dans la théorie a été faite par Georg Cantor ; en 1895 , il a publié un livre sur sa nouvelle théorie des ensembles , introduisant, entre autres choses, le hypothèse continuum.

Une version moderne de l'infini géométrique est donnée par la géométrie projective, qui introduit "points idéaux à l'infini», un pour chaque direction spatiale. Chaque famille de lignes parallèles dans une direction donnée est postulé à converger vers le point idéal correspondant. Ceci est étroitement lié à l'idée de points de fuite dans dessin en perspective.

Les nombres complexes

La première référence éphémère aux racines carrées de nombres négatifs se est produite dans le travail du mathématicien et inventeur Héron d'Alexandrie dans le 1er siècle après JC, quand il a examiné le volume d'un impossible un tronc de pyramide . Ils sont devenus plus importants lorsque dans le 16ème siècle formules fermé pour les racines des polynômes troisième et quatrième degré ont été découverts par les mathématiciens italiens (voir Niccolo Fontana Tartaglia, Jérôme Cardan). Il est vite rendu compte que ces formules, même si l'on était seulement intéressé par des solutions réelles, parfois nécessaires la manipulation des racines carrées des nombres négatifs.

Ce était doublement troublante, car ils ne ont même pas envisager les nombres négatifs d'être sur la terre ferme à l'époque. Le terme «imaginaire» pour ces quantités a été inventé par René Descartes 1637 et qui devait être dérogatoire (voir nombre imaginaire pour une discussion sur la «réalité» des nombres complexes). Une autre source de confusion est que l'équation

semblait être capricieusement incompatible avec l'identité algébrique

,

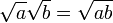qui est valable pour réel positif nombres a et b, et qui a également été utilisé dans les calculs de nombres complexes avec l'un des a, b positif et l'autre négatif. L'utilisation incorrecte de cette identité, et l'identité liées

dans le cas où a et b sont négatifs, même tourmenté Euler . Cette difficulté a conduit par la suite à la convention d'utiliser le symbole spécial i à la place de √-1 pour se prémunir contre cette erreur.

Le 18ème siècle a vu les travaux de Abraham de Moivre et Leonhard Euler . Pour De Moivre est due (1730) la formule bien connue qui porte son nom, la formule de de Moivre:

et à Euler (1748) La formule d'Euler de analyse complexe:

L'existence de nombres complexes ne était pas complètement accepté jusqu'à ce que le interprétation géométrique avait été décrit par Caspar Wessel en 1799 ; il a été redécouvert quelques années plus tard et popularisé par Carl Friedrich Gauss , et par conséquent la théorie des nombres complexes a reçu une expansion notable. L'idée de la représentation graphique des nombres complexes était apparu, cependant, dès 1685, dans Le Tractatus de l'algèbre de Wallis.

Aussi en 1799, Gauss a fourni la première preuve généralement reconnus du théorème fondamental de l'algèbre, montrant que tout polynôme sur les nombres complexes a un ensemble complet de solutions dans ce domaine. L'acceptation générale de la théorie des nombres complexes ne est pas un peu en raison de travaux de Augustin Louis Cauchy et Niels Henrik Abel, et surtout ce dernier, qui était le premier à utiliser hardiment nombres complexes avec un succès qui est bien connu.

Gauss étudié nombres complexes de la forme a + bi, où a et b sont solidaires, ou rationnelle (et i est l'un des deux racines de x ² + 1 = 0). Son élève, Ferdinand Eisenstein, a étudié le type a + bω, où ω est une racine complexe de x ^3-1 = 0. D'autres ces classes (appelé corps cyclotomiques) de nombres complexes sont dérivées de la racines de l'unité x ^k - 1 = 0 pour des valeurs plus élevées de k. Cette généralisation est largement dû à Ernst Kummer, qui a aussi inventé numéros idéales, qui ont été exprimés comme des entités géométriques par Felix Klein en 1893. La théorie générale des champs a été créé par Évariste Galois, qui a étudié les champs générés par les racines de toute équation polynomiale F (x) = 0.

En 1850 Victor Puiseux Alexandre a pris l'étape clé de distinguer entre les pôles et les points de branchement, et introduit le concept de points singuliers essentielles; ce serait éventuellement conduire à la notion de étendue plan complexe.

Nombres premiers

Les nombres premiers ont été étudiés à travers l'histoire enregistrée. Euclid consacré un livre des éléments à la théorie des nombres premiers; en elle il a prouvé l'infinité des nombres premiers et le théorème fondamental de l'arithmétique , et a présenté le Algorithme d'Euclide pour trouver le plus grand commun diviseur des deux nombres.

En 240 BC, Eratosthène a utilisé le Crible d'Ératosthène d'isoler rapidement les nombres premiers. Mais plus la poursuite du développement de la théorie des nombres premiers en Europe remonte à la Renaissance et des époques ultérieures.

En 1796 , Adrien-Marie Legendre conjecturé le théorème des nombres premiers, décrivant la distribution asymptotique des nombres premiers. Autres résultats concernant la répartition des nombres premiers comprennent la preuve de Euler que la somme des inverses des nombres premiers diverge et la conjecture de Goldbach qui prétend que toute assez grand nombre pair est la somme de deux nombres premiers. Une autre hypothèse relative à la répartition des nombres premiers est le Hypothèse de Riemann, formulée par Bernhard Riemann dans 1859 . Le théorème des nombres premiers a finalement été prouvé par Jacques Hadamard et Charles de la Vallée-Poussin en 1896 .