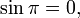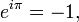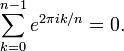L'identité d'Euler

À partir de e ⁰ = 1, se déplaçant à la vitesse i par rapport à sa position pour la durée de π, et en ajoutant 1, on arrive à 0. (Le diagramme est un diagramme d'Argand )

Dans l'analyse mathématique , l'identité d'Euler, nommé d'après Leonhard Euler , est l'équation

où

est Le nombre d'Euler, la base du logarithme naturel,

est l' unité imaginaire , l'un des deux nombres complexes dont le carré est négatif (l'autre est ), Et

est pi , la rapport de la circonférence d'un cercle à son diamètre.

L'identité d'Euler est parfois également appelée l'équation d'Euler.

Nature de l'identité

L'identité d'Euler est considéré par beaucoup d'être remarquable par sa beauté mathématique. Trois de base arithmétiques opérations se déroulent exactement une fois chacun: outre , la multiplication et exponentiation . L'identité relie également cinq fondamentale constantes mathématiques:

• Le numéro 0 .
• Le numéro 1 .
• Le nombre π , qui est omniprésent dans la trigonométrie , géométrie de l'espace euclidien , et l'analyse mathématique .
• Le Numéro e, la base de logarithmes naturels , ce qui est largement répandu dans l'analyse mathématique (e ≈ 2,71828).
• Le nombre i , unité imaginaire des nombres complexes , qui contiennent les racines de tous les polynômes non constants et conduisent à connaissance plus approfondie de nombreux opérateurs, tels que l'intégration .

En outre, dans l'analyse mathématique, les équations sont généralement écrites avec zéro d'un côté.

Perceptions de l'identité

Un sondage mené par lecteur Mathematical Intelligencer nommé l'identité comme le plus beau théorème en mathématiques. Un autre sondage mené par lecteur Physics World en 2004 nommé l'identité d'Euler «la plus grande équation jamais", avec les équations de Maxwell .

Le livre de Dr. Fabulous Formule d'Euler [2006], par Paul Nahin (professeur émérite à l'Université du New Hampshire), est consacré à l'identité d'Euler; ce est 400 pages. Le livre affirme que l'identité définit "l'étalon-or pour la beauté mathématique."

Constance Reid a affirmé que l'identité d'Euler était "le plus célèbre formule dans toutes les mathématiques."

Gauss aurait commenté que si cette formule ne était pas immédiatement apparente à un étudiant sur étant dit il, l'étudiant ne serait jamais un mathématicien de première classe.

Après avoir prouvé l'identité dans une conférence, Benjamin Peirce, un noté XIXe siècle mathématicien et Professeur à Harvard, a déclaré: "Il est absolument paradoxale; nous ne pouvons pas comprendre, et nous ne savons pas ce que cela signifie, mais nous l'avons prouvé, et donc nous savons que ce doit être la vérité."

Stanford professeur de mathématiques Keith Devlin dit, "Comme un sonnet de Shakespeare qui capture l'essence même de l'amour, ou une peinture qui fait ressortir la beauté de la forme humaine qui est beaucoup plus que juste la couleur de peau, l'équation d'Euler descend dans les profondeurs mêmes de l'existence."

Dérivation

La formule d'Euler pour un angle général.

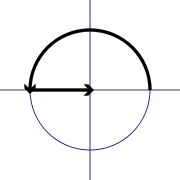
L'identité est un cas particulier de La formule d'Euler de analyse complexe, qui stipule que

pour tout nombre réel x. (Notez que les arguments de la trigonométrique fonctions sin et cos sont prises pour être en radians .) En particulier, si

puis

Depuis

et

il se ensuit que

ce qui donne l'identité

Généralisation

L'identité d'Euler est un cas particulier de l'identité plus générale que la n ième racines de l'unité, pour n> 1, se ajoutent à 0:

L'identité d'Euler est le cas où n = 2.

Attribution

Bien Euler a écrit sur sa formule relative à cos e et les modalités de péché, il ne ya aucune trace connue d'Euler fait déclarant ou dérivant l'équation d'identité simplifiée elle-même; En outre, la formule a probablement connu avant Euler. Ainsi, la question de savoir si ou non l'identité devrait être attribuée à Euler est sans réponse.