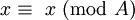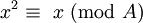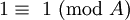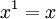Système de numération

Renseignements généraux

Ce contenu de Wikipedia a été sélectionné par SOS Enfants d'aptitude dans les écoles à travers le monde. enfants SOS est le plus grand don de charité du monde enfants orphelins et abandonnés la chance de la vie familiale.

Systèmes de numération par la culture
Chiffres indo-arabes Western Arabe Est Arabe Famille indienne Tamil Telugu Birman Khmer Lao Mongol Thaï Chiffres Asie de l'Est Chinois Japonais Suzhou Coréen Vietnamien Compter tiges Chiffres alphabétiques Abjad Arménien Aryabhata Cyrillique Ge'ez Grecque Géorgien Hébreu D'autres systèmes historiques Égéen Grenier Babylonien Brahmi Égyptien Étrusque Inuits Kharosthî Maya Quipu Romain
Systèmes de positionnement par base
Decimal (10)
1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 20 24 26 27 32 36 60 64 85
Ternaire équilibré
Liste des systèmes de numération

Un système de numération (ou système de numération) est un notation mathématique pour représenter les nombres d'un ensemble donné par des symboles d'une manière cohérente. Il peut être considéré comme le cadre qui permet le chiffre «11» pour être interprété comme le binaire numérique pour trois, le décimal numérique pour onze, ou d'autres numéros dans différents bases.

Idéalement, un système de numération sera:

Représenter un ensemble utile de chiffres (par exemple, tous les nombres entiers, entiers ou des nombres réels )
Donner à chaque nombre représenté une représentation unique (ou au moins une représentation standard)
Refléter la structure algébrique et arithmétique des nombres.

Par exemple, l'habitude décimal représentation des nombres entiers donne à chaque nombre entier d'une représentation unique de finie séquence de chiffres , avec les opérations de l'arithmétique (addition, soustraction, multiplication et division) étant présents sous les standards algorithmes de l'arithmétique. Cependant, lorsque la représentation décimale est utilisé pour les rationnels numéros ou réels, la représentation ne est plus unique: nombres rationnels ont deux chiffres, un standard qui se termine, tels que 2,31, et un autre qui reproduit, tels que 2,309999999 .... Chiffres qui se terminent ne ont pas de chiffres non-zéro après une position donnée. Par exemple, les chiffres comme 2,31 et 2,310 sont prises pour être le même, sauf dans les sciences expérimentales, où une plus grande précision est désigné par la fuite zéro.

Systèmes de numération sont parfois appelés systèmes de numération , mais ce nom est trompeur, car il pourrait se référer à différents systèmes de numéros, tels que le système des nombres réels , le système des nombres complexes , le système de p numéros -adiques, etc. Ces systèmes ne sont pas le sujet de cet article.

Types de systèmes de numération

Le système le plus couramment utilisé de chiffres est connu comme Chiffres indo-arabes, et deux grands mathématiciens indiens pourraient être donnés crédit pour les développer. Aryabhatta de Kusumapura qui a vécu pendant le 5ème siècle développé la notation lieu de la valeur et Brahmagupta un siècle plus tard, introduit le symbole zéro.

Le système numérique plus simple est la Système unaire, dans lequel chaque nombre naturel est représenté par un nombre correspondant de symboles. Si le symbole / est choisi, par exemple, le nombre sept serait représenté par ///////. Tally marques représentent un tel système encore en usage commun. Dans la pratique, le système unaire est normalement utile que pour un petit nombre, bien qu'il joue un rôle important dans informatique théorique. Aussi, Elias codant gamma qui est couramment utilisé dans la compression des données exprime les nombres de taille arbitraire en utilisant unaire pour indiquer la longueur d'un chiffre binaire.

La notation unaire peut être abrégé en introduisant des symboles différents pour certaines nouvelles valeurs. Très souvent, ces valeurs sont des puissances de 10; Ainsi, par exemple, si / se tient pour l'un, - pour les dix et + 100, puis le numéro 304 peut être compacte représentés comme +++ //// et le numéro 123 comme + - - /// sans aucune nécessité de zéro. Cela se appelle signer valeur notation. L'ancien Système égyptien est de ce type, et système romain est une modification de cette idée.

Plus utiles sont encore des systèmes qui utilisent les abréviations spéciales pour des répétitions de symboles; par exemple, en utilisant les neuf premières lettres de notre alphabet pour ces abréviations, avec A permanent pour "une occurrence", B "deux occurrences", et ainsi de suite, nous pourrions alors écrire C + D / pour le nombre 304. Le système de nombre de English est de ce type ("trois cents [et] quatre"), comme le sont ceux de presque tous les autres parlées langues , indépendamment de ce que les systèmes écrite qu'ils ont adopté.

Plus élégant est un système de position, aussi connu comme la notation de valeur de. Encore une fois dans la base de travail 10, on utilise dix chiffres différents 0, ..., 9 et en utilisant la position d'un chiffre pour indiquer la puissance de dix que le chiffre doit être multiplié avec, comme en 304 x 100 = 3 + 0 × 10 + 4 × 1. Notez que zéro , qui ne est pas nécessaire dans les autres systèmes, est d'une importance cruciale ici, afin d'être en mesure de «sauter» une puissance. Le Système de numération indo-arabe, emprunté à l'Inde , est un système de base 10 de position; il est utilisé aujourd'hui dans le monde entier.

Arithmétique est beaucoup plus facile dans les systèmes de position que dans les additifs les précédentes; En outre, les systèmes d'additifs ont besoin d'un nombre potentiellement infini de symboles différents pour les différentes puissances de dix; systèmes de position doivent seulement 10 symboles différents (en supposant qu'il utilise en base 10).

Les chiffres utilisés lors de l'écriture des nombres avec des chiffres ou des symboles peuvent être divisés en deux types qui pourrait être appelé le chiffres arithmétiques et le 0,1,2,3,4,5,6,7,8,9 chiffres géométriques 1,10,100,1000,10000 ... respectivement. Les systèmes signe valeur ne utilisent que les chiffres géométriques et le système de positionnement ne utilisent que les chiffres arithmétiques. Le système de connexion valeur n'a pas besoin des chiffres arithmétiques parce qu'ils sont faits par la répétition (sauf pour le Système ionique), et le système de position n'a pas besoin chiffres géométriques parce qu'elles sont fabriquées par la position. Cependant, la langue parlée utilise à la fois arithmétique et chiffres géométriques.

Dans certaines régions de la science informatique, un système base-modifié k de position est utilisé, appelé numération bijective, avec des chiffres 1, 2, ..., k (k ≥ 1), et zéro étant représenté par la chaîne vide. Cela établit une bijection entre l'ensemble de tous ces chiffres-cordes et l'ensemble des entiers non-négatifs, en évitant la non-unicité causée par les zéros de tête. K la numération de bijective est aussi appelé k notation -adique, à ne pas confondre avec nombres p-adiques. Base 1 bijective le même que unaire.

Les bases utilisées

En informatique

Commutateurs, imité par leurs successeurs électroniques construits à l'origine de tubes à vide et de la technologie moderne de transistors, ne ont que deux états possibles: "ouvert" et "fermé". En substituant ouvert = 1 et fermé = 0 (ou l'inverse), on obtient l'ensemble des chiffres binaires. Cette base 2 système ( binaire ) est la base de ordinateurs numériques. Il est utilisé pour effectuer une arithmétique entière dans les ordinateurs presque toutes numériques; une certaine base 3 exotique ( ternaires) et la base-10 ordinateurs ont également été construites, mais ces dessins ont été jetés au début de l' histoire de matériel informatique .

Modernes ordinateurs utilisent transistors qui représentent deux états avec des tensions soit haute ou basse. La plus petite unité de mémoire pour cet état binaire est appelé bit. Les bits sont agencés en groupes pour aider à la transformation, et pour rendre les nombres binaires plus court et plus facile à gérer pour l'homme. Plus récemment, ces groupes de bits, comme octets et des mots, sont dimensionnés en multiples de quatre. Ainsi base 16 ( hexadécimal ) est couramment utilisé comme raccourci. Base 8 (octal) a également été utilisé à cette fin.

Un ordinateur ne traite pas l'ensemble de ses données numérique. Par exemple, certaines d'entre elles peuvent être traités comme des instructions de programme ou de données comme du texte. Toutefois, l'arithmétique et la logique booléenne constituent des opérations les plus internes. Les nombres entiers sont représentés exactement comme entiers. de nombres réels , permettant valeurs fractionnaires, sont généralement estimés comme nombres à virgule flottante. L'ordinateur utilise différentes méthodes pour faire l'arithmétique de ces deux types de numéros.

Cinq

Un système de base 5 ( quinary) a été utilisé dans de nombreuses cultures pour compter. De toute évidence, il est basé sur le nombre de doigts sur une main humaine. Il peut également être considéré comme un sous-base d'autres bases, telles que la base 10 et la base 60.

Huit

Un système de base 8 ( octal) a été conçu par le Yuki de Californie du Nord, qui a utilisé les espaces entre les doigts pour compter. Zéro à sept sont les seuls chiffres possibles. Il ya aussi des preuves linguistiques qui suggère que l'âge du bronze Proto-Indo Européens (dont la plupart des langues européennes et indiennes descendent) pourrait avoir remplacé un système de base 8 (ou d'un système qui ne pouvait compter jusqu'à 8) avec un système de base 10. La preuve est que le mot pour 9, NEWM, est suggéré par certains pour dériver du mot pour «nouveau», newo-, suggérant que le nombre 9 avait été récemment inventé et appelé le «nouveau numéro '(Mallory & Adams 1997) .

Dix

Le système de base 10 ( décimal ) est le plus couramment utilisé aujourd'hui. On suppose qu'ils seraient issus les humains ont dix doigts. Ces systèmes utilisent souvent une plus grande base superposé. Voir Superbase décimal.

Douze

Base-12 (systèmes duodecimal ou dozenal) ont été très populaires car la multiplication et la division sont plus faciles que dans la base-10, avec l'addition et la soustraction étant tout aussi facile. 12 est une base utile, car il a de nombreux facteurs . Ce est le plus petit multiple de un à quatre et de six. Il ya encore un mot spécial pour "douzaine" et tout comme il ya un mot pour dix ^deux, cent, il ya aussi un mot pour 12 ^2, brut. Base-12 pourrait avoir son origine à partir du nombre de doigts dans les quatre doigts d'une main à l'exclusion du pouce, qui est utilisé comme un pointeur en comptage.

Douze est une unité britannique de mesure commune. Il ya douze pouces à un pied. Avant 1971, en monnaie britannique, il y avait 12 centimes à un shilling. . Mots anglais pour les numéros sont également «base-12 'en ce qu'il est un mot unique pour les chiffres de un à douze, avec« treize »étant le premier mot qui a été formée en combinant les numéros (trois et dix).

Il ya 24 heures par jour, généralement compté jusqu'à 12 jusqu'à midi ( h) et encore une fois jusqu'à minuit ( h), souvent subdivisés par six heures dans le comptage (par exemple en Thaïlande ) ou que les interrupteurs entre l'utilisation de termes tels que «nuit», «matin», «après-midi» et «soir», tandis que d'autres langues utilisent ces termes avec des durées de 3 à 9 heures souvent selon commutateurs à quelques-unes des marques d'intervalle de trois heures.

Multiples de 12 ont été d'usage courant que les unités anglaises de la résolution dans le monde analogique et de l'impression numérique, où 1 point équivaut à 1/72 de pouce et 12 points égale à 1 pica, et comme imprimante résolutions 360, 600, 720, 1200 ou 1440 dpi (points par pouce) sont communs. Il se agit de combinaisons de base 12 et base 10 facteurs: (3 x 12) x 10, 12 x (10 x 5), (6 x 12) x 10, 12 x (10 x 10) et (12 x 12) × 10.

Vingt

La civilisation maya et les autres civilisations de Précolombienne Mésoamérique utilisé base 20 ( vigésimal), éventuellement d'origine à partir du nombre de doigts et les orteils d'une personne. Preuve de systèmes de base de 20 comptage est également disponible dans les langues du centre et de l'ouest Afrique .

Restes possibles d'un système de base 20 existent aussi en français, comme en témoignent les noms des nombres de 60 à 99. Par exemple, soixante-cinq est soixante-cinq (littéralement, «soixante [et] de cinq"), tandis que soixante-dix -cinq est soixante-quinze (littéralement, «soixante [et] quinze"). En outre, pour un nombre compris entre 80 et 99, le nombre des «dizaines colonnes" est exprimé en multiple de vingt (un peu semblable à la manière anglaise archaïque de parler de " scores "). Par exemple, quatre-vingt deux est quatre-vingt-deux (littéralement, quatre vingt [s] [et] deux), tandis que quatre-vingt-est quatre-vingt-douze (littéralement, quatre vingt [s] [et ] douze).

Le Langue irlandaise également utilisé de base 20 dans le passé, vingt être fichid, quarante DHA fhichid, soixante trí fhichid quatre-vingt ceithre fhichid. Un vestige de ce système peut être vu dans le mot moderne pour 40, daoichead.

Chiffres danois affichent une base-20 structure similaire.

Soixante

Base 60 ( sexagésimal) a été utilisé par les Sumériens et leurs successeurs dans la Mésopotamie et survit aujourd'hui dans notre système de temps (d'où la division d'une en 60 heures minutes et une minute en 60 seconde) et dans notre système de mesure angulaire (un degré est divisé en 60 minutes et une minute est divisé en 60 seconde). 60 a également un grand nombre de facteurs, y compris les six premiers numéros de comptage . Base-60 systèmes sont soupçonnés d'avoir son origine par la fusion de base 10 et la base 12-systèmes. Le Calendrier chinois, par exemple, utilise une base-60 Jia-Zi 甲子 système pour désigner ans, chaque année dans le cycle de 60 ans d'être nommé avec deux symboles, la première étant en base 10 (appelé Tian-Gan 天干 ou des tiges céleste) et le deuxième symbole étant base 12 (appelés Di-Zhi 地支 ou branches terrestres). Les deux symboles sont augmentés dans les années successives jusqu'à ce que le premier motif revient 60 ans plus tard. Le deuxième symbole de ce système est également lié à l'animal 12 Système zodiaque chinois. Le système Jia-zi peut également être appliquée à compter les jours, avec une année contenant environ six cycles de 60 jours.

Double base (vingt-cinq)

Beaucoup de systèmes de comptage anciens utilisent 5 comme base primaire, presque sûrement provenant du nombre de doigts sur la main d'une personne. Souvent, ces systèmes sont complétées par une base secondaire, parfois dix, parfois vingt. Dans certaines Langues africaines le mot pour 5 est le même que "la main" ou "coup de poing" ( Diolas langue de la Guinée-Bissau , Banda langue de l'Afrique centrale). Le comptage se poursuit en ajoutant 1, 2, 3, 4 ou à des combinaisons de 5, jusqu'à ce que la base secondaire est atteinte. Dans le cas de vingt ans, ce mot signifie souvent «homme complet». Ce système est appelé quinquavigesimal. Il se trouve dans de nombreuses langues du Soudan région.

noms de base

     1 -   unaire 2 - binaire 3 -   ternaire / ternaire 4 -   quaternaire 5 -   quinary / quinternary 6 -   senaire /   heximal / hexary 7 -   septénaire / septuary 8 -   octal / octonary / octonal / octimal 9 -   Système nonaire / novary / noval 10 - décimal / denier 11 -   undecimal / undenary / unodecimal 12 -   dozenal / duodecimal / duodénaire 13 -   tridecimal /   tredecimal / triodecimal 14 -   tetradecimal / quadrodecimal / quattuordecimal 15 -   pentadecimal / quindecimal 16 - hexadécimal / sexadecimal / sedecimal 17 - septendecimal / heptadecimal 18 - octodecimal / decennoctal 19 - nonadecimal / novodecimal / decennoval 20 -   vigésimal / bigesimal / bidecimal 21 - unovigesimal / unobigesimal 22 - duovigesimal 23 - triovigesimal 24 -   quadrovigesimal / quadriovigesimal 26 -   hexavigesimal / sexavigesimal 27 - 28 heptovigesimal - octovigesimal 29 - 30 novovigesimal -   trigesimal / triogesimal 31 - unotrigesimal (... répétez motif nommer ...) 36 -   hexatridecimal / sexatrigesimal (... de motif de répétition nommer ...) 40 - quadragésimale / quadrigesimal 41 - unoquadragesimal (... motif de répétition nommer ...) 50 - quinquagesimal / pentagesimal 51 - unoquinquagesimal (... répétez motif nommer .. .) 60 -   sexagésimal (... de motif de répétition nommer ...) 64 -   quadrosexagesimal (... motif nommer ...) 70 - septagesimal / heptagesimal 80 - octagesimal / octogesimal 90 - nonagesimal / novagesimal 100 - centimal / centésimale (... motif nommer ...) 110 - 111 decacentimal - unodecacentimal ( ... répétez motif nommer ...) 200 - bicentimal / bicentesimal (... répétez nommer motif ...) 210 - 211 decabicentimal - unodecabicentimal (... motif de répétition nommer ...) 300 - tercentimal / tricentesimal 400 - quattrocentimal / quadricentesimal 500 - quincentimal / pentacentesimal 600 - hexacentimal / hexacentesimal 700 - heptacentimal / heptacentesimal 800 - octacentimal / octocentimal / octacentesimal / octocentesimal 900 - novacentimal / novacentesimal 1000 - 2000 millièmes - bimillesimal (... répétez motif nommer ...) 10000 - decamillesimal

Systèmes de position en détail

Dans un système base-b de position numérique (avec b positif nombre naturel connu sous le nom radix), symboles de base B (ou chiffres) correspondant aux premiers nombres naturels b compris zéro sont utilisés. Pour générer le reste des chiffres, la position du symbole dans la figure est utilisée. Le symbole dans la dernière position a sa propre valeur, et comme il se déplace vers la gauche sa valeur est multipliée par b.

Par exemple, dans le décimal système (base 10), les moyens numériques (4,327 x 10 4 ³⁾ + (3 x 10 ²⁾ + (2 x 10 ¹⁾ + (7 × 10 ^0), en notant que 10 ⁰ = 1 .

En général, si b est la base, nous écrivons un certain nombre dans le système de numération de base b en l'exprimant sous la forme d'un _n b ⁿ + a _{n - 1} b ^{n - 1} + un _{n - 2} b ^{n - 2} +. .. + a ₀ b ⁰ et l'écriture des chiffres énumérés a _n a _{n - 1} a _{n - 2} ... un ₀ dans l'ordre décroissant. Les chiffres sont des nombres naturels entre 0 et b - 1 inclus.

Si un texte (comme celui-ci) discute plusieurs bases, et si ambiguïté, la base (elle-même représentée en base 10) est ajouté en indice à la droite du numéro, comme ceci: _base de nombre. Sauf indication par le contexte, des numéros sans indice sont considérés comme décimal.

En utilisant un point de diviser les chiffres en deux groupes, on peut également écrire des fractions dans le système de position. Par exemple, la base 2 chiffre 1 désigne 10,11 × 2 × ¹ + 0 2 ⁰ + 1 x 2 + 1 x ^{-1 -2} 2 = 2,75.

En général, les numéros dans le système de base de b sont de la forme:

$(A_na_ {n-1} \ cdots a_1a_0.c_1 c_2 C_3 \ cdots) _b = \ sum_ {k = 0} ^ n ^ k + a_kb \ sum_ {k = 1} ^ \ infty c_kb ^ {- k}.$

Le nombre b ^k et b ^{- k} sont les poids des chiffres correspondants. La position k est le logarithme du poids w correspondant, ce est- $k = \ log_ {b} w = \ log_ {b} b ^ k$ . La position la plus élevée utilisée est proche de la ordre de grandeur du nombre.

Le nombre de marques de pointage nécessaires dans le Système unaire pour décrire le poids aurait été w. Dans le système de localisation le nombre de chiffres nécessaires pour décrire ce ne est que $k + 1 =$ $\ Log_ {b} w$ $+ 1$ , Pour $k \ ge 0$ . Par exemple, pour décrire le poids 1000 puis 4 chiffres sont nécessaires, puisque 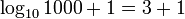$\ Log_ {10} 1000 + 1 = 3 + 1$ . Le nombre de chiffres nécessaire pour décrire la position est $\ Log_ {b} k + 1 = \ log_ {b} \ log_ {b} w + 1$ (En positions 1, 10, 100 ... seulement pour plus de simplicité dans l'exemple décimale).

Position	3	2	1	0	-1	-2	...
Poids	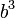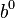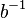$b ^ 3$	$b ^ 2$	$b ^ 1$	$b ^ 0$	$b ^ {- 1}$	$b ^ {- 2}$	...
Chiffre	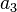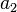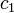$A_3$	$a_2$	$a_1$	$a_0$	$c_1$	$c_2$	...
Exemple décimale poids	1000	100	10	1	0,1	0,01	...
Decimal exemple chiffres	4	3	2	7	0	0	...

Notez que un certain nombre a une expansion de terminaison ou de répéter si et seulement si elle est rationnelle ; Cela ne dépend pas de la base. Un certain nombre qui se termine par une base peut répéter dans un autre (donc 0,3 = ₁₀ ,0100110011001 ... _2). Un nombre irrationnel reste unperiodic (quantité infinie de chiffres unrepeating) dans toutes les bases intégrales. Ainsi, par exemple en base 2, π = 3.1415926 ... ₁₀ peuvent être dépréciés l'unperiodic 11,001001000011111 ... _2.

Si b = p est un nombre premier , on peut définir des numéros de p sous-sols dont l'expansion vers la gauche ne se arrête jamais; On les appelle les nombres p-adiques.

Changement de radix

Un simple algorithme pour convertir des nombres entiers entre bases de numération positive entier est répété division par la racine cible; les restes donnent les "chiffres" à partir de la moins importante. Par exemple, 1020304 base 10 dans la base 7:

 1020304/7 = 145757 r 5
  145757/7 = 20822 r 3
   20822/7 = 2,974 r 4
    2974/7 = 424 r 6
     424/7 = 60 r 4
      60/7 = 8 r 4
       8/7 = 1 r 1
       1/7 = 0 r 1 => 11446435

Par exemple, 10110111 base 2 dans la base 5:

 10110111/101 = 100 100 r 11 (3)
   100100/101 111 r = 1 (1)
      111/101 = 1 r 10 (2)
        1/101 = 0 r 1 (1) => 1213

Pour convertir une "virgule" fraction, faire multiplication répétée, en prenant les parties entières saillantes que les "chiffres". Malheureusement une fraction de terminaison dans une base ne peut résilier dans un autre. Par exemple, la base de 0.1A4C 16 dans la base 9:

 0.1A4C × 9 = 0.ECAC 0.ECAC × 9 = 8.520C 0.520C × 9 = 2.E26C 0.E26C × 9 = 7.F5CC 0.F5CC × 9 = 8.A42C 0.A42C × 9 = 5. C58C => 0,082785 ...

Généralisées entiers de longueur variable

Plus générale est en utilisant une notation (écrit ici little-endian) comme 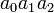$a_0 a_1 a_2$ pour $a_0 + a_1 b_1 + a_2 b_1 b_2$ , Etc.

Il est utilisé dans punycode, un aspect de qui est la représentation d'une séquence d'entiers non négatifs de taille arbitraire sous la forme d'une séquence sans séparateurs, des "chiffres" à partir d'une collection de 36: az et 0-9, 0-25 et représentant 26 à 35 respectivement. Un chiffre inférieur à une valeur de seuil marque que ce est le chiffre le plus significatif, d'où la fin du numéro. La valeur de seuil dépend de la position du nombre. Par exemple, si la valeur de seuil pour le premier chiffre est b (ce est à dire 1) puis un (soit 0) marque la fin du numéro (il a juste un chiffre), donc en nombre de plus d'un chiffre la gamme est seulement b -9 (1-35), donc le poids b ₁ est de 35 au lieu de 36. Supposons que les valeurs de seuil pour les deuxième et troisième chiffres sont c (2), puis le troisième chiffre a un poids 34 × 35 = 1190 et nous avons la séquence suivante:

a (0), ba (1), ca (2), .., 9a (35), bb (36), cb (37), .., 9b (70), BCA (71), .., 99a (1260), bcb (1261), etc.

Notez que contrairement à un 35 système de base numérique régulière, nous avons nombres comme 9b où 9 et B représentent chacun 35; encore la représentation est unique parce que ca et aca ne sont pas autorisés.

La souplesse dans le choix des valeurs de seuil permet d'optimiser en fonction de la fréquence d'occurrence des chiffres de tailles différentes.

Le cas avec tous les valeurs de seuil égal à 1 correspond à bijective numération, où les zéros correspondent à des séparateurs de nombres avec des chiffres qui sont non nulle.

Propriétés des systèmes numériques avec des bases entières

Systèmes de numération avec base A, où A est un entier positif, posséder les propriétés suivantes:

Si A est encore et A / 2 est impair, toutes les puissances entières supérieur à zéro du nombre (A / 2) 1 seront contiennent (A / 2) 1 comme leur dernier chiffre

Si A et A / 2 sont pairs, alors tous les puissances entières supérieure ou égale à zéro du nombre (A / 2) alterne entre 1 comportant (A / 2) +1 et 1 comme dernier chiffre. (Pour puissances impaires il sera (A / 2) 1, même pour les pouvoirs qu'il aura 1)

Preuve de la première propriété:

Définir 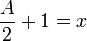${A \ over 2} + 1 = x$ Alors x est pair, et tout $x ^ p$ P supérieur à 0 doit être encore. La propriété est équivalente à

$\! \ X ^ p \ equiv \ x \ (\ mbox {mod} \ A)$

Nous vérifions d'abord le cas pour p = 1

$\! \ X \ equiv \ x \ (\ mbox {mod} \ A)$

x est inférieur à un, donc le résultat est trivial. Nous vérifions ensuite pour p = 2:

$\! \ X ^ 2 = xx$

$\! \ X ^ 2 = x (x-1) + x$

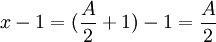Depuis $x-1 = ({A \ over 2} + 1) - 1 = {A \ over 2}$ , Alors pour tout, même N:

$\! \ {NA \ over 2} = N (x-1) \ equiv \ 0 \ (\ mbox {mod} \ A) \ (1)$

Parce que x est pair, alors 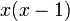$x (x-1)$ est congru à zéro modulo A. Par conséquent:

$\! \ X ^ 2 \ equiv \ x \ (\ mbox {mod} \ A)$

Par induction, en supposant que la propriété est vraie pour p -1:

$\! \ X ^ p = {x ^ {p-1}} = {x x ^ {p-1}} (x-1) + x ^ {p-1}$

Depuis l'affaire tient pour p -1, 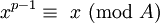${X ^ {p-1}} \ equiv \ x \ (\ mbox {mod} \ A)$ . Depuis

$\! \ {X ^ {p-1}} (x-1)$

est un exemple de l'équation 1, puis ${X ^ {p-1}} (x-1) \ equiv \ 0 \ (\ mbox {mod} \ A)$ . Cela laisse, pour tout p supérieur à 0,

$\! \ X ^ p \ equiv \ x \ (\ mbox {mod} \ A)$

CQFD

Preuve de la deuxième propriété:

Définir 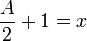${A \ over 2} + 1 = x$ Alors x est impair, et tout $x ^ p$ pour p supérieur ou égal à 0 doit être impair. La propriété est équivalente à

$! \ \ X ^ p \ equiv \ 1 \ (\ mbox {mod} \ A); \ \ mbox {if} \ p \ equiv \ 0 \ (\ mbox {mod} \ 2)$

$! \ \ X ^ p \ equiv \ x \ (\ mbox {mod} \ A); \ \ mbox {if} \ p \ equiv \ 1 \ (\ mbox {mod} \ 2)$

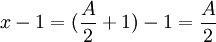Depuis $x-1 = ({A \ over 2} + 1) - 1 = {A \ over 2}$ , Alors pour tout impair E:

$\! \ {EA \ over 2} = E (x-1) \ equiv \ {A \ over 2} \ (\ mbox {mod} \ A) \ (2)$

L'affaire est d'abord vérifié pour p = 0:

$\! \ X ^ 0 = 1$

$\! \ 1 \ equiv \ 1 \ (\ mbox {mod} \ A)$

Ce résultat est trivial

Ensuite, pour p = 1:

$\! \ X ^ 1 = x$

$\! \ X \ equiv \ x \ (\ mbox {mod} \ A)$

Ce résultat est également trivial

Ensuite, pour p = 2:

$\! \ X ^ 2 = x xx = (x-1) + x$

Parce que x est impair, alors x (x-1) est un cas de l'équation 2,

$x (x-1) + x \ equiv \ {{A \ over 2} + x} \ (\ mbox {mod} \ A)$

$\! \ {A \ over 2} + x = {A \ over 2} + {A \ over 2} + 1 = A + 1$

$\! \ A + 1 \ equiv \ 1 \ (\ mbox {mod} \ A), (\ mbox {so} \ x (x-1) + x = x ^ 2 \ equiv \ 1 \ (\ mbox {mod } \ A)$

Ensuite, pour p = 3:

$\! \ X ^ 3 = {x ^ 2} x = {x ^ 2} (x-1) + x ^ 2$

Parce que $x ^ 2$ est impair, ${2} x ^ (x-1) + x ^ 2$ est un cas de l'équation 2,

$\! \ {X} ^ 2 (x-1) + x ^ 2 \ equiv \ {{A \ over 2} + x ^ 2} \ (\ mbox {mod} \ A)$

Depuis $x ^ 2 \ equiv \ 1 \ (\ mbox {mod} \ A)$ ,

$\! \ {X} ^ 2 (x-1) + x ^ 2 \ equiv \ {{A \ over 2} + 1} \ (\ mbox {mod} \ A)$

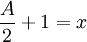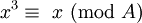${{A \ over 2}} + 1 = x$ Alors $x ^ 3 \ equiv \ x \ (\ mbox {mod} \ A)$ .

Par induction, en supposant que la propriété est vraie pour p -1:

$\! \ X ^ p \ equiv \ {x ^ {p-1}} (x-1) + x ^ {p-1}$

Si p est impair:

$\! \ X ^ {p-1} \ equiv \ 1 \ (\ mbox {mod} \ A)$

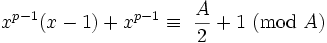Depuis ${X ^ {p-1}} (x-1)$ est un cas de l'équation (2), ${X ^ {p-1}} (x-1) + x ^ {p-1} \ equiv \ {{A \ over 2} + 1} \ (\ mbox {mod} \ A)$ Alors

$x ^ p \ equiv \ x \ (\ mbox {mod} \ A)$

Si p est encore:

$\! \ X ^ {p-1} \ equiv \ x \ (\ mbox {mod} \ A)$

Depuis ${X ^ {p-1}} (x-1)$ est un cas de l'équation (2), ${X ^ {p-1}} (x-1) + x ^ {p-1} \ equiv \ {{A \ over 2} + x} \ (\ mbox {mod} \ A)$ .

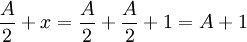
${A \ over 2} + x = {A \ over 2} + {A \ over 2} + 1 = A + 1$

$A + 1 \ equiv \ 1 \ (\ mbox {mod} \ A)$ Alors

$x ^ p \ equiv \ 1 \ (\ mbox {mod} \ A)$